П.Г.Фрик - Турбулентность модели и подходы, часть 2

81

Элементы матриц PNnMm , K NnMm è RNnMmLl зависят от времени, так они зависят от взаимного расположения взаимодействую щ их вихрей, а положения вихрей меняются в соответствии с уравнением (6.22). Энстрофия и энергия системы определяю тся выражениями

Н а этом этапе делается первое сильное предположение, состоящ ее в том, что мы пренебрегаем недиагональностью матриц P , P è K по малому индексу (по больш ому индексу матрицы диагональны в силу способа разбиения пространства волновых векторов). Тогда

83

уравнения при отсутствии диссипативного члена должны сохранять энергию и энстрофию, определенные выражениями (6.33). Для того, чтобы обеспечить сохранение квадратичных величин, нужно чтобы они сохранялись в единичном взаимодействии трех вихрей. П ерепиш ем уравнение (6.34) в виде

тим, что элементы матрицы T зависят только от относительного положения трех вихрей и отнош ения их масш табов (номеров ярусов)

С учетом (6.38) запиш ем условия сохранения энергии и энстрофии, используятолько больш ие индексы матрицы:

седних ярусов с третьим, который отстоит от них через один ярус, и т.д.),

85

СМ -200 фирмы Thinking Machines Corporation, имею щ ем 8192 процессора. Компью тер относится к параллельным системам типа SIMD (Single Instruction Multi Data), допускаю щ им одновременное выполнение всеми процессорами только одной и той же операции. Такие вычислительные системы эффективны только при реш ении задач, в которых требуется одновременное выполнение больш ого числа одинаковых действий с различными данными. Рассматриваемая иерархическая модель как рази относится к таким задачам.

Ðèñ.6.11

Реш алась система для 12 ярусов ( N от 0 до 11), вклю чаю щ ая всего 5592405 вихрей. М оделировался инерционный интервал переноса энстрофии - подкачка осущ ествлялась в первом и втором ярусе, а отвод энергии -

âнулевом.

Âстационарном режиме измерялись интегральные и локальные характеристики полей завихренности и скорости. Н а рис.6.9 показаны осредненные по времени распределения энергии и энстрофии по ярусам. Н аклон графика энергии в инерционном интервале соответствует спектральному

закону E(k) ~ k − 3.3±0.05 . П реимущ ество иерархической модели состоит в том, что она позволяет непосредственно пронаблю дать локальные вариации наклона спектрального закона для плотности энергии. Действительно, локальный наклон спектра можетбыть определен по отнош ению энергии пары вертикальных соседей в иерархическом дереве. Рис.6.10 показывает гистограмму таких локальных наклонов (точнее, на графике показан логарифм отнош ения энергий последовательной пары вихрей в дереве). Разными значками обозначены данные, относящ иеся к различным ярусам. Локальные значения наклона спектра лежат в ш ироком интервале значе- ний, непосредственно подтверждая концепцию мультифрактальной структуры турбулентного потока.

В пределах инерционного интервала точки, относящ иеся к различ- ным ярусам, ложатсяна гистограммах на одну кривую линию, однако, бо-

86

лее тщ ательное исследование свойств распределения вероятности показывает систематическое изменение ее структуры по мере уменьш ения мас- ш табов. В качестве меры отличия распределения вероятности от нормального часто использую т коэффициент эксцесса, определяемый в наш ем слу- чае для каждого яруса, как

Н а рис.6.11 показано изменение во времени коэффициентов эксцесса, вычисляемых для ш естого и восьмого ярусов (оба внутри инерционного интервала). Глядя на рисунок, можно сделать два важных вывода. Вопервых, графики свидетельствую т о сильной временной перемежаемости - в отдельные моменты времени эксцесс растет до значений, равных нескольким сотням. Во-вторых, можно видеть, что коэффициент эксцесса восьмого яруса систематически превышает коэффициент ш естого яруса. Этот факт подтверждает и рис.6.12, на котором показаны средние по времени значения логарифма коэффициентов (6.44) для всех ярусов (точки 1). Виден монотонный ростэксцесса с ростом номера яруса. Это означает, что чем меньш е масш таб, тем больш ие выбросы возникают в функциях распределения вероятности (на гистограммах эти выбросы практически не

видны, так как сливаю тсясосью абсцисс). Н а этом же рисунке для сравнения приведены коэффициенты эксцесса, полученные в каскадной модели двумерной турбулентности. Об этих моделях речь пойдет в последней главе

èтам мы вернемсяк обсуждению этого графика.

Ïоследний рис.6.13 показывает результаты непосредственного вы- числения фрактального спектра f (α ) по алгоритму, описанному в пара-

графе4.5.3. График подтверждаетвыводы, сформулированные при обсуждении мультифрактальных моделей, а именно тот факт, что, являясьпо сути моделью с бесконечным числом параметров, такая модель описывает лю бой спектр. Вид функции f (α ) всегда одинаков. И нтерес в ней представляю т лиш ь несколько точек, например верш ина, абсцисса которой соответствуетсреднему наклону спектра.

88

следовании структуры пространственных полей. Временные ряды представляю тсобой одномерный сигнал и все основные идеи прощ е продемонстрировать на задачах анализа временных последовательностей. П о этой причинемы забудем на некоторое время о пространственных полях и переклю чимсяна сигналы вида f (t) .

П ервая попытка построить функциональный базис, состоящ ий из функций, каждая из которых характеризует пульсации определенной продолжительности в определенный момент времени, принадлежит А.Хаару (1909г.). П ервыесемь функций Хаара, построенные на единичном отрезке, показаны на рис.6.14. Каждая функция представляет собой пару следую - щ их друг за другом прямоугольных импульсов с разными знаками и одинаковой длительностью . Среднее значение любой функции равно нулю , а совокупность функций образует полный ортонормированный базис. Каждая функциястрого локализована в физическом пространстве(во времени), но характеризуетсямедленно спадаю щ им спектром частот (как 1/ν ).

Следую щ им ш агом стали функции Литлвуда - П елли (1937г.). И менно это семейство функций получается при построении одномерного иерархиче- ского базиса. Ф ункции строятся путем вырезания полосы частот в пространстве Ф урье. Это дает строгую локализацию в пространстве частот, но медленное затухание функции в физиче- ском пространстве (во времени): функции описываю т осцилляции, амплитуда которых падаеткак 1/ t .

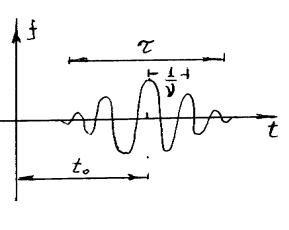
Важным этапом в развитии идеи локального анализа спектральных (частотных) свойств стало преобразование Габора (1946г.), называемое такжефурье-преобразованием в окнах. Ф ункции Габора представляют собой гармонический сигнал, модулированный функцией Гаусса. Они хоро- ш о локализованы и во времени и в частотах, но каждая функция Габора характеризуетсятремя параметрами: положением центра окна t0 , ш ириной

îêíà τ и частотой осцилляций ν (рис.6.15). П ри этом функции различного масш таба не являю тсяподобными (имею т различное число осцилляций).

Вейвлеты объединили в себе два важных свойства - подобие и выраженную локализованность в физическом и фурье-пространствах. Сформулируем требования, которым должно удовлетворять семейство функций, чтобы быть вейвлетами.

1) Допустимость. Ф ункция , которую будем называть анализирую щ им вейвлетом (употребляю т также термин материнский вейвлет), должна иметьнулевое среднее значение:

90

лета зависит от целей проводимого анализа.

П риведем несколько примеров ш ироко используемых вейвлетов. П ростым вещ ественным вейвлетом, ш ироко используемым в задачах, требую щ их хорош его пространственного разреш ения и не требовательных к спектральному разреш ению , является вейвлет, получивш ий название«мексиканская ш ляпа»(рис.6.16,а),

В задачах, требую щ их лучш его спектрального разреш ения, часто используетсявейвлетМ орле - комплексная функция вида

Н а рис.6.16,б сплош ной линией показана его вещ ественная часть, а пунктриной - мнимая. Сама функция (6.49) совпадаетсвидом функций, используемых в преобразовании Габора, но семейство вейвлетов отличается от функций Габора тем, что один раз выбрав частоту ω 0 для анализирую щ его

вейвлета и задав тем самым число осцилляций, мы в дальнейш ем сжимаем или растягиваем функцию как целое, не наруш ая подобия отдельных функций семейства.

6.4.Í епрерывноевейвлет-преобразование

Íепрерывноевейвлет-преобразование одномерной функции f (t) åñòü

ãäå ψ (t) - вещ ественная или комплексная функция, удовлетворяю щ ая требованиям 1-4 раздела 6.4. Если ψ)( ω ) = òψ ( t )e− iωt dt есть фурье-образанализи- рую щ его вейвлета и выполнено условие

то для преобразования (6.50) сущ ествуетформула обращ ения