П.Г.Фрик - Турбулентность модели и подходы, часть 2

21

Следую щ ий ш аг состоит в замене производных по координатам то- чек 1 и 2 на производные по компонентам вектора l . Это оправдывается тем, что всекорреляционные характеристики в однородном потокезависят только от этого вектора. П ри этом ∂1k = − ∂k , à ∂2k = ∂k . П олучаем

∂t bik = ∂ j < v1 j v1i v2k > − ∂ j < v1i v2k v2 j > + 2ν < v1i v2k >

и, окончательно,

В уравнение (4.44) необходимо подставить выражения для тензоров bij ,k (4.43) è bik (4.34). П ри вычислении производной по времени от послед-

него появляется производная по времени от среднего квадрата скорости, которая есть скорость диссипации энергии

Опуская достаточно длинные вычисления, приведем окончательное уравнение

Рассматривая стационарную или, по крайней мере, квазистационарную турбулентность, когда член ∂t Bll все равно много меньш е скорости

диссипации, можно отбросить слагаемое с производной по времени. И н- тегрирование(4.45) по l дает уравнение Колмогорова

Константа интегрирования принята равной нулю в силу требования обращ ения в нуль корреляций при l → ∞ .

Уравнение (4.46), как и уравнение (4.45), вклю чает две независимые корреляционные функции и не является достаточным для их нахождения. П опытка написать дополнительноеуравнение для корреляционного тензора третьего порядка приведет к уравнению , содержащ ему тензор четвертого порядка и т.д. Таким образом, снова возникает проблема замыкания, с которой мы уже сталкивались при рассмотрении уравнений для одното- чечных моментов турбулентных полей.

Уравнение (4.46) справедливо для всех l << L , то есть и для инерционного, и для диссипативного интервалов. В инерционном интервале послед-

22

ним слагаемым, пропорциональным вязкости, можно пренебречь и полу- чить замкнутое уравнение для корреляционной функции третьего порядка

Уравнение (4.47), которое часто называют «законом 4/5», остается одним из важнейш их результатов, полученных для мелкомасш табной турбулентности. Следует ещ е раз подчеркнуть, что закон (4.47) представляет собой точный результат, полученный для инерционного интервала только на основе уравнений Н авье - Стокса. Таким образом, среди оценок (4.22) есть одна, справедливость которой являетсядоказанной, а именно,

S3 (l) ~ εl .

Для всех остальных структурных функций формула (4.22) является лиш ь оценкой, на слабость которой впервые указал Л.Ландау уже в 1942 году. Суть знаменитого замечания Ландау состоит в том, что в правой части формулы стоитскоростьдиссипации энергии ε , которая в действительности не является постоянной, а также представляет собой случайную величину, характеризуемую собственной функцией распределения. В выражение для структурной функции третьего порядка входитсобственно среднее значение скорости диссипации и проблемы среднего значения не возникает. Во всех остальных случаях в оценки входят различные степени слу- чайной величины и, естественно, среднее значение от величины в некоторой степени не есть эта жестепень от среднего.

4.4. Логнормальная модель (К62)

Экспериментальные исследования статистических свойств мелкомас- ш табной турбулентности ведутся, начиная с пятидесятых годов. Н а первых порах основной интерес представляло экспериментальное подтверждение закона «пяти третей» (4.23) и определение входящ ей в него константы. В многочисленных экспериментах было подтверждено сущ ествование инерционного интервала с распределением энергии пульсаций скорости, близким к закону «5/3». И змерения входящ ей в закон константы дали значения C ≈ 1.5 , но интерес к точному измерению этой величины упал после того,

24

руш аю т колмогоровский сценарий однородной турбулентности.

Н аруш ение локальной однородности турбулентности получило название«перемежаемости». Суть этого явления состоит в том, что в турбулентности даже при сколь угодно больш их числах Рейнольдса активные области сосущ ествую тспассивными, в которых течение квазиламинарно.

П ервую попытку скорректировать закон (4.22) путем учета статисти- ческих свойств поля диссипации энергии сделал сам Колмогоров в 1962 году (эту модель будем называть К62).

Для учета структуры поля диссипации энергии Колмогоров ввел в

рассмотрение величину εl , которая представляет собой средню ю скорость

диссипации, измеренную внутри объема с характерным размером l (например, сферы или куба). М одель держитсяна двух дополнительных гипотезах.

П ервая гипотезаэто гипотеза подобия

обобщ аю щ ая формулу (4.22) в том смысле, что теперь в правой части стоит не постоянная величина ε встепени q / 3 , а статистический момент порядка q / 3 , характеризую щ ий структуру случайного поля диссипации энергии на соответствую щ их масш табах l .

Гипотезуподобия (4.50) можно записать в другом виде. Если предположить сущ ествованиестепенных законов вида (4.49) и для моментов поля диссипации, то есть

то гипотеза (4.50) выражается в виде простого соотнош ения между показателями степени в (4.49) и (4.51):

Очевидно, что (4.52) возвращ ает нас к модели К41, если τ q = 0 äëÿ ëþ áûõ q .

Вторая гипотеза К62 касаетсявида функции распределения вероятности для величины εl . Обычно в качестве простейш ей вероятностной модели

рассматриваетсянормальное распределение, однако, в наш ем случае оно не годится, так как диссипация - величина сугубо положительная, а хвост нормального распределения уходит в область отрицательных значений. Колмогоров предложил избежать эту трудность путем рассмотрения логнормального распределения (по нормальному закону распределен логарифм диссипации энергии)

26

В отличие от второй гипотезы, гипотеза подобия (4.50) используется до настоящ его времени, хотя ее интерпретация претерпела сущ ественные изменения. Дело в том, что в формулировке(4.50) эта гипотезанесетвсебе два противоречия. Во-первых, левая часть выражения содержит величину, относящ ую ся к инерционному интервалу, а правая - величину, эффективную только в диссипативном. Во-вторых, диссипацияэнергии есть величи- на сугубо положительная, а пульсации скорости - нет. В таком случае трудно рассчитывать, что статистические свойства этих величин одинаковы, а именно в этом и состоит суть гипотезы подобия.

И збежать отмеченных противоречий можно следую щ им образом. Выделим в пространстве, занятом турбулентным течением, произвольный объем с характерным размером l и рассмотрим изменения плотности энергии пульсаций скорости в этом объеме:

Здесь εl есть диссипацияэнергии за единицу времени на единицу массы, ql - приток энергии за счет работы внеш них сил (такжеза единицу вре-

мени и на единицу массы). П ервое слагаемое в правой части, обозначенное как ηl , описывает приток энергии в выделенный объем через его поверх-

ность.

И зскорости диссипации энергии можно выделить ее среднее значение εl = ε + εl . Если рассматривается стационарно возбуждаемая турбулент-

ность, то средняя скорость диссипации должна быть равна плотности притока энергии за счет внеш них сил, т.е. ql = ε . Тогда

то есть изменения энергии в выделенном объеме определяются потоком энергии через его поверхность и вариациями диссипации. И збежать отме- ченных выше противоречий можно путем рассмотрения не скорости диссипации энергии в объемезаданного масш таба, а потоков энергии через поверхность этого объема. П оследний определяется действием нелинейного

27

члена в уравнении Н авьеСтокса, то есть именно того члена, который определяет нелинейную динамику потока при больш их числах Рейнольдса.

И менно величина ηl и будетиспользована в дальнейш ем как характе-

ристика потоков энергии на различных масш табах движения. Н еобходимо отметить, что переход от использования εl ê ηl произош ел совсем недавно,

а традиция применения в моделях мелкомасш табной турбулентности скорости диссипации энергии столь крепка, что часто даже в работах, где реально пользуются величиной ηl , авторы, тем неменее, используют термин

«скоростьдиссипации энергии».

4.5. Ф ракталы и турбулентность

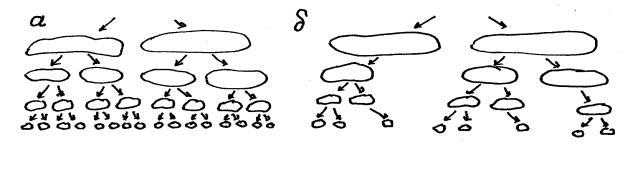
Колмогоровская модель однородной турбулентности (К41) подразумевает равномерное заполнение пространства вихрями каждого масш таба. Такую структуру турбулентности иллюстрирует рис.4.6,а, на котором схематически изображен каскад энергии от вихрей больш его масш таба к вихрям меньш его масш таба и для простоты представлена ситуация, когда каждый вихрь данного масш таба имеет под собой два вихря меньш его. П ри этом вихри каждого масш таба занимают всепространство (на рисунке оно одномерно).

И ная картина соответствует турбулентности с перемежаемостью (рис.4.6,б). В рамках аналогичной схемы в этом случае часть вихрей не получает энергию от вихрей верхнего уровня. Н а следую щ ем уровнеэнергия оставш ихся(активных) вихрей вновь передается только части вихрей и так далее. В результате в пространстве образуется многомасш табная система активных и пассивных областей, которая по построению представляет собой фрактальное множество (см. п.2.6 части 1).

Ðèñ.4.6

И дея использования фракталов для описания структуры поля диссипации энергии впервые была высказана в работе Н овикова и Стью арта в

28

1964ã.2 П ростейш ая динамическая модель инерционного интервала, приводящ ая к фракталам, предложена в работе3. Эта модель, названная авторами β -моделью , описана в следую щ ем параграфе.

Ф ракталы принесли в теорию турбулентности ещ е одну важную идею - идею о неоднозначности масш табных показателей, иначе говоря, идею о сосущ ествовании в развитых турбулентных полях подмножеств с различными законами масш табного подобия (скейлинга).

Н апомним, что уравнения Н авье - Стокса подчиняю тся ш ести принципам инвариантности, то есть, допускаю т ш есть видов преобразований, при которых лю бое реш ение уравнений v(r , t) остается реш ением этих уравнений:

1)пространственный сдвиг,

2)сдвиг по времени,

3)преобразование Галилея,

4)четность,

5)âðàù åíèå,

6)масш табная инвариантность(скейлинг).

П оследнее свойство означает, что уравнения Н авье - Стокса инвариантны к преобразованию

t, r , v a λ1+ α t, λr , λ− α v .

Действительно, такое преобразование приводит к появлению в уравнении движения следую щ их множителей

П ри конечной вязкости инвариантность (подобие) обеспечивается единственно возможным реш ением α = 1, эквивалентным требованию постоянства числа Рейнольдса (во сколько раз увеличивается масш таб, во столько же раз должна быть уменьш ена скорость). Однако, при ν → 0 мас- ш табное подобие обеспечивается лю бым α . Ê41 äàåò ðåø åíèå α = 1/ 3 , монофрактальная модель типа β -модели приводит к другому, но такжеединственному, реш ению . Бифрактальная модель (параграф 4.5.2) предполагает сосущ ествования в потоке двух подмножеств с различными законами подобия (различными α ), а мультифрактальная модель (параграф 4.5.3) рассматриваетнепрерывную последовательность таких подмножеств, приводя к понятию мультифрактального спектра.

2Н овиков Е.А., Стьюарт Р.В. П еремежаемость турбулентности и спектр диссипации энергии // È çâ.ÀÍ

СССР: Серия геофизическая. 1964. N.3. C.408-413.

3Frisch U., Sulem P.-L., Nelkin M. A simple dynamic model of intermittent fully developed turbulence // J.Fluid Mechanics. 1978. Vol.87. P.719-736.

29

4.5.1. β -модель

Обратимсяк турбулентности в кубической области и рассмотрим последовательность масш табов

ln = l0 2− n .

Н а каждом масш табе n исходная область разбивается на кубики с ребром ln , общ еечисло которых есть N = (l0 / ln )3 = 23n .

Следуя схеме рис.4.6,б, будем считать, что при переходе к каждому следую щ ему масш табу активной остается только заданная часть кубиков β , причем эта часть есть величина постоянная, являю щ аяся параметром модели. Двумерная картинка, соответствую щ ая такому построению с

β= 3 / 4 , представлена на рис.4.7.

Íà ìàñø òàáå n число активных вихрей есть M = Nβn , ãäå

à D есть фрактальная размерность активной области. Величина d = 3 - D , равная разности размерности пространства и размерности фрактального множества, называется коразмерностью и просто связана с параметром β :

Рассмотрим теперь каскад энергии в такой модели. Характерное зна- чение пульсации скорости на масш табе ln обозначим как δvn . Тогда харак-

терное время (время оборота вихря соответствую щ его масш таба) есть tn ~ ln / δvn . П ри сплош ном заполнении пространства (случай однородной

турбулентности) плотностьэнергии пульсаций масш таба n

а скоростьпереноса энергии через данный масш таб есть

30

Тогда из гипотезы постоянства потока энергии в любом масш табе, относящ емсяк инерционному интервалу,

немедленно получаетсяколмогоровское выражение

 β - модели энергия данного масш таба сосредоточена только в активной части потока и средняя плотность энергии на этом масш табе равна

Гипотеза (4.61) остается в силе - поток энергии по-прежнему постоянен, но, по мере движения к малым масш табам, он сосредотачивается все в меньш ей части пространства. Следовательно,

Очевидно, что фрактальная размерность D не может быть меньш е двух, так как в этом случае интенсивность пульсаций скорости будет нарастать с уменьш ением масш табов.

П олучим теперь оценку для структурных функций произвольного порядка. И меем