
Краткий курс математического анализа. Том 1
.pdf§ 16. Векторные функции |
217 |
Из формулы (16.23) аналогично случаю скалярных функций вытекает инвариантность записи дифференциала векторной функции:
как для зависимой переменной t, так и для независимой τ |
имеем |
dr = rt dt, dr = rτ dτ , |
(16.26) |
т. е. чтобы из второй формулы получить первую, надо подставить во вторую формулу rτ = rt · tτ и заметить, что tτ dτ = dt.
V. Для производных вектор-функций имеют место формулы, аналогичные соответствующим формулам для скалярных функций:
(r1 + r2) = r1 + r2, (f r) = f r + f r ,
(r1r2) = r1r2 + r1r2,
(r1 × r2) = r1 × r2 + r1 × r2.
Здесь все производные берутся в одной и той же точке. Предполагается, что производные, стоящие в правой части каждого равенства, существуют, и утверждается, что в этом случае существуют и производные, находящиеся в левых частях равенств.
Доказываются эти формулы аналогично скалярному случаю. Докажем, например, последнюю из них.
|
Заметив, что r1(t0 + |
t) = r1(t0) + |
r1, |
r2(t0 + |
|
t) = r2(t0) + |
r2, |
||||||||||||||||||||||||||
получим |
= |
|
t→0 |
|
|
× |
|
|
|
|
− |
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(r1 |
× |
2 |
|
t=t0 |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
r |
) |
= lim0 |
lim |
r1(t0 |
+ |
t) |
|
r2(t0 |
+ |
|
t) |
|
r1(t0) |
|
|
r2(t0) |
= |
|
|
|
|
||||||||||
|
|
|
|
× |
|
|
|
|
|
− |
|
|
|
|
× |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|||||||
|
|
|
|
|
|
(r1(t0) + r1) |
|
(r2(t0) + r2) |
|
r1(t0) |
|
|
r2(t0) |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
t→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t × r2(t0) + r1(t0) × |
|
t |
+ t × r2 = |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
= |
t→0 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
lim |
|
r1 |
|
|
|
|
|
|
|
r2 |
|
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= r |
(t |
) |
× |
r |
(t |
) + r |
|
(t |
) |
× |
r |
(t |
). |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
2 |
0 |
|
|
|
1 |
0 |
|
|
2 |
0 |
|
|||||||
Для дальнейшего нам будет полезна следующая
Ле м м а. Если вектор-функция r(t) дифференцируема в точке t0
ивсе векторы r(t) имеют одну и ту же длину в некоторой окрестности точки t0, то производная r (t0) ортогональна вектору r(t0):
r (t0)r(t0) = 0. |
(16.27) |
Действительно, если в указанной окрестности |r(t)| = c, где c — константа, то |r|2 = c2, т. е. r2 = c. Дифференцируя это равенство, получим 2rr = 0, что равносильно равенству (16.27).
Утверждение леммы содержательно лишь в случае, когда r (t0) = = 0 (если r (t0) = 0, то условие (16.27), очевидно, выполняется и без условия постоянства длины вектора r(t)). В этом случае физический смысл формулы (16.27) состоит в том, что у материальной точки,

218 Гл. 1. Дифференциальное исчисление функций одной переменной
движущейся по поверхности шара (r(t) — радиус-вектор этой точки, t — время движения, c — радиус указанного шара), скорость v = drdt всегда направлена при v = 0 по касательной к поверхности шара, т. е. перпендикулярно радиусу шара.
Производные высших порядков для вектор-функции определяются по индукции: если у вектор-функции r(t) в некоторой окрестности точки t0 задана производная r(n)(t) порядка n, n = 0, 1, 2, ...
(r(0)(t) def= r(t)), то производная порядка n + 1 в этой точке (если эта производная, конечно, существует) определяется по формуле
(n)(t)) .
t=t0
Если векторная функция имеет в некоторой точке n производных, то говорят также, что она в этой точке n раз дифференцируема. Можно
и для векторных функций по аналогии со скалярными ввести понятие дифференциалов высших порядков, но не будем на этом останавливаться.
Если векторная функция r(t) = (x(t), y(t), z(t)) n раз дифференцируема в точке t = t0, то в некоторой окрестности этой точки для функции r(t) имеет место формула
|
n |
|
|
|
|
|
|
|
r(k)(t |
) |
|
|
|
r = r(t0 + t) − r(t0) = |
|
|
0 |
|
tk + o(Δtn), |
Δt → 0, |
k=1 |
k! |
|
|
|||
|
|
|
|
|
|
|
называемая по аналогии со скалярным случаем формулой Тейлора
(порядка n) функции r(t) с остаточным членом в виде Пеано. Эта формула непосредственно следует из разложений по формуле Тейлора координат x(t), y(t), z(t) векторной функции r(t).
Из всего сказанного видно, что рассмотренные определения и утверждения для векторных функций получаются перенесением соответствующих определений и утверждений из теории скалярных функций.
З а м е ч а н и е 3. Следует, однако, иметь в виду, что не все, что справедливо для скалярных функций, имеет прямой аналог в векторном случае. Это относится, например, к теореме Ролля, а следовательно, и к теореме Лагранжа, частным случаем которой является теорема Ролля.
В самом деле, рассмотрим дифференцируемую векторную функцию r(t) = (cos t, sin t), 0 t 2π (третья координата функции r(t) — тождественный нуль). Поскольку r (t) = (− sin t, cos t), то |r (t)| =
= sin2 t + cos2 t = 1 при любом t [0, 2π], и, следовательно, не суще-
ствует такой точки ξ [0, 2π], для которой было бы r (ξ) = 0, несмотря на то, что r(0) = r(2π).
§ 16. Векторные функции |
219 |
Для векторных функций вместо прямого аналога теоремы Лагранжа можно доказать нижеследующую теорему 1.
Ее формулировке и доказательству предпошлем два замечания. З а м е ч а н и е 4. Если вектор x ненулевой и x0 — единичный
вектор в направлении вектора x, т. е. x0 = x/|x|, то
|
|
|
|x| = xx0. |
(16.28) |
||||
В самом деле, согласно определению скалярного произведения |
||||||||
| |
xx0 = |x||x0| cos xx0. |
(16.29) |
||||||
0| |
= 1, |
а |
0 |
|
|
0 |
= 1, |
|
Здесь по условию x |
|
|
|
|
||||
|
xx |
|
= 0 и, следовательно, cos xx |
|
||||
т. е. равенство (16.29) превращается в равенство (16.28).
З а м е ч а н и е 5. Для любых векторов x и y имеет место нера-
венство |
xy |
|x||y|. |
(16.30) |
|
Действительно, |
||||
|
|
|
||
xy |xy| = ||x||y| cos xy| = |x||y| | cos xy| |x||y|. |
|
|||
Те о р е м а 1. Если |
вектор-функция r(t) непрерывна на отрез- |
|||
|
|
|
||
ке [a, b] и дифференцируема внутри него, то существует такая точка ξ (a, b), что
Если r(a) = r(b), то неравенство (16.31) справедливо при любом выборе точки ξ (a, b), так как его левая часть обращается в нуль.
Пусть r(a) = r(b) и, следовательно, r(b) − r(a) = 0. Если e — единичный вектор в направлении вектора r(b) − r(a), то согласно замечанию 4
|r(b) − r(a)| = (r(b) − r(a))e = r(b)e − r(a)e,
т. е. получилась разность значений скалярной функции
f (t) |
def |
(16.32) |
= r(t)e |
||
на концах отрезка [a, b]: |
|
|
|r(b) − r(a)| = f (b) − f (a). |
(16.33) |
|
Из формулы (16.32) следует, что функция f непрерывна на отрезке [a, b] и дифференцируема во всех его внутренних точках, ибо согласно условиям теоремы этими свойствами обладает функция r(t).
Поэтому в силу формулы конечных приращений Лагранжа существует такая точка ξ (a, b), что f (b) − f (a) = f (ξ)(b − a). Но со-
гласно правилу дифференцирования скалярного произведения имеем f (t) = r (t)e, вследствие чего
f (b) |
− |
f (a) = r (ξ)e(b |
− |
a), a < ξ < b. |
(16.34) |
|
|
|
|

220 Гл. 1. Дифференциальное исчисление функций одной переменной
Поскольку в силу неравенства (16.30) имеет место неравенство
то |
|
|
|
|
r (ξ)e |r (ξ)||e| = |r (ξ)|, |
|
(16.35) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
r(b) |
− |
r(a) |
| |
= f (b) |
− |
f (a) |
(16.34) | |
r (ξ) (b |
− |
a), |
a < ξ < b. |
|
|
(16.33) |
|
| |
|
|
||||||
|
|
|
|
|
|
|
|
(16.35) |
|
|
|
|
Неравенство (16.31) доказано.
§17. Длина кривой
17.1.Понятие кривой. Рассмотрим отображение некоторого отрезка [a, b] числовой прямой R в пространство R3, т. е. такое отображение, которое каждой точке t [a, b] ставит в соответствие
точку M (t) пространства R3. Если в пространстве R3 задана прямоугольная декартова система координат x, y, z, то между точками пространства R3 и тройками чисел x, y, z имеется взаимно однозначное соответствие, а поэтому задание отображения M (t) R3, t [a, b],
равносильно заданию трех числовых функций (называемых координатными) x(t), y(t), z(t), где x(t), y(t) и z(t) являются координатами
точки M (t).
Отображение M (t) R3, t [a, b], называется непрерывным на отрезке [a, b], если на этом отрезке непрерывны все его координатные
функции x(t), y(t), z(t).
О п р е д е л е н и е 1. Непрерывное отображение отрезка в пространство называется кривой или, более подробно, параметрически заданной кривой.
Кривые будем обозначать большими греческими буквами Γ, Λ. Если M (t), a t b, — непрерывное отображение какого-либо отрезка [a, b] в пространство, т. е. кривая Γ, то будем писать
Γ = {M (t) ; a t b}, |
(17.1) |
или |
(17.2) |
Γ = {x(t), y(t), z(t); a t b}, |
|
где x(t), y(t), z(t) — координатные функции отображения |
M (t), |
a t b. |
|
Координатные функции x(t), y(t), z(t) отображения M (t), t [a, b], однозначно задают вектор-функцию r(t), координатами которой они
являются: |
(17.3) |
r(t) = (x(t), y(t), z(t)), a t b. |
Эта вектор-функция называется векторным представлением кривой (17.1). Если вектор r(t) является радиусом-вектором с началом в начале координат, то его концом будет точка M (t). В дальнейшем,
§ 17. Длина кривой |
221 |
когда будут рассматриваться векторные представления (17.4) кривой Γ, всегда будет предполагаться, что вектор r(t) является радиу- сом-вектором с началом в начале координат, т. е. что r(t) = OM (t).
При задании кривой Γ ее векторным представлением (17.3) пишут
Γ = {r(t); a t b}. |
(17.4) |
Множество точек пространства R3, на которое отображение (17.1) отображает отрезок [a, b], называется носителем кривой Γ.
Иногда там, где это не может привести к недоразумению, носитель кривой называется также кривой.
Если O — начало координат в пространстве R3, то конец радиусавектора r(t) = OM (t) при изменении параметра t на отрезке [a, b]
пробегает носитель кривой Γ.
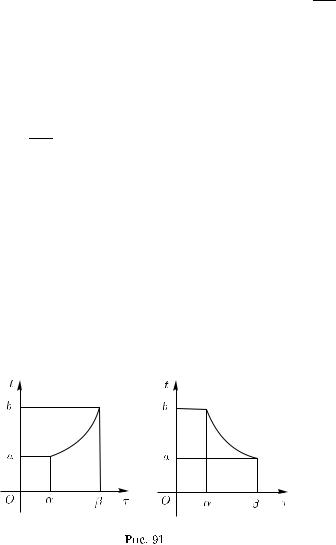
Переменная t называется параметром на кривой Γ. Всякая строго монотонная непрерывная на некотором отрезке [α, β] функция
t = t(τ ), α τ β, |
(17.5) |
отображающая отрезок [α, β] на отрезок [a, b], для которой, следовательно, в случае ее строгого возрастания выполняется условие
t(α) = a, t(β) = b,
а в случае строгого убывания — условие
t(α) = b, t(β) = a
(рис. 91), называется преобразованием параметра t кривой (17.1) (или, полнее, допустимым преобразованием параметра t к парамет-
ру τ ). Обратная к функции t = t(τ ) функция τ = τ (t) является, очевидно, преобразованием параметра для кривой {M (t(τ )); α τ β}.
При преобразовании параметра t = t(τ ) из равенства M (t) = = M (t(τ )), α τ β, следует, что исходная кривая и кривая, получающаяся из нее с помощью преобразования параметра, имеют один и тот же носитель.

222 Гл. 1. Дифференциальное исчисление функций одной переменной
Если t = t(τ ), α τ β, — преобразование параметра, то кривые {M (t) : a t b} и {M (t(τ )) : α τ β} часто называют одной
и той же кривой с разными параметризациями. Таким образом, можно сказать, что кривая — это класс параметрически заданных кривых, связанных допустимыми преобразованиями параметров.
Если координатные функции x(t), y(t), z(t) отображения (17.1) n раз дифференцируемы или n раз непрерывно дифференцируемы (т. е.
имеют n непрерывных производных) на отрезке [a, b], то кривая Γ называется n раз дифференцируемой или, соответственно, n раз непрерывно дифференцируемой кривой.
Преобразованиями параметра n раз (непрерывно) дифференцируемой кривой называются такие n раз (непрерывно) дифференци-
руемые строго монотонные функции (17.5), у которых во всех точках отрезка [α, β] их производная не равна нулю:
t (τ ) = 0, τ |
|
[α, β]. |
|
|
Это условие нужно для того, чтобы обратная функция τ = τ (t), a t b, была также преобразованием параметра τ кривой M (t(τ )), α τ β (см. формулы для производных обратной функции в пп. 1.10.6 и 1.11.2).
Для того чтобы кривая Γ была n раз дифференцируема (соответственно n раз непрерывно дифференцируема, n = 1, 2, ...), необходимо и достаточно, чтобы ее векторное представление (17.2) было n раз дифференцируемо (соответственно n раз непрерывно дифференцируемо). Это следует из того, что непрерывность (дифференцируемость) векторной функции равносильна непрерывности (дифференцируемости) ее координат (п. 16.2).
Точка носителя кривой Γ, в которую при отображении (17.1) отоб-
ражаются по крайней мере две разные точки отрезка [a, b], называется
кратной точкой носителя этой кривой или точкой самопересечений кривой. Если кратная точка носителя кривой Γ имеет в точ-
ности n прообразов при отображении M (t), a t b, то эта точка называется n-кратной.
Если носитель кривой Γ не имеет кратных точек, т. е. отображение (17.1) взаимно однозначно отображает отрезок [a, b] в простран-
ство R3, то кривая Γ называется простой дугой. |
|
R3, |
|||
Точкой кривой |
|
3 |
|
||
|
(17.1) называется пара (M , t), где M = M (t) |
|
|||
a t [a, b]. Точка M R |
|
называется носителем точки (M , t). |
|
|
|
Носитель точки кривой там, где это не может привести к недора-
зумению, называется иногда также точкой кривой.
Если M0 = M (a), а M1 = M (b), то точка (M0, a) называется началом кривой Γ, а точка (M1, b) — ее концом (впрочем, иногда обе точки
(M0, a) и (M1, b) называют концами кривой Γ). Если носители начала
§ 17. Длина кривой |
223 |
и конца кривой Γ совпадают: M (a) = M (b), то кривая Γ называется
замкнутой.
Если у носителя замкнутой кривой нет других кратных точек,
кроме носителя ее начала и конца, который является двукратной точкой, то кривая Γ называется простым замкнутым контуром.
Там, где это не может привести к недоразумениям (например, для простых дуг), точка (M , t) кривой Γ часто обозначается M (t), т. е. тем же символом, что и носитель указанной точки.
Если t1 [a, b], t2 [a, b], t1 < t2, то кривая {M (t); t1 t t2}
называется частью кривой (17.1) или ее дугой
( ) ( )
M t1 M t2
с началом в точке M (t1) и концом в M (t2).
Если носитель кривой Γ лежит в некоторой плоскости, то эта кривая называется плоской.
П р и м е р ы. 1. Рассмотрим две замкнутые плоские кривые:
x = cos t, y = sin t, |
0 t 2π, |
(17.6) |
и |
0 t 4π. |
(17.7) |
x = cos t, y = sin t, |
Их носителями является одна и та же окружность x2 + y2 = 1, но это две разные кривые: у кривой (17.6) параметр t изменяется от 0 до 2π, и эта окружность проходится один раз, а у кривой (17.7) параметр t изменяется от 0 до 4π, и та же окружность проходится два раза.
Носитель кривой (17.6) имеет только одну кратную точку — носитель начала и конца этой кривой. У носителя кривой (17.7) все точки кратные.
2. Непрерывная на некотором отрезке [a, b] функция y = f (x), a x b, задает плоскую кривую x = t, y = f (t), a b, являющуюся, очевидно, простой дугой. Ее носителем является график функции f , а параметром — переменная x. В этом случае пишут
Γ= {y = f (x); a x b}
иговорят, что кривая Γ имеет явное представление — функцию f.
Упорядоченность точек отрезка [a, b] порождает с помощью отоб-
ражения M (t), a t b, упорядоченность точек на кривой Γ =
= {M (t); a t b}. Если t1 < t2, то точка M (t1) кривой Γ называется точкой, предшествующей точке M (t2) этой кривой. Этот порядок
точек называется ориентацией кривой, а кривая, на которой задана ориентация, называется ориентированной кривой.
Порядок точек на кривой |
|
{M (a + b − t) ; a t b} |
(17.8) |

224 Гл. 1. Дифференциальное исчисление функций одной переменной
называется противоположным порядку точек кривой Γ{M (t); a t b} (противоположной ориентацией кривой), а сама кривая (17.8) — кривой, ориентированной противоположно к данной
кривой Γ.
Для ориентированной кривой преобразованием параметра называются только строго возрастающие функции — они не меняют порядок точек, в то время как строго убывающие меняют их порядок на противоположный.
З а м е ч а н и е 1. Задания кривой Γ в виде M (t), (x(t), y(t), z(t))
и r(t), a t b, называют ее параметрическими заданиями, а саму кривую Γ называют также параметрически заданной непрерывной
кривой.
З а м е ч а н и е 2. Если для плоской кривой Γ существует такая функция F (x, y), что координаты всех точек (x, y) носителя кривой Γ
удовлетворяют условию |
(17.9) |
F (x, y) = 0, |
то говорят, что уравнение (17.9) является неявным заданием кривой Γ. Следует иметь в виду, что, вообще говоря, множество всех точек, удовлетворяющих уравнению вида (17.9), не является носителем некоторой кривой в определенном выше смысле даже для достаточно «хороших» функций F (x, y). Например, множество точек, координаты
которых удовлетворяют уравнению
(x2 + y2)(x2 + y2 − 1) = 0,
представляет собой окружность x2 + y2 = 1 и точку (0, 0).
З а м е ч а н и е 3. В случае кривых, лежащих на плоскости, иногда бывает удобно их задавать в полярных координатах ρ, ϕ (ρ — полярный радиус точки плоскости, а ϕ — угол, образованный им с полярной осью), которые связаны с декартовыми координатами x, y
соотношениями |
(17.10) |
x = ρ cos ϕ, y = ρ sin ϕ. |
|
В полярных координатах кривая задается уравнениями вида |
|
ρ = ρ(ϕ), α ϕ β. |
(17.11) |
С помощью формул (17.10) задание кривой уравнением (17.11) сразу сводится к ее параметрическому заданию
x = ρ(ϕ) cos ϕ, y = ρ(ϕ) sin ϕ, α ϕ β,
где за параметр взят полярный угол ϕ.
З а м е ч а н и е 4. Отметим еще, что сформулированное определение кривой не охватывает все то, что интуитивно естественно отнести к понятию кривой, например, прямую линию, гиперболу, параболу и т. п. Чтобы охватить определением и подобные «кривые», следует

226 Гл. 1. Дифференциальное исчисление функций одной переменной
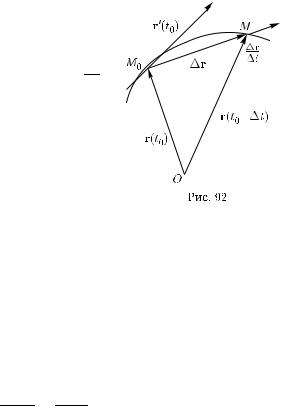
Из сказанного выше следует, что геометрический смысл производной r (t) вектор-функции r(t) состоит в том, что в неособой точке вектор r (t0) направлен по касательной к кривой в конце
радиуса-вектора r(t0). В этом случае вектор r (t0) называется вектором, касательным к кривой в соответствующей точке.
Если r (t0) = ... = r(n−1)(t0) = 0, а r(n)(t0) = 0, то по формуле
Тейлора |
|
|
|
|
|
r(n)(t ) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
r = |
|
|
0 |
|
|
tn + o(Δtn). |
|
|
|
|
(17.14) |
|||||
|
|
|
|
|
n! |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вектор |
r/ tn направлен по секущей M0M , где, как и раньше, |
||||||||||||||||||||
M0 = M (t0), |
M = M (t0 + t), |
а |
|
n! lim |
rn = r(n)(t0). |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t→ |
|
|
|
|
|
|
|
||
Определяя и в этом случае касательную к кривой Γ в точке M0 как |
|||||||||||||||||||||
предельное положение секущих |
M |
M |
при |
t |
→ |
0, |
|
е. как прямую, |
|||||||||||||
0 |
|
|
|
|
т.(n) |
(t0), получим |
|||||||||||||||
проходящую через точку M0 в направлении вектора r |
|
||||||||||||||||||||
ее уравнение в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ρ(τ ) = r(t0) + r(n)(t0)τ , −∞ < τ < +∞. |
|
(17.15) |
||||||||||||||||||
З а м е ч а н и е |
|
1. |
Если рассматривается плоская кривая r(t) = |
||||||||||||||||||
= (x(t), y(t)), |
a |
|
t |
|
|
0 |
|
|
|
|
то уравнение (17.14) касательной |
||||||||||
|
|
b, и r (t |
) = 0, |
||||||||||||||||||
прямой превращается в уравнение прямой |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x − x0 |
|
= |
y − y0 |
, |
|
|
|
|
|
|
(17.16) |
||||
|
|
|
|
|
|
x0 |
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
||
лежащей в плоскости кривой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
y = f (x), |
|||||||
Если эта |
кривая задается |
|
непрерывной |
функцией |
|||||||||||||||||
a x b, дифференцируемой в точке x0 (за параметр на кривой |
||||
взята переменная x), то уравнение касательной в |
точке (x0, y0), |
|||
y0 = f (x0), в силу формулы (17.16) имеет вид |
x − x0 |
= |
y − y0 |
, т. е. |
|
1 |
|
f (x0) |
|
y = f (x0)(x − x0) + y0. |
|
(17.17) |
||
Таким образом, получилось, конечно, то же самое уравнение касательной к графику функции, что и раньше (п. 10.3).
Сформулируем еще несколько определений, которые будут использоваться в дальнейшем.
Непрерывно дифференцируемая кривая без особых точек называется гладкой кривой.
Кривая Γ = {r(t) ; a t b} называется объединением кривых Γi,
если
Γi = {r(t) ; ti−1 t ti}, i = 1, 2, ..., n, a = t0 < t1 < ... < tn−1 < tn = b.
Очевидно, что в этом случае начало кривой Γ1 является и началом
кривой Γ, конец кривой Γn — концом Γ, а конец каждой кривой Γi — началом Γi+1, i = 1, 2, ..., n − 1.
