5.1.Постановка задачи.

Выберем некоторую систему функций , заданных на отрезке, и будем строитькак их линейную комбинацию:

,

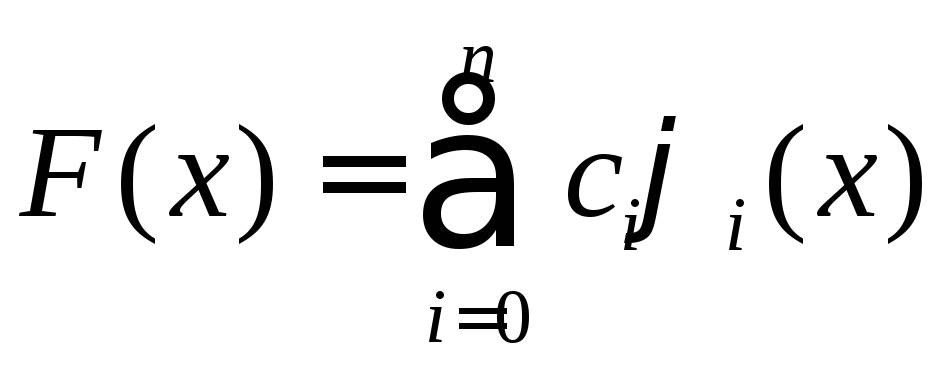где числовые коэффициенты подлежат определению, согласно условиям:

, .

Равенства представляют собой систему линейных алгебраических уравнений относительно коэффициентов :

,

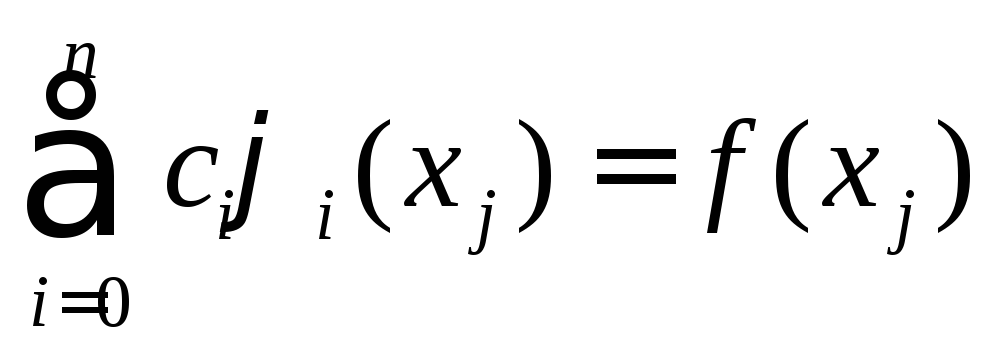или в развернутом виде:

.

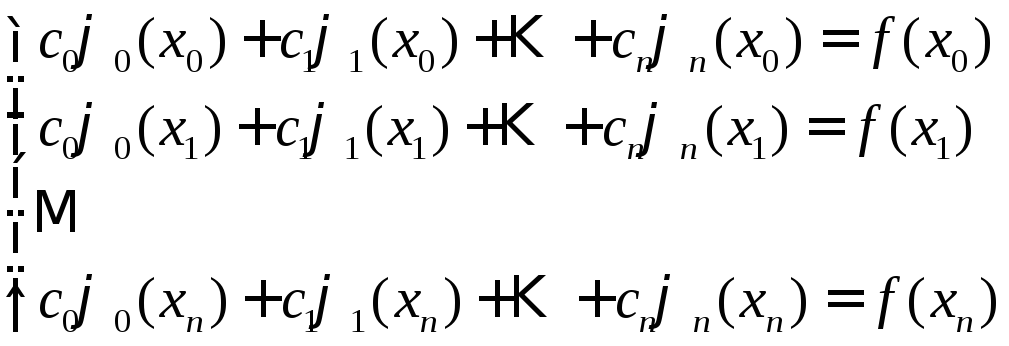Для того, чтобы коэффициенты можно было определить и притом единственным образом, необходимо и достаточно, чтобы определитель полученной системы линейных уравнений был отличен от нуля:

.

Определение.

Система функций удовлетворяющая при фиксированных значенияхусловию , называется Чебышевской.

Очевидно, что для однозначной разрешимости задачи интерполирования в классической постановке необходимо и достаточно, чтобы система функций была Чебышевской. Только такие системы функций мы и будем использовать в этой главе. Необходимым условием принадлежности системы функцийк Чебышевской является их линейная независимость.

5.2.Формула Лагранжа.

.

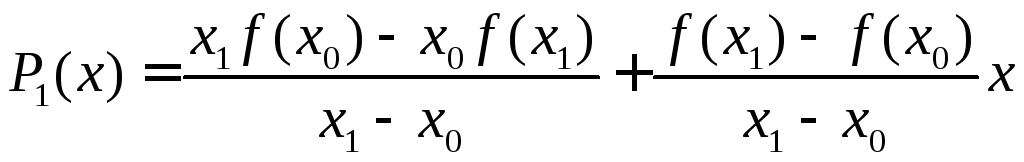Перепишем этот полином в несколько другой форме, выделяя ив качестве множителей

.

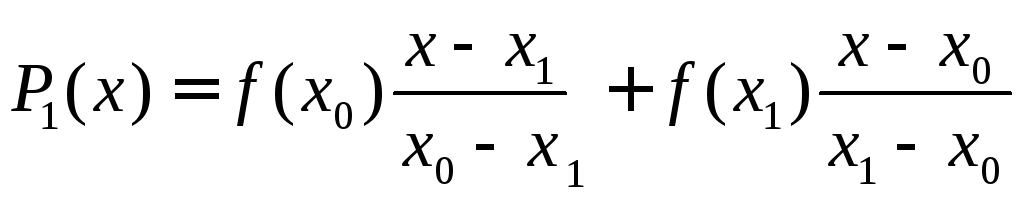Интерполяционный полином первой степени мы построили, решая напрямую систему двух уравнений с двумя неизвестными - коэффициентами и. Однако решить таким же образом систему при произвольном технически очень сложно. Проще сделать это с помощью специальных методов, учитывающих особенности рассматриваемой задачи. Один из таких методов, принадлежащих Лагранжу, мы и рассмотрим в этом разделе.

Представим искомый полином в виде:

,

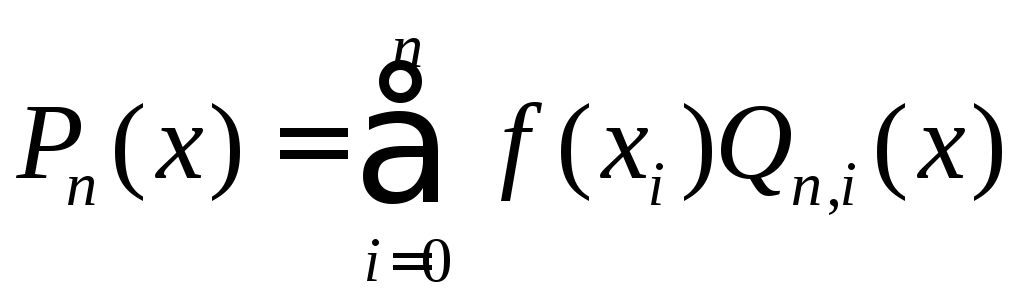где полиномы степени, «ориентированные» на точкив том смысле, что

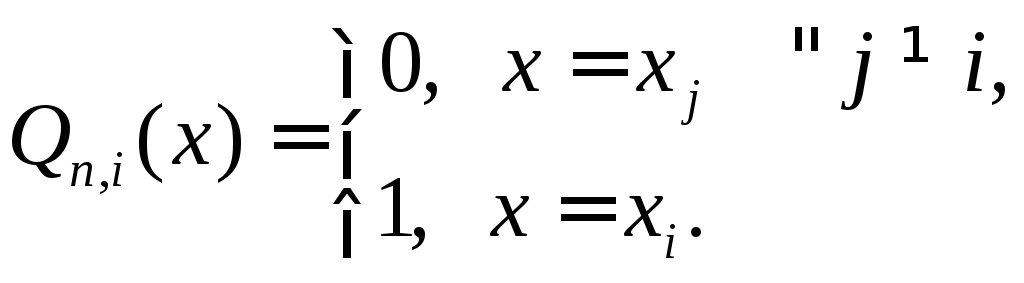
Такие полиномы легко построить:

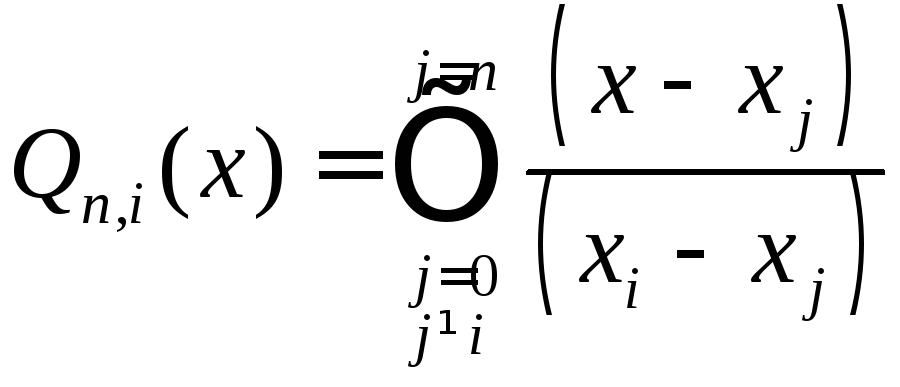
или в развернутом виде:

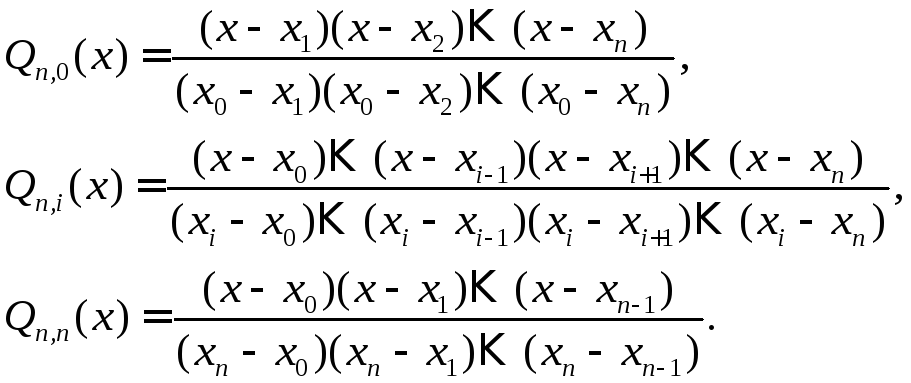
Иногда нам будет удобно записывать в виде:

.

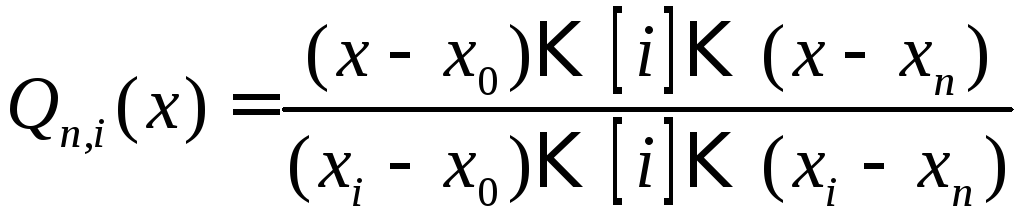Из выражения и формул очевидно, что построенный полином действительно является интерполяционным полиномом для функциина сетке с узлами. Его принято называть интерполяционным полиномом в форме Лагранжа. Этим подчеркивается, что возможны и другие эквивалентные представления интерполяционного полинома. С одним из них мы познакомимся в следующем разделе.

В заключение отметим, что из трех различных представлений интерполяционного полинома первой степени - формула дает его запись в форме Лагранжа.

5.3.Формула Ньютона.

Интерполяционный полином в форме Лагранжа, несмотря на своё изящество, неудобен для вычислений тем, что при увеличении числа узлов интерполяции приходится перестраивать весь полином заново.

Перепишем интерполяционный полином Лагранжа в иной, эквивалентной форме

,

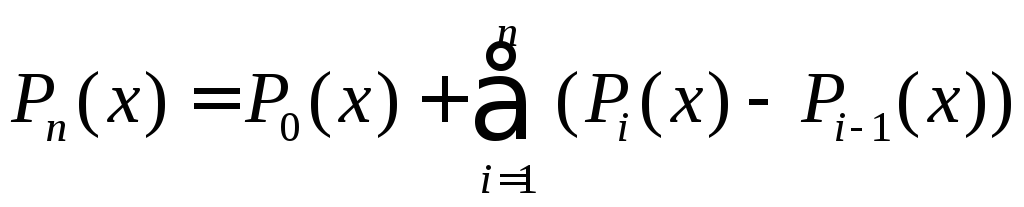где - полиномы Лагранжа степени, соответствующие узлам интерполирования. В частности,- полином нулевой степени.

Полином

имеет степень и по построению обращается в ноль припоэтому его можно представить в виде

,

где - числовой коэффициент при. Посколькуне содержит степени, топросто совпадает с коэффициентом прив полиноме.Согласно и его можно записать в виде

,

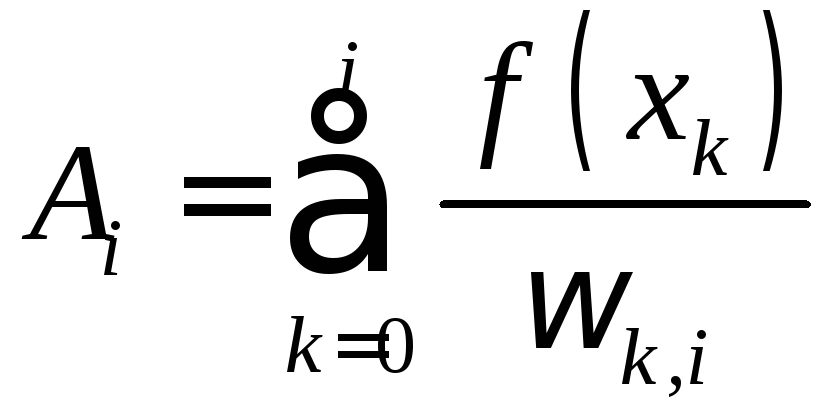где

.

При этом

.

Формулы и позволяют написать рекуррентное соотношение для полинома :

.

Выражая аналогичным образом по индукции через,черези т. д., получим окончательную формулу для полинома:

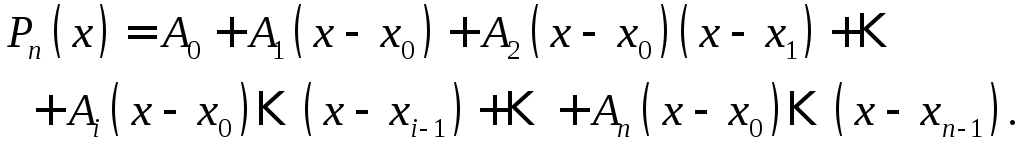
Представление удобно для вычислителя, поскольку увеличение на единицу требует только добавления к «старому» многочлену одного дополнительного слагаемого. Такое представление интерполяционного полиноманазывают интерполяционным полиномом в форме Ньютона.

Из трех эквивалентных представлений интерполяционного полинома первой степени - формула дает его запись в форме Ньютона.