9.1.Интегральное представление задачи Коши.

9.2.Метод Эйлера (метод касательных, ломанных и т. д.) Оценка погрешности.

9.3.Метод Эйлера-Коши (метод предиктор-корректор). Оценка погрешности.

9.4.Метод Рунге-Кутты 4-ого порядка точности.

На практике широко распространен Метод Рунге - Кутта четвертого порядка :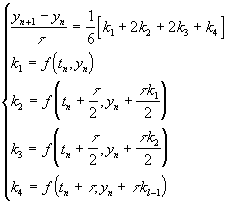

Данная схема имеет четвертый порядок аппроксимации.    

9.5.Сведение задачи Коши для уравнений n-порядка к системе ОДУ 1-ого порядка (задача Коши для системы).

9.6.Понятие краевой задачи для ОДУ 2-ого порядка.

9.7.Метод стрельбы (пристрелки).

9.8.Пример жесткой задачи Коши.

11. Методы оптимизации функций.

Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных.

В процессе решения задачи оптимизации обычно необходимо найти оптимальные значения некоторых параметров, определяющих данную задачу. При решении задач эти параметры обычно называют переменными или факторами оптимизации. Их число (x₁, x₂, … , x_n) определяет размерность задачи оптимизации.

Выбор оптимального решения или сравнение двух альтернативных решений проводится с помощью некоторой зависимой величины. Эта величина называется целевой функцией. В процессе решения задачи оптимизации должны быть найдены такие значения переменных оптимизации, при которых целевая функция имеет минимум (или максимум).

Целевую функцию в общем виде можно записать следующим образом

u = f(x₁, x₂, …, x_n)

Различают одно- и многофакторную оптимизацию. В случае однофакторной оптимизации целевая функция является функцией одной переменной, и ее график - некоторая кривая на плоскости. При n=2, например, целевая функция является функцией двух переменных, и ее графиком является поверхность.

Целевая функция не всегда может быть представлена в виде формулы. Иногда она может принимать некоторые дискретные значения, задаваться в виде таблицы и т.п.

Задачи оптимизации. Можно выделить два типа задач оптимизации - безусловные и условные.

10.1.Обусловленность задачи поиска минимума.

Будем искать минимум функции f(x), которая определена на отрезке [a,b] и унимодальна (т.е. на данном отрезке имеет только один минимум).

Процесс решения задачи методом поиска состоит в последовательном сужении интервала изменения фактора оптимизации, называемого интервалом неопределенности. В начале процесса оптимизации его длина равна b-a, а к концу она должна стать меньше заданного допустимого значения , т.е. оптимальное значение параметра оптимизации должно находиться в интервале неопределенности - отрезке [x_n, x_n+1], причем x_n+1 - x_n <  .

Наиболее простым способом сужения интервала неопределенности является деление его на некоторое число равных частей с последующим вычислением значений целевой функции в точках разбиения. Пусть n - число элементарных отрезков, h = (b-a)/n - шаг разбиения. Вычисляют значения целевой функции y_k = f_k(x) в узлах x_k = a + k h (k=0,1, … , n). Сравнивая полученные значения f(x_k), среди них находят минимальное. В данном методе, который можно назвать методом перебора, основная трудность состоит в выборе n и оценке погрешности.

Более экономичным способом уточнения оптимального параметра является использование свойства унимодальности целевой функции, которое позволяет построить процесс сужения интервала неопределенности. Если оптимальное значение функции находится в точке x_i, то из рисунка видно, что оптимальное значение функции может находиться в интервале [x_i-1, x_i+1], т.е. интервал неопределенности сужается до длины двух шагов. Если этот интервал слишком велик, то его можно снова уменьшить путем нового разбиения. Получится интервал, равный двум длинам нового шага разбиения, и т.д.

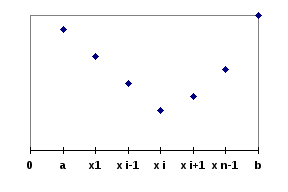
В описанном методе можно с помощью разумного выбора шага разбиения добиться эффективного поиска.

10.2.Метод дихотомии.