3) В r выполнены неравенства

или неравенства

то процесс последовательных приближений сходится к решению x = x*, y = y* .

Оценка погрешности n-го приближения определяется неравенством:

где M - наибольшее из чисел q₁ и q₂, входящих в эти неравенства.

4.2.Метод Ньютона.

В основе метода Ньютона для системы уравнений лежит использование разложения функ­ций F_i(x₁, x₂, … , x_n) в ряд Тейлора, причем члены, содержащие вторые производные (и производ­ные более высоких порядков), отбрасываются.

Пусть приближенные значения неизвестных системы (например, полученные на предыду­щей итерации) равны соответственно а₁, а₂, … , а_n .Задача состоит в нахождении приращений (по­пра­вок) в этим значениям x₁, x₂, … , x_n , благодаря которым решение исходной системы за­пи­шется в виде:

x₁ = a₁ + x₁ , x₂ = a₂ + x₂ , , . . . . . , x_n = a_{n +} x_{n .}

Проведем разложение левых частей уравнений исходной системы в ряд Тэйлора, ограничи­ва­ясь лишь линейными членами относительно приращений:

. . . . . . . . . . . . . . . . . .

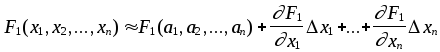
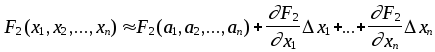
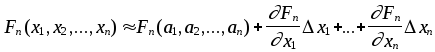
Поскольку левые части этих выражений должны обращаться в ноль, то можно приравнять ну­лю и правые части:

. . . . . . . . . . . . . . . . . .

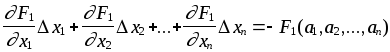
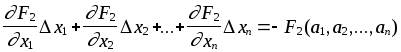
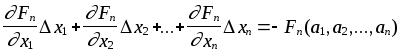
Значения F₁, F₂ , … , F_n и их производные вычисляются при x₁ = a₁ , x₂ = a₂ , … , x_n = a_n­ .

Определителем последней системы является якобиан:

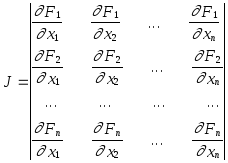
Для существования единственного решения системы якобиан должен быть отличным от нуля на каждой итерации.

Таким образом, итерационный процесс решения системы нелинейных уравнений методом Ньютона состоит в определении приращений x₁, x₂, … , x_n к значениям неизвестных на каждой итерации. Счет прекращается, если все приращения становятся малыми по абсолютной величине:

В методе Ньютона также важен удачный выбор начального приближения для обеспечения хо­рошей сходимости. Сходимость ухудшается с увеличением числа уравнений системы.

В качестве примера можно рассмотреть использование метода Ньютона для решения систе­мы двух уравнений:

F₁(x,y) = 0

F₂(x,y) = 0

где F₁ и F₂ - непрерывно дифференцируемые функции.

Пусть начальные значения неизвестных равны a, b .

После разложения исходной системы в ряд Тэейлора можно получить:

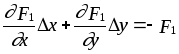
Предположим, что якобиан системы при x = a и y = b отличен от нуля:

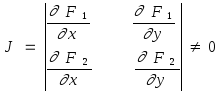
Тогда значения x и y можно найти, используя правило Крамера следующим образом:

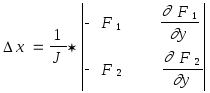и

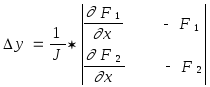
Вычислив значения x и y можно найти следующие приближения неизвестных по фор­му­лам:

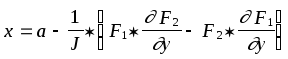
Величины, стоящие в правой части, вычисляются при x = a и y = b .

5. Интерполяция функций.

Пусть на отрезке определена некоторая функцияоднако полная информация о ней недоступна. Известны лишь ее значения в конечном числе точекэтого отрезка, которые мы будем считать занумерованными в порядке возрастания:

.

Требуется по известным значениям

,

«восстановить», хотя бы приближенно, исходную функцию то есть построить на отрезкефункцию, достаточно близкую к. Функциюпринято называть интерполирующей функцией, точки- узлами интерполяции.

Подобные задачи часто возникают на практике, например, при обработке экспериментальных данных, когда значения переменной , зависящей от, измеряется в конечном числе точек: , или при работе с табличными функциями, если требуется вычислить при значениях аргумента , не совпадающего ни с одним из табличных.

Поставленный выше в общей форме вопрос о приближении функций является достаточно сложным. Существует не один подход к его решению. Мы ограничимся изложением трех наиболее распространенных методов.