2.3.Методы уточнения корней простой итерации.

Сущность этого метода заключается в следующем. Пусть дано уравнение f(x) = 0, где f(x) - непрерывная функция, и требуется определить ее вещественные корни. Для этого заменяют исходное уравнение равносильным:

x = (x).

Выбрав приближенное значение корня x₀ подставляют его в правую часть этого уравнения. Тогда получают:

x₁ = (x₀).

После этого процесс продолжают:

x₂ = (x₁) … x_n = (x_n-1).

Если эта последовательность - сходящаяся, т.е. существует предел , то, переходя к пределу в выраженииx_n = (x_n-1) и предполагая функцию (x) непрерывной, можно найти:

или

 = ().

Таким образом, предел  является корнем уравнения и может быть вычислен по приведенной формуле с любой степенью точности.

₀

Y=x

Y=(x)

Y=x

Y=(x)

y

y

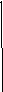
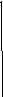
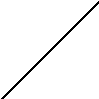
X₀

X₁

X₂

X₀

X₁

X₂

X₃

На приведенных рисунках процесс итерации сходится (кривая y = (x) в окрестности корня  - пологая, т.е.  '(x) < 1).

X₀

X₁

X₂

y

X

Y=x

(x)=f(x)+x,где :

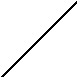
если f '(x)>0, то –1/r<<0; если f '(x)<0, то –1/r>>0, где r=max(| f '(a)|, |f '(b)|).

Однако, если рассмотреть случай, где '(x) > 1, то процесс итерации может быть рас­ходящимся.

Поэтому для практического применения ме­тода итерации нужно выяснить достаточные условия сходимости итерационного процесса.

(см. вопрос№2.6.)

2.4.Метод Ньютона.

Пусть корень  уравнения f(x) = 0 отделен на отрезке [a,b], причем f '(x) и f "(x) непрерывны и сохраняют определенные знаки при a  x  b. Найдя какое-нибудь n-е приближение корня x_n   (a  x_n  b), можно уточнить его по методу Ньютона следующим образом. Положим  = x_n + h_n , где h_n считают малой величиной. Отсюда, применяя формулу Тейлора, получим

0 = f(x_n + h_n)  f(x_n) + h_n f '(x_n) .

Следовательно,

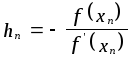
Отсюда можно найти следующее (по порядку) приближение корня:

X₀

X₁

y

F(x₀)

B

B=x₀

a

0



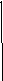
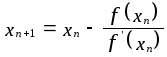, (n = 0, 1, 2, …)

Как видно из этого рисунка правильный выбор начального приближения обеспечивает удачу в по­иске корня. Общее правило - "хорошим" начальным приближением является то, для которого выполня­ется неравенство:

f(x₀) f "(x₀) > 0 .

Из общей формулы метода вытекает, что чем больше численное значение первой производной в окрестности данного корня, тем меньше поправка, которую нужно прибавить к n-му приближению, чтобы получить n+1 приближение. Поэтому метод Ньютона удобно применять тогда, когда в окрестности данного корня график функции имеет большую крутизну. Но если численное значение первой производной близ корня мало, то поправки будут велики, и вычисление корня по этому методу может оказаться очень долгим, а иногда и вовсе невозможным.

2.5.Метод хорд.

Пусть для определенности f(a) < 0 и f(b) > 0. Тогда, вместо того, чтобы делить отрезок [a,b] пополам, более естественно разделить его в соотношении f(a)/f(b) . Это дает приближенное значение корня x₁ = a + h .

Для вычисления значения h можно составить пропорцию (см.рисунок)

Откуда

b

B

f(b)

a

A

x



x

y

0

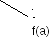
Далее, применяя этот прием к тому из отрезков [a,x] или [b,x], на концах которого функция f(x) имеет противоположные знаки, получим второе приближение корня и т.д.

Геометрически способ пропорциональ­ных частей эквивалентен замене кривой y = f(x) хордой, проходящей через точки A [a, f(a)] и B [b, f(b)]. Отсюда можно получить еще одну формулу этого метода. Из подобия треугольников вытекает, что

. Отсюда .