3.1.3.Обусловленность слау

Таким образом, малые погрешности вычислений или исходных данных могут привести к существенным погрешностям в решении. Такие системы уравнений называются плохо обусловленными.

Для оценки полученного решения используют следующее соотношение:

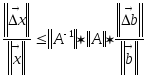
Произведение называется числом обусловленности матрицы A и обозначается как cond(A).

3.1.Метод Гаусса.

Он основан на приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы.

Сначала с помощью первого уравнения исключается х₁ из всех последующих уравнений системы. Затем с помощью второго уравнения исключается х₂ из третьего и всех последующих уравнений. Этот процесс, называемый прямым ходом метода Гаусса, продолжается до тех пор, пока в левой части последнего (n-го) уравнения не останется лишь один член с неизвестным x_n, т.е. матрица системы будет приведена к треугольному виду.

Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных: решая последнее уравнение находят единственное неизвестное x_n. Далее, используя это значение, из предыдущего уравнения вычисляют x_n-1 и т.д. Последним находят значение х₁ из первого уравнения.

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ = b₁

a₂₁x₁ + a₂₂x₂ + a₂₃x₃ = b₂

a₃₁x₁ + a₃₂x₂ + a₃₃x₃ = b₃

Для исключения х₁ из второго уравнения прибавим к нему первое, умноженное на -а₂₁/а_{11 .}

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ = b₁

(a₂₂-а₂₁/а₁₁)x₂ + (a₂₃-а₂₁/а₁₁)x₃ = b₂-(а₂₁/а₁₁)b₁

a₃₁x₁ + a₃₂x₂ + a₃₃x₃ = b₃

Затем, умножив первое уравнение на -а₃₁/а₁₁ и прибавив результат к третьему уравнению, исключим из него х₁

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ = b₁

(a₂₂-а₂₁/а₁₁)x₂ + (a₂₃-а₂₁/а₁₁)x₃ = b₂-(а₂₁/а₁₁)b₁

(a₃₂-а₃₁/а₁₁)x₂ + (a₃₃-а₃₁/а₁₁)x₃ = b₃-(а₃₁/а₁₁)b₁

Общие формулы пересчета коэффициентов при этом выглядят следующим образом:

a'_ij = a_ij - (a_i1/a₁₁)a_1j (i,j = 2,3)

b'_i = b_i - (a_i1/a₁₁)b₁ (i = 2,3)

Т.е. система имеет вид

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ = b₁

a'₂₂x₂ + a'₂₃х₃ = b'₂

a'₃₂x₂ + a'₃₃x₃ = b'₃

Теперь из третьего уравнения системы надо исключить х₂. Для этого надо умножить второе уравнение на -a'₃₂/a'₂₂ и прибавить результат к третьему. В результате получится

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ = b₁

a'₂₂x₂ + a'₂₃х₃ = b'₂

a''₃₃х₃ = b''₃

где a''₃₃ = a'₃₃ - (a'₃₂/a'₂₂)a'₂₃ и b''₃ = b'₃ - (a'₃₂/a'₂₂)b'₂ .

Матрица полученной системы имеет треугольный вид.

В процессе исключения неизвестных приходится выполнять операции деления на коэффициенты а₁₁, а₂₂ и т.д. Поэтому они должны быть отличными от нуля. В противном случае необходимо соответствующим образом переставить уравнения системы. Диагональные элементы матрицы обычно называют ведущими или главными элементами.

Обратный ход начинается с решения третьего уравнения системы

x₃ = b''₃/a''₃₃ .

Используя это значение, можно найти х₂ из второго уравнения, а затем х₁ из первого:

x₂ = (b'₂ - a'₂₃x₃)/a'₂₂ ; x₁ = (b₁ - a₁₂x₂ - a₁₃x₃)/a₁₁

Аналогично строится вычислительный алгоритм для линейной системы с произвольным числом уравнений. При этом расчетные формулы принимают вид:

Прямой ход метода Гаусса

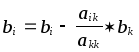, , где

k=1,2,…,n-1 ; i=k+1,k+2,…,n ; j=k+1,k+2,…,n .

В этих формулах k - номер неизвестного, которое исключается из оставшихся n-k уравнений (а также номер того уравнения, с помощью которого исключается x_k); i - номер уравнения, из которого исключается неизвестное x_k; j - номер столбца.

Обратный ход метода Гаусса

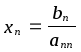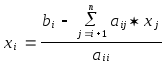; , где i=n-1,n-2,…,1 .

В этих формулах i - номер неизвестного, которое определяется из i-го уравнения; j=i+1,i+2,… - номера уже найденных неизвестных.