1. Элементы теории погрешностей.

1.1.Определение абсолютной и относительной погрешности численного результата.

Приближенным числом а называется число, незначительно отличающееся от точного А и заменяющее последнее в вычислениях. Под ошибкой или погрешностью а приближенного числа а обычно понимается разность между соответствующим точным числом А и данным приближением, т.е.

а = А - а .

Абсолютной погрешностью  приближенного числа а называется абсолютная величина разности между соответствующим точным числом А и числом а, т.е.

 = А - а .

Если число А не известно, то по этой формуле нельзя определить абсолютную погрешность, Поэтому вместо неизвестной теоретической абсолютной погрешности вводят ее оценку сверху, называемую предельной абсолютной погрешностью .

Под предельной абсолютной погрешностью приближенного числа понимается всякое число, не меньшее абсолютной погрешности этого числа. Таким образом, если а - предельная абсолютная погрешность, то

 = А - а  а .

Относительной погрешностью  приближенного числа а называется отношение абсолютной погрешности  этого числа к модулю соответствующего точного числа А (А0) т.е.

.

Так же как и для абсолютной погрешности вводят понятие предельной относительной погрешности. Под предельной относительной погрешностью _а понимают всякое число, не меньшее относительной погрешности этого числа. В качестве предельной относительной погрешности числа а можно принять число

.

1.2.Основные составляющие абсолютной погрешности.

1.3.Формулы для оценки абсолютной и относительной погрешности для значения функции и переменных.

При сложении или вычитании чисел их абсолютные погрешности складываются. Относительная погрешность суммы заключена между наибольшим и наименьшим значениями относительных погрешностей слагаемых; на практике принимается наибольшее значение.

(a  b) = a + b .

При умножении или делении чисел друг на друга их относительные погрешности складываются.

;

При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени.

Погрешность разности: предельная абсолютная погрешность разности (u = x₁ - x₂) равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого:

_u = _x1 + _x2

Отсюда предельная относительная погрешность разности

где А - точное значение абсолютной величины разности чисел х₁ и х₂ .

Погрешность произведения: относительная погрешность произведения нескольких приближенных чисел, отличных от нуля, не превышает суммы относительных погрешностей этих чисел:

  ₁ + ₂ + ... + _{n .}

Поэтому при вычислении произведения нескольких приближенных чисел применяют следующие правила:

- округляют эти числа так, чтобы каждое из них содержало на одну (или две) значащие цифры больше, чем число верных значащих цифр в наименее точном из сомножителей;

- в результате умножения сохраняют столько значащих цифр, сколько верных цифр имеется в наименее точном из сомножителей.

Погрешность частного: относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя.

Основная задача теории погрешности заключается в следующем: известны погрешности некоторой системы величин, требуется определить погрешность данной функции от этих величин.

Пусть задана дифференцируемая функция u=(x₁,x₂, ... , x_n) и пусть x_i - абсолютные погрешности аргументов функции.

Тогда предельная абсолютная погрешность функции может быть вычислена по формуле:

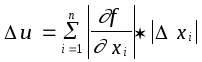
Предельная относительная погрешность функции вычисляется следующим образом: