5.4.Оценка погрешности интерполяции.

Поставим вопрос о том, насколько хорошо интерполяционный полином приближает функциюна отрезке, то есть попытаемся оценить погрешность (остаточный член)

,.

Сразу же отметим, что по определению интерполяционного полинома

при,

поэтому речь идет об оценке при значениях.

Для того, чтобы это сделать, следует ввести дополнительно предположение о гладкости функции . Предположим, чтоимеетнепрерывную производную на отрезке.

В силу можно представить в виде:

,

где - полином степени:

.

Зафиксируем произвольное значение и рассмотрим вспомогательную функцию от переменной:

,

заданную на отрезке и содержащую переменнуюв качестве параметра. В силу своего определения функцияобязана обращаться в нуль в узлах интерполирования прии кроме того при , т. е. как функция аргументаона имеетнуля:

,,.

Если , то все ее нули также лежат на отрезке. Еслито эти нули, вообще говоря, принадлежат отрезку, а если, то они находятся на отрезке. Объединяя эти три случая, скажем, что указанные нули функциипринадлежат отрезку, где.

Согласно известной теореме Ролля можно утверждать, что производная имеет по крайней меренуль на отрезке(эти нули перемежаются с нулями самой функции). Повторяя это рассуждение, заключаем, чтоимеет по крайней меренулей на отрезке,-нуль и, наконец,обращается хотя бы один раз в нуль в некоторой точке, то есть

.

Учитывая, что производная полинома степенитождественно равна нулю, получаем, что

;

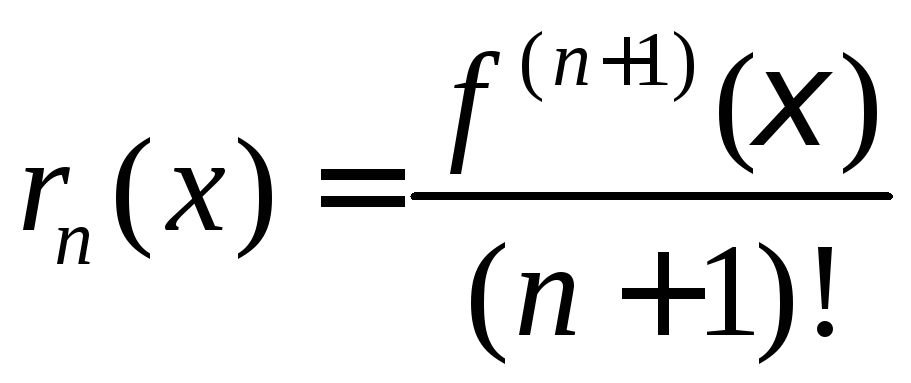и соответственно

.

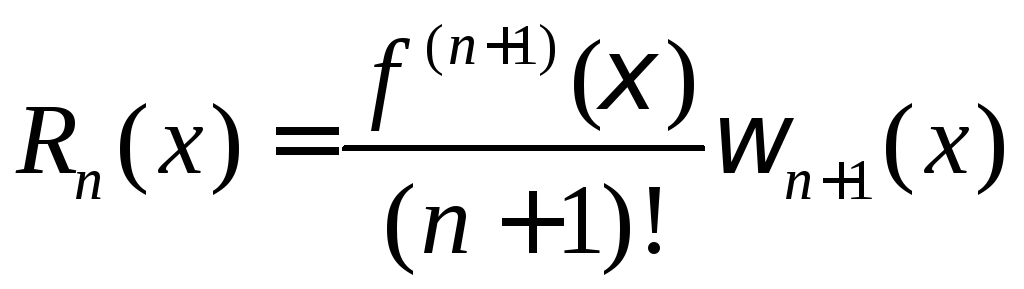Формула не позволяет вычислить погрешность, поскольку точное значение аргумента нам неизвестно. Однако с ее помощью погрешность можно оценить:

,

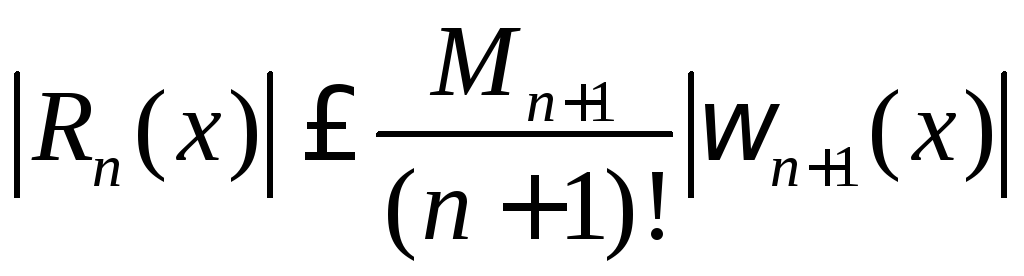где

.

Обсудим роль полинома в оценке . На отрезкеон имеетнуль, а его значения между этими нулями сравнительно невелики, но, когда точкавыходит за пределы отрезкаи удаляется от точкивлево или от точкивправо, оценка ухудшается из-за быстрого роста функции. Это хорошо видно на рис. 2, где в качестве примера приведен график функциис корнями,,,:

.

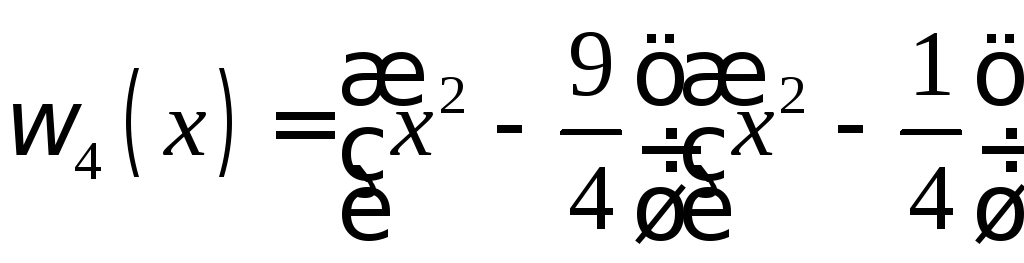Ее наибольшее по модулю значение на отрезке 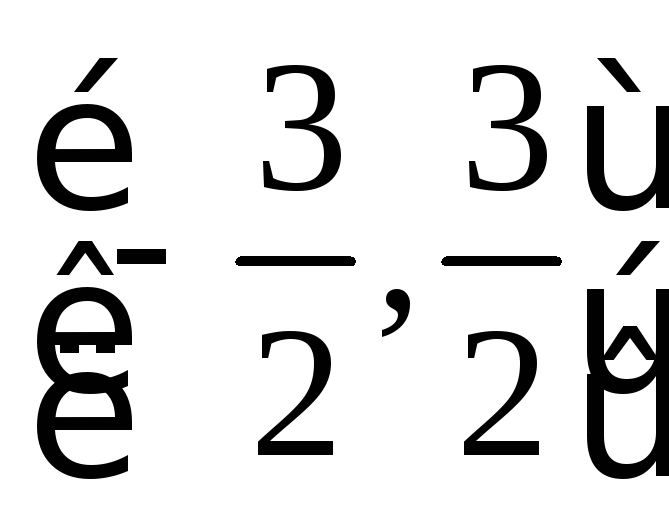равно единице. Однако уже в точкахза пределами отрезка полиномпринимает значение

.

Из сказанного можно сделать следующий вывод. Если , то множительне обесценивает оценку . Такой случай называют собственно интерполяцией. Противоположный случай, когда точкалежит вне отрезка называют экстраполяцией функции. Отмеченная выше особенность поведения полиномарезко ухудшает оценку при экстраполяции. Поэтому на практике экстраполяции избегают или ограничиваются многочленами невысокой степени, когда рост функциине настолько критичен.

5.5.Интерполяция сплайнами.

Увеличение степени интерполяционного полинома может оказаться невыгодным из-за быстрого роста объема вычислений. К тому же далеко не всегда оно приводит к повышению точности. Во второй половине ХХ века с появлением компьютеров и развитием современной вычислительной математики при обработке больших таблиц получила развитие новая идея – строить приближение функций с помощью кусочно-полиномиальной интерполяции с использованием полиномов сравнительно невысоких степеней. Наиболее удобными оказались полиномы третьей степени. Такие конструкции получили название кубических сплайнов.