
- •1. Статистическая обработка результатов эксперимента Физические измерения
- •Погрешности физических измерений
- •Оценка величины систематической погрешности
- •Оценка погрешности при прямых однократных измерениях
- •Оценка величины случайной погрешности
- •Оценка погрешности при прямых многократных измерениях
- •Оценка погрешности косвенных измерений
- •1.1. Определение погрешности прямого многократного
- •1.2. Определение погрешности косвенного измерения удельного сопротивления. (Лабораторная работа 2) Теория метода и описание прибора
- •Порядок выполнения работы и обработка результатов измерений
- •Вычисление погрешности измерения удельного сопротивления
- •Контрольные вопросы
- •2. Кинематика и динамика поступательного движения тел
- •2.1. Измерение ускорения свободного падения на машине Атвуда. (Лабораторная работа 3)
- •Теория метода и описание прибора
- •Порядок выполнения работы и обработка результатов измерений
- •Подготовка прибора к измерениям
- •Измерения
- •Контрольные вопросы
- •2.2. Проверка второго закона Ньютона с помощью машины Атвуда. (Лабораторная работа 4)
- •Теория метода и описание прибора
- •Порядок выполнения работы и обработка результатов измерений Задание 1. Проверка закона пути .
- •Обработка результатов измерений
- •Контрольные вопросы
- •2.3. Исследование прямолинейного движения тел в поле силы тяжести. (Лабораторная работа 5)
- •Теория метода и описание прибора
- •Порядок выполнения работы и обработка результатов измерений Подготовка прибора к измерениям
- •3. Кинематика и динамика вращательного движения твердого тела
- •3.1. Изучение законов вращательного движения на маятнике Обербека. (Лабораторная работа 6)
- •Теория метода и описание прибора
- •Порядок выполнения работы и обработка результатов измерений
- •Подготовка прибора к измерениям
- •Измерения
- •Контрольные вопросы
- •4. Закон сохранения импульса и закон сохранения механической энергии
- •Удар – совокупность явлений, связанных со значительными изменениями скорости тела за малый промежуток времени (тысячные доли секунды).
- •В качестве меры механического взаимодействия тел при ударе служит импульс силы за время удара:
- •4.1. Проверка закона сохранения механической энергии с помощью прибора Гримзеля. (Лабораторная работа 7)
- •Теория метода и описание прибора
- •Порядок выполнения работы и обработка результатов измерений
- •Контрольные вопросы
- •4.2. Удар шаров. (Лабораторная работа 8)
- •Теория метода и описание прибора
- •Порядок выполнения работы и обработка результатов измерений
- •Контрольные вопросы
- •4.3. Определение момента инерции и проверка закона сохранения энергии с помощью маятника Максвелла. (Лабораторная работа 9)
- •Теория метода и описание прибора
- •Описание прибора
- •Порядок выполнения работы и обработка результатов измерений
- •Контрольные вопросы
- •5. Закон изменения момента импульса и закон сохранения момента импульса
- •Порядок выполнения работы и обработка результатов измерений
- •Контрольные вопросы
- •5.2. Изучение прецессии гироскопа. (Лабораторная работа 11)
- •Теория метода и описание прибора
- •Порядок выполнения работы и обработка результатов измерений
- •Контрольные вопросы
- •6. Механические колебания. Физический маятник
- •6.1. Определение ускорения свободного падения с помощью оборотного маятника. (Лабораторная работа 12)
- •Теория метода и описание прибора
- •Порядок выполнения работы и обработка результатов измерений
- •Контрольные вопросы
- •6.2. Определение ускорения свободного падения с помощьюмаятника универсального. (Лабораторная работа 13)
- •Теория метода и описание прибора
- •Порядок выполнения работы и обработка результатов измерений
- •Контрольные вопросы
Оценка величины случайной погрешности
Случайные погрешности являются следствием случайных, неконтролируемых помех, влияние которых на процесс измерения невозможно учесть непосредственно, проявляются в хаотическом изменении результатов повторных наблюдений, могут отклонять результаты измерения от истинного значения в обе стороны. При обработке результатов эксперимента возникают два вопроса: 1) как найти из полученных значений наиболее вероятное значение измеряемой величины и 2) чему равна ожидаемая погрешность измерений? Ответ на эти вопросы дается теорией вероятностей. Согласно этой теории, случайные погрешности измерений подчиняются закону нормального распределения Гаусса.
Смысл закона Гаусса заключается в следующем. Допустим, мы хотим измерить некоторую физическую величину, истинное (и нам неизвестное) значение которой есть хо. Проведя несколько раз измерения, вместо хо получаем набор значений х1, х2,… хi,… xn. Оказывается, что с помощью закона распределения мы хотя и не можем указать точное значение хо, но можем найти, с какой вероятностью Р величина хо окажется в любом интервале значений а<xo<b. Область значений а<xo<b называют доверительным интервалом. По закону Гаусса эта вероятность определяется функцией плотности распределения
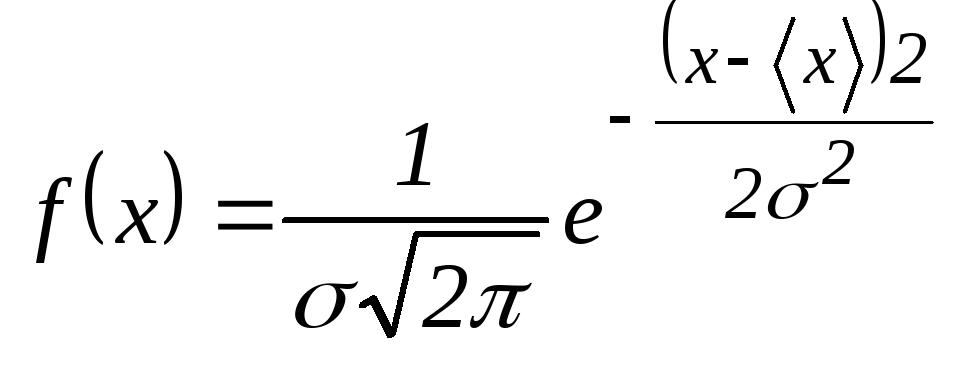 (1.4)
(1.4)
и равна
![]() . (1.5)
. (1.5)
Функция
плотности распределения f(x)
характеризует число случаев, когда
измеряемая величина попала в интервал
от x
до
x+dx
(dx
– малое изменение измеряемой величины).
x
–
набор значений, которые мы получаем в
результате измерения, x
– их среднее арифметическое, а
![]() среднее
квадратичное отклонение
среднее
квадратичное отклонение
![]() , (1.6)
, (1.6)
 . (1.7)
. (1.7)

Рис. 1.1
Как видно из рис.1.1, гауссова кривая, имеющая на графике симметричный колоколообразный вид, характеризуется двумя параметрами: положением вершины x и шириной 2σ – расстоянием между точками перегиба. Значение x обычно принимают за ту величину, которую надо было измерить, а σ характеризует степень влияния случайных погрешностей на результаты измерения: чем меньше σ, тем уже гауссова кривая и тем, следовательно, точнее проведено измерение. Площадь под кривой от а до b определяет долю случаев, в которых измеряемая величина лежит в этом интервале (т.е. вероятность того, что измеряемая величина попала в интервал от а до b).
Следует подчеркнуть, что x – не истинное значение измеряемой величины, а лишь некоторое приближение к нему. Чем более широким выбирается доверительный интервал, тем выше вероятность попадания истинного значения в этот интервал. Так, например, вероятность отклонения истинного значения от положения вершины гауссовой кривой x не более чем на σ равна 0,683, а не более чем на 2σ – 0,955.
Бесконечное увеличение числа измерений не дает заметного увеличения точности. Зависимость надежности (вероятности) от числа измерений сложна и не выражается в элементарных функциях. Существуют специальные таблицы коэффициентов Стьюдента, по которым можно определить, во сколько раз надо увеличить стандартный доверительный интервал Sx, чтобы при определенном числе измерений n получить требуемую вероятность (надежность) Р.
Стандартный
доверительный интервал, или
среднеквадратичная погрешность среднего,
согласно выводам математической
статистики убывает пропорционально
![]() и определяется формулой
и определяется формулой
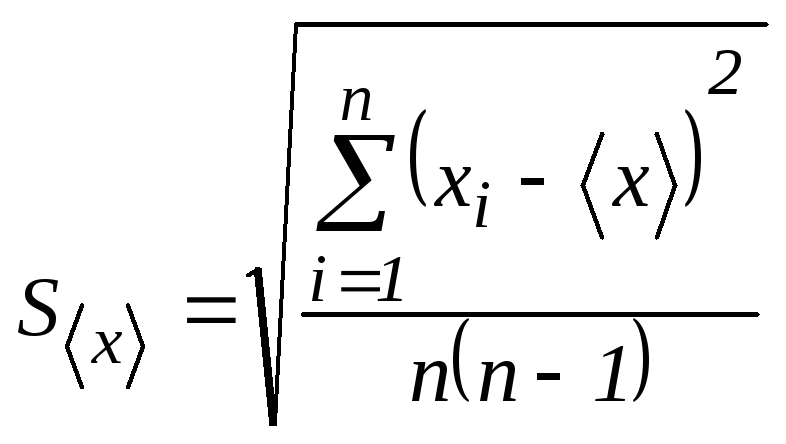 . (1.8)
. (1.8)
Таблица 1.1
Таблица коэффициентов Стьюдента t (P,n)
|
N |
P | ||||
|
0,5 |
0,7 |
0,9 |
0,95 |
0,999 | |
|
3 |
0,82 |
1,3 |
2,9 |
4,3 |
31,6 |
|
5 |
0,74 |
1,2 |
2,1 |
2,8 |
8,6 |
|
7 |
0,72 |
1,1 |
1,9 |
2,4 |
6,0 |
|
10 |
0,70 |
1,1 |
1,8 |
2,3 |
4,8 |
|
20 |
0,69 |
1,1 |
1,7 |
2,1 |
3,9 |
|
|
0,67 |
1,0 |
1,6 |
2,0 |
3,3 |
Чтобы найти величину случайной погрешности, необходимо стандартный доверительный интервал умножить на коэффициент Стьюдента:
Δхсл.= t (P,n) . Sx. (1.9)
