Н. С. Токов нулевой последовательности

необходимо рассмотреть отдельно.

Используем для н. с. фаз от токов нулевой последовательности выражение (22-21). Тогда для v-x гармоник трех фаз имеем

Рис 22-9 Образование эллиптического вращающегося поля

Очевидно, что эти н. с. во времени совпадают по фазе и сдвинуты в пространстве на

углы vj. Для гармоник, кратных трем (v =3 k), угол сдвига

составляет 2nk или 0°, и поэтому эти гармоники складываются арифметически. Но для гармоник v = 6k± 1 угол сдвига равен

Н. с. двухфазной обмотки при симметричной нагрузке токами

/ cos со^;                                                                                                                                                             )

. ._                                                                                                                                                                                                                                                                                                                                     (22-39)

сдвинутыми по фазе на 90°, можно проанализировать так же, как и для трехфазной обмотки, учитывая при этом, что фазы двухфазной обмотки сдвинуты в пространстве тоже на 90°.

Рис. 22-10. Образование вращающегося поля двухфазной обмотки

Из такого анализа получаются следующие выводы:

1.  В кривой н. с. сохраняются все нечетные гармоники, из которых гармоники

v = 2mk+l=4k+l (k = 0, 1, 2, 3 ...)          (22-40)

или v = 1, 5, 9, 13... являются прямыми, а гармоники

v = 2tnk- 1=4£-1 (k=\, 2, 3...)              (22-41)

или v = 3, 7, 11... — обратными.

2.  Амплитуда н. с. выражается равенством (22-31) при т = 2 или равенством (22-19).

Таким образом, амплитуда вращающейся н. с. двухфазной обмотки равна амплитуде пульсирующей н. с. одной фазы обмотки. Этот результат отражает то обстоятельство, что два вектора F_a и F_b, неподвижных в пространстве со сдвигом на 90° и пульсирующих

во времени со сдвигом по фазе также на 90°, в сумме образуют вращающийся вектор с той же амплитудой (рис. 22-10).

Следовательно, две- обмотки, сдвинутые в пространстве на 90°, при питании их одинаковыми по величине токами, сдвинутыми по фазе также на 90°, создают вращающееся магнитное поле.

Н. с. трехфазной обмотки при несинусоидальных токах. В некоторых случаях (работа генераторов на выпрямительную нагрузку, питание двигателей через вентильные преобразователи частоты) токи фаз несинусоидальны. В таких случаях кривую тока можно разложить на основную и высшие временные гармоники и исследовать действие каждой гармоники тока по отдельности. Каждая k-я гармоника тока, имеющая частоту /_к = kf_lt создает такой ряд пространственных гармоник н. с, как и основная гармоника, но Ъра-щающихся в k раз быстрее. Наибольшей среди них является основная пространственная гармоника с числом полюсов 2р. Магнитное поле этой гармоники вращается относительно ротора и индуктирует в массивных частях ротора синхронных машин, в их успокоительных и пусковых обмотках и в обмотках роторов асинхронных машин токи, которые вызывают излишние потери и нагрев машины.

Н. с. беличьей клетки. Анализ этого вопроса здесь опускается. Приведем лишь его результаты.

Если вращающееся магнитное поле с р парами полюсов индуктирует в беличьей клетке с Z стержнями систему токов со сдвигом по фазе в соседних стержнях на угол у [см. выражение (21-14)], то эта беличья клетка создает бесконечный ряд прямо вращающихся гармоник с порядковыми числами

Равенство (22-42) при k = 0 определяет основную- гармонику н. с. Например, при Z = 18 и р = 2 получим прямые гармоники v = 1, 10, 19, 28... и обратные гармоники v = 8, 17, 26...

Равенства (22-42) и (22-43) можно истолковать следующим образом.

В двух последних равенствах (22-29) и в равенствах (22-40), (22-41) числа б и 4 перед k равны числам фазных зон рассматриваемых обмоток на пару полюсов. В (22-42) и (22-43) величина Zip определяет количество стержней на пару полюсов. Токи в этих

стержнях сдвинуты по фазе подобно токам фазных зон обычной многофазной обмотки, и поэтому данные стержни аналогичны фазным зонам. В связи с этим вместо 2т в равенства (22-42) и (22-43) входит Zip.

При достаточно большом Zip беличья клетка имеет большое число фаз и ее н. с. содержит мало гармоник низких порядков, приближаясь поэтому к синусоиде.

Совпадение выражений (22-42), (22-43) с (22-34) указывает на то, что все гармоники н. с. беличьей клетки являются гармониками зубцового порядка. Это вполне естественно, так как в беличьей клетке каждый стержень представляет собой отдельную фазу и поэтому q = 1.

Если Zip — не целое число, то н. с. беличьей клетки содержит гармоники v дробного порядка, для которых величины полюсных делений % и t_v не являются кратными.

Амплитуды гармоник н. с. беличьей клетки определяют по равенству (22-31) при подстановке пг = Z, w — ¹/₂, k_o6v = 1. понимая под / ток стержня. Для этой н. с. действительно также выражение (22-32), если начало координат а совпадает с серединой зубца и фаза тока участка кольца у этого зубца определяется выражением /_к cos cat. Для получения надлежащих знаков членов (22-32) при этом необходимо положить

где верхний знак относится к прямым гармоникам, а нижний — к обратным и значения k для разных v соответствуют (22-42) и (22-43). Представление вращающегося поля в виде двух пульсирующих полей. Выражение для вращающейся основной гармоники н. с. [см. формулу (22-32)] можно видоизменить следующим образом:

Два члена правой части (22-45) представляют собой два неподвижных пульсирующих поля, которые сдвинуты в пространстве на 90° (cos a и sin а) и пульсируют во времени со сдвигом по фазе также на 90° (cos at и sin u>t).

Такая замена вращающегося поля двумя неподвижными пульсирующими полями удобна при анализе некоторых вопросов теории машин с электрической и магнитной несимметрией по двум взаимно перпендикулярным осям (например, явнополюс-ные синхронные машины) и может быть распространена также на высшие гармоники поля. В любом случае можно представить себе также, что такие поля создаются некоторой воображаемой двухфазной обмоткой (см. рис. 22-10).

§ 22-3. Графический метод анализа намагничивающей силы обмотки

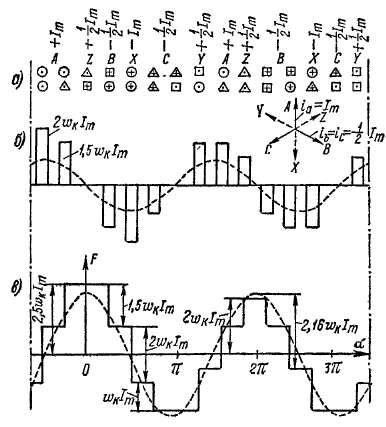
Построение кривой н. с. обмотки с целым q. Из рассмотрения рис. 22-1 следует, что кривая н. с. катушки изменяется скачком на величину полного тока катушки wJ_K в местах расположения катушечных сторон, а на участках, лишенных тока, величина н. с. не изменяется. Направление скачка кривой н. с. при этом определяется направлением тока в катушке. Поскольку для н. с применим принцип наложения, то отсюда вытекает следующий простой метод построения кривой н. с. обмотки: для определенного момента времени вычерчивается (рис. 22-11, в и е) ступенчатая кривая н. с, которая изменяется скачками соответствующей величины и направления в местах расположения катушечных сторон обмотки. Этот метод, таким образом, представляет собой в сущности графическое интегрирование токов катушечных сторон обмотки вдоль поверхности якоря.

На практике кривая н. с. строится следующим образом.

Вычерчивается график распределения катушечных сторон по фазным зонам (см. рис. 22-11, а, где сечения катушек разных фаз изображены разными фигурами). Затем для определенного момента времени определяются величины и направления токов в катушечных сторонах, которые указываются там же. На рис. 22-11, а принят момент времени, когда токи катушек в зонах А, В, С равны соответственно

а в зонах X, Y, Z они равны этим величинам с обратным знаком. Положительные токи на рис. 22-11, а обозначены точками, а отрицательные— крестиками. На рис. 22-11,6 представлен также график распределения тока пазов вдоль окружности якоря и его основная гармоника, вычерчивание которого не обязательно. При¹ вычерчивании кривой н. с. (рис. 22-11, е) откладывают в соответствующих направлениях ступеньки, равные величинам полных токов соответствующих пазов. Если ток wj_m принять за единицу,, то величина первых трех ступенек кривой рис. 22-11, в будет равна соответственно 2, 1^х/₂ и 1 единицам. Полученную кривую н. с. (рис. 22-11, в) разделяют осью абсцисс таким образом, чтобы сумма площадей положительных полуволн (полюсов) равнялась сумме площадей отрицательных полуволн (полюсов), ибо вследствие не* прерывности магнитных линий суммы потоков противоположный полярностей должны быть равны. При целом q все полуволны кри< вой имеют одинаковую форму и ось абсцисс является осью симмет* рии кривой.

На рис. 22-11, г, д и е указанные построения повторены для случая, когда фаза токов изменилась на 30° и

Кривые н. с. позволяют определить величины н. с. в любых точках окружности и, в частности, ее максимальные величины. Кривую н. с. можно разложить известными методами на гармоники (штриховые кривые на рис. 22-11, в и е для v = 1) и определить их амплитуды.

На основании рис. 22-11 можно отметить следующее.

При изменении фазы тока на некоторый угол (на рис. 22-11, е на 30° по сравнению с рис. 22-11, в) кривая н. с. в целом и ее основная гармоника смещаются на такой же угол. Изменение при этом формы кривой свидетельствует о том, что ее разные гармоники вращаются с разными скоростями. При увеличении q зубцы кривой н. с. становятся относительно меньше и удельный вес высших гармоник в кривой уменьшается. При q ->■ оо (равномерно распределенная обмотка) кривая н. с. в наибольшей степени приближается к синусоиде. Укорочение шага также приближает кривую к синусоиде, так как градация величин ступеней кривой н. с. вследствие перекрытия фазных зон разных слоев обмотки при этом увеличивается. Наилучшая кривая н. с. получается при укорочении шага обмотки на половину фазной зоны (при зоне 60° шаг у = ⁵/_вт, как на рис. 22-11), когда кривая н. с. каждого полюса состоит из 2т участков с разными крутизнами подъема вместо т участков при у = т.

Кривая н. с. дробной обмотки. На рис. 22-12 изложенным выше графическим методом построена кривая н. с. трехфазных двухслойных дробных обмоток, изображенных на рис. 21-5 и 21-7, для момента времени, когда i_a = l_m,ib — ic —

= —2^^т' '~^>ИС' 22-12 выполнен для половины окружности статора (4т). Из этого

рисунка можно сделать следующие выводы о свойствах н. с. дробных обмоток.

Формы кривых н. с. северных и южных полюсов дробной обмотки неодинаковы, и поэтому наряду с нечетными существуют также четные гармоники н. с. В общем случае, при знаменателе дробности d > 2, кривые н. с. на протяжении различных пар полюсов различны, период кривой L поэтому больше 2т (на рис. 22-12 имеем L = 4т) и при разложении ее в ряд Фурье появляются гармоники у с полюсным делением t_v > т. Порядок этих гармоник н. с. v = t/t_v < 1, и они называются низшими. Поля этих гармоник вращаются быстрее поля основной гармоники [см. равенство (22-23)]. Появляются также высшие гармоники (v > 1), порядок которых v не выражается целым числом.

Можно показать, что н. с. трехфазной дробной обмотки с фазной зоной 60° содержит гармоники

где k — любое такое положительное или отрицательное число (включая нуль), при котором v > 0.

Знак плюс в выражении (22-46) относится к прямым гармоникам (основная гармоника v = 1 является прямой и получается при k = 0), а знак минус — к обратным. При d = 1 (обмотка с целым q) равенство (22-46) определяет уже

Рис. 22-12. Кривая н. с. трехфазной двухслойной

дробной обмотки с Z = 30, 2р = 8, q = 1¹/₄, у — 0,8 т

(см. схемы рис. 21-5 и 21-7)

рассмотренные выше (см. § 22-2) гармоники н. с. обмотки с целым q [второе и третье равенства (22-29)]. При

Равенство (22-47) совпадает с (20-34), однако при q дробном v_z также дробное.

Н. с. трехфазных дробных обмоток, изображенных на рис. 21-5, 21-7 и 22-12 (2= 30,2р= 8,9= \^lU,d= 4), согласно выражению (22-46), содержат прямые гармоники v = 1, 2¹/_а. 4, 5^xk, 7, 8V2... и обратные гармоники v = V₂. 2, ЗУ₂, 5, б'/г-» При этом гармоники v = &/₃, 8¹/₂... являются гармониками зубцового порядка.

О вычислении обмоточных коэффициентов дробных обмоток см. в § 21-2.

В связи с тем что дробные обмотки создают магнитные поля с большим содержанием различных гармоник, которые вызывают ряд нежелательных явлений, их применение ограничено.

§ 22-4. Вращающиеся волны тока и линейной токовой нагрузки

Изменяющаяся вдоль поверхности якоря н. с. обмотки Ft является функцией координаты длины х, отсчитываемой от определенной точки поверхности якоря вдоль окружности В § 22-3 было показано, что кривая н. с. F_t — f(x) представляет собой интегральную кривую распределения тока обмотки »„ = ф(ж) вдоль окружности якоря, т. е.

При этом г_п — величина тока обмотки на единицу длины окружноети статора в некоторой точке этой окружности в определенный момент времени. В соответ-

ствии с этим кривая распределения тока оо-мотки является производной F*:

Интегрирование и дифференцирование синусоидальной функции приводит к синусоидальной же функции. Поэтому в соответствии с изложенным можно представить себе, что каждая гармоника н. с. Ff создается такой же гармоникой кривой распределения тока обмотки *'_п или синусоидальной пространственной волной тока, которая вращается синхронно с гармоникой н. с. (рис. 22 13)* Очевидно, что «_п можно представить себе как линейную плотность некоторого тока, распределенного по поверхности якоря.

Связь между угловой а и линейной х координатами вдоль окружности определяется зависимостью

Рис. 22-13. Синусоидальная волна пространственного распределения тока и создаваемая ею в<?лаа н. с.

или, согласно (22-35),

Величина У2 А равна амплитуде линейной нагрузки. В соответствии с выражением (22-53) амплитуда основной гармоники пространственной волны тока обмотки при k_ofy = 1 также равна амплитуде-линейной нагрузки. Очевидно, что

физически /_пт и Y2A представляют собой одну и ту же величину, а именно амплитуду величины тока обмотки на единицу длины окружности якоря. Вращающиеся волны то.ка поэтому можно назвать также вращающимися волнами линейной нагрузки. Величина fe_O6i входит в выражение (22-53) потому, что Л, согласно (22-33), вычисляется как средняя величина всего тока обмотки, а не его основной пространственной гармоники.

Выражения, аналогичные (22-51), (22-52) и (22-53), можно вывести и для других гармоник Ft и i_n.

Из изложенного следует, что получение идеальных кривых н. с. и магнитного поля, состоящих только из основных гармоник, возможно при условии, когда ток обмотки распределен вдоль окружности якоря синусоидально. Это было бы достижимо, если бы можно было намотать на гладкой поверхности якоря обмотку с числом фаз m -*■ со, фазные зоны которых суживаются до нуля вместе с углом сдвига токов соседних фаз. В реальных случаях распределение тока лишь грубо .приближается к синусоидальному, как видно из рис. 22-11, б и д. На этих рисунках штриховой линией показаны также кривые основной гармоники пространственной волны распределения тока, причем можно заметить, что эта гармоника вращается со скоростью основной гармоники н. с.

В большой степени ксинусоиде приближаются кривые н. с. и распределения тока в так называемых^синусйых обмотках. В этих обмотках витки распределяются по пазам неравномерно, по закону, приближающемуся к синусоидальному. Такие обмойси применяются в некоторых типах микромашин, в которых для достижения большой точности в работе необходимо всемерно подавлять н. с. и магнитные поля высших гармоник.

Отметим, что теорию электрических машин можно построить, исходя из рассмотрения указанных синусоидальных пространственных волн распределения тока и создаваемых ими магнитных полей.