I Поэтому электромагнитная связь в трансформаторах весьма высока, а рассеяние мало.

В силовых трансформаторах, например, с = 0,998 -*- 0,9995 и соответственно о = 0,001 ч- 0,004.

Вследствие этого значение а, определяемое по формуле (14-12), представляет собой разность весьма близких величин и вычисление а по этой формуле связано с весьма большими погрешностями, так как L_n, L_%% и М в практических устройствах не могут быть рассчитаны или определены из опыта с досхаточ-ной степенью точности. Поэтому возникает необходимость в непосредственном определении параметров, характеризующих электромагнитное рассеяние.

§ 14-2. Уравнения напряжения трансформатора

Рабочий процесс трансформатора можно исследовать на основе уравнений напряжения его обмоток.

Емкостные токи между элементами обмоток (витки и катушки) и между обмотками и сердечником трансформатора в обычных условиях работы трансформаторов (f < 1000 -f- 5000 гц) весьма малы, и ими можно пренебречь. В трансформаторах без ферромагнитного сердечника L_n, L₂₂ и М постоянны. В соответствии с изложенным в § 14-1 можно принять, что эти величины постоянны также для любого рассматриваемого режима работы трансформатора со стальным сердечником. Пренебрежем сначала магнитными потерями в сердечнике. Тогда для однофазного двухобмо-

точного трансформатора (рис. 14-2) действительны следующие уравнения напряжения в дифференциальной форме:

Рис. 14-2. Схема однофазного двухобмоточного трансформатора

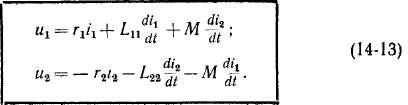
Здесь и_ъ и.₂, i_lt i₂ — мгновенные значения напряжения и тока первичной и вторичной обмоток; г_х, г._г, L_u, L₂₂ — активные сопротивления и собственные индуктивности обмоток; М — взаимная индуктивность обмоток.

На схеме рис. 14-2 указаны положительные направления и и i, причем стрелка и направлена от точки с высшим потенциалом к точке с низшим потенциалом.

При составлении уравнений (14-13) первичная обмотка рассматривается как приемник, а вторичная — как источник электрической энергии, и сами эти уравнения истолковываются следующим образом.

Первичное напряжение и_х является приложенным, расходуется на падение напряжения г^ и уравновешивание э. д. с. первичной обмотки

и состоит поэтому из двух составляющих: r_xi_x и — е_х, что и выражается первым уравнением (14-13). Вторичное напряжение и_% возникает вследствие индуктирования-во вторичной обмотке э. д. с.

что соответствует второму уравнению (14-13). В уравнениях (14-13) считается, что М > 0 и положительные токи i_x и i₂ создают в сердечнике потоки одинакового направления.

Отметим, что в правой части второго уравнения (14-13) можно было бы изменить знаки на обратные. Тогда и₂ следовало бы трактовать как напряжение, приложенное к вторичной обмотке со стороны вторичной сети. Некоторые, в особенности иностранные, авторы применяют также и эту последнюю форму записи.

Обычно силовые трансформаторы, а также ряд видов специальных трансформаторов работают с синусоидально изменяющимися токами и напряжениями. В этом случае вместо дифференциальных Уравнений (14-13) удобнее пользоваться комплексными уравнениями Для действующих значений токов и напряжений. Для получения этих уравнений в уравнения (14-13) следует подставить

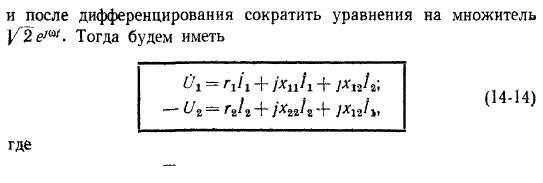
x_n — (nL_u; x_n = col₂₂; дг₁₂ = соМ                                                                                                                                                                                                                (14-15)

представляют собой полные собственные и взаимные индуктивные сопротивления обмоток.

При симметричной нагрузке трехфазных трансформаторов электромагнитные процессы протекают во всех фазах одинаково и соответствующие электромагнитные величины в каждой фазе также-одинаковы и лишь сдвинуты по фазе на 120°. Некоторая несимметрия магнитной цепи трехстержневого трансформатора, а также появление в ряде случаев (см. § 13-1) третьих гармоник потока обычно нет оказывают заметного влияния на работу трансформатора под' нагрузкой. К тому же эти .явления при необходимости можно учесть отдельно. По этим причинам уравнения (14-14) с большой точностью* применимы также для фазных величин трехфазного трансформатора при симметричной его нагрузке. Система уравнений (14-14)- не учи* тывает лишь потерь в стали сердечника трансформатора. Учет этиэ* потерь будет рассмотрен отдельно.

Для трехфазного трансформатора в соответствии со сказанным выше 0it U₂, /_х и /₂ представляют собой фазные значения напряжений и токов.

Уравнения (14-13) и (14-14) полностью определяют процессы происходящие в трансформаторе при указанных выше допущениях и позволяют решать задачи, связанные с работой трансформатора Например^если определить из первого уравнения (14-14) /_хи под ставить его значение во второе уравнение (14-14), то получим зав» симость вторичного напряжения 0_% от тока нагрузки 1_г:

а второй член — падение напряжения на вторичных зажимах npij нагрузке.

Из этих соотношений видно, что такие важные с эксплуатационной точки зрения величины, как падение напряжения и ток короткого замыкания, определяются небольшой долей а полного индуктивного сопротивления дг₂₂, обусловленной электромагнитным рассеянием. Это же можно сказать и о ряде других величий, характеризующих эксплуатационные свойства трансформаторов и вращающихся электрических машин. Поэтому определение величин, характеризующих электромагнитное рассеяние, составляет важную задачу теории электрических машин.

Кроме указанных соображений о точности результатов, расчеты ^на основе уравнений (14-13) и (14-14) неудобны также в связи с тем, ^Что ввиду неравенства чисел витков (w₁ Ф до₂) параметры r_lt г₂,

Ъ_п, L₂₂, М, х_п, х₂₂ и х₁₂, а также напряжения и_ъ и₂, U_lt U._z и токи <!, i₂, /₁₍ /₂ сильно различаются по величине.

В связи с изложенным теорию электрических машин в отношении рассматриваемых вопросов целесообразно развить в следующих тесно связанных друг с другом направлениях:

1.                       Индуктивно связанные обмотки приводятся путем-соответствующих пересчетов к одинаковому числу витков, е результате чего порядки напряжений, токов и параметров этих обмоток становятся соответственно одинаковыми.

2.                         Из полных собственных индуктивностей L_n, /_₂₂ и индуктивных сопротивлений самоиндукции х_п и х₂₂ выделяются составляющие — индуктивности рассеяния S_i} S₂ и индуктивные сопротивления рассеяния х_х и х_%, обусловленные явлением электромагнитного рассеяния, причем это выделение производится с таким расчетом, что остающиеся части полных индуктивностей (L_u — Si, L₂₂ — S₂) и индуктивных сопротивлений (хц — х_и ^Х22 — ^хй) соответствуют индуктивно связанным цепям с полной связью (с = 1).

3.                         Разрабатываются непосредственные методы расчета малых параметров — индуктивностей и индуктивных сопротивлений рассеяния — независимо от расчета полных индуктивностей и индуктивных сопротивлений, чем достигается необходимая точность в определении этих малых параметров.

4.                          От электрических цепей с индуктивной связью делается переход к схемам замещения с электрической связью цепей, что приводит к упрощению расчетов и большей наглядности теории.

5.                          Индуктивности и индуктивные сопротивления рассеяния вводятся в явном виде в расчетные соотношения и схемы замещения, что позволяет с необходимой точностью рассчитывать величины, зависящие от электромагнитного рассеяния.

Эти вопросы применительно к трансформаторам рассматриваются ииже.

§ 14-3. Схемы замещения двухобмоточного трансформатора

Приведение вторичной обмотки к первичной. Первичные и вторичные токи, напряжения и другие величины имеют одинаковый порядок, если у первичной и вторичной обмоток число витков одинаково. Рассмотрим поэтому вместо реального трансформатора эквивалентный ему так называемый приведенный трансформатор, первичные и вторичные обмотки которого имеют одинаковое число витков.

Представим себе, что реальная вторичная обмотка трансформатора с числом витков ш₂ заменена воображаемой, или приведенной,

обмоткой с числом витков w\ — Wx. При этом число витков вторичной обмотки изменится в

раз. Величина k называется коэффициентом приведения или трансформации.

В результате такой замены, или приведения, э. д. с. Е'₂ и напряжение U₂ приведенной обмотки также изменяются в k раз по сравнению с величинами £₂ и U₂ реальной вторичной обмотки:

Чтобы мощности приведенной и реальной обмоток при всех режимах работы были равны, необходимо соблюдать равенство

где 1'_% — приведенный вторичный ток. Отсюда с учетом второго равенства (14-21) следует, что

Намагничивающие силы приведенной и реальной обмоток на основании выражений (14-20) и (14-22) равны:

/>; = /_аш₂.                                                                                                                                                                                                                                                                                                                                                                                                                                     (14-23)

Для того чтобы электромагнитные процессы в реальном и приведенном трансформаторах протекали одинаково, приведенная и реальная вторичные обмотки должны создавать одинаковые магнитные поля. Для этого, кроме соблюдения условия (14-23), необходимо, чтобы приведенная вторичная обмотка имела те же геометрические размеры и конфигурацию и была расположена в окне сердечника трансформатора так же, как и реальная вторичная, обмотка (см. например, рис. 12-2, 12-26). Поэтому суммарное сечение всех витков приведенной обмотки должно быть таким же, как и у реальной обмотки, а сечение каждого витка приведенной обмотки должно уменьшиться в k раз. Но поскольку приведенная обмотка имеет в k раз больше витков, то в итоге активное сопротивление приведенной обмотки в k² раз больше, чем реальной:

Так как при одинаковых геометрических размерах и одинаковом расположении катушек их индуктивности и индуктивные сопротивления пропорциональны квадратам чисел витков, то между индуктивными сопротивлениями приведенной обмотки х'₃ и реальной лг₂ существует такое же соотношение:

Таким образом, все энергетические и электромагнитные соотношения в приведенном и реальном трансформаторах одинаковы, что и позволяет производить указанное приведение.

Схема замещения без учета магнитных потерь. В соответствии с изложенным сделаем в уравнениях напряжения трансформатора (14-14^ поястановки:

При переходе к электрической связи двух цепей в соответствующей схеме замещения должна появиться общая для обеих цепей ветвь, которая обтекается суммой токов обеих цепей /_г + 1[. Соответственно этому в уравнениях напряжений этих цепей должны появиться одинаковые члены с множителями (/_х + /J). Из уравнений (14-27) видно, что для получения в них таких членов нужно прибавить к первому из этих уравнений и вычесть из него член ]кх_п!_г и прибавить ко второму и вычесть из него член ]кх_п{'_%. При этом получим

Введем следующие наименования и обозначения: