Задание и отчетность

1. Ознакомиться с теоретическим описанием к данной работе.

2. Нажать рукоятку (7) вниз до отказа и подложить под рычаг (6) подставку из теплоизоляционного материала с таким расчетом, чтобы после опускания рукоятки стержень (3) не касался основания (1).

3. Включить нагревательный элемент в осветительную сеть с напряжением 220 вольт. При этом переключатель вида измерений должен стоять в положении "температура". Дождаться, когда разность температур между стержнем и основанием достигнет 20°С (рис. 2.26).

4. 4. Не отключая нагреватель от сети, быстро пинцетом подложить образец под стержень и, нажимая на рукоятку (7), убрать подставку под рычагом (6).

5. 5. Установить индикатор переключателем в положение "ТЭДС" и опустить рукоятку (7). При этом стержень должен плотно прижать образец к основанию.

6. Записать показание прибора по верхней шкале, нажать рукоятку (7) вниз и подпереть рычаг. Переключить индикатор в положение "температура" и ждать, пока разность температур не достигнет 40°С. Образец сдвинуть в сторону.

7. Повторить пункты 4, 5 и 6, но ждать, пока разность температур не достигнет 60°С.

8. Проделать то же самое при разности температур в 80°С и 100°С.

9. Для каждого случая найти коэффициент термоэдс как результат деления разности потенциалов на разность температур.

10. Результаты всех измерений и вычислений занести в таблицу.

Таблица 2.6

ΔE
ΔT
α
ζ

Для каждого значения αвычислить потенциал Фермиζи занести в таблицу.

11. Найти среднее значение потенциала Ферми , подсчитать абсолютную и относительную ошибки.

Контрольные вопросы

1. В чем заключается эффект Зеебека?

2. Что представляет собой эффект Пельтье?

3. В чем сущность эффекта Томсона?

4. Какова связь между коэффициентами Зеебека, Пельтье, Томсона?

5. Какова связь между коэффициентом термоэдс и потенциалом Ферми?

Литература [3] 7.1, 7,2; [5] 9.79-9.81; [6] 9.1-9.4.

Рис 2.26. График перевода эдс термопары в температуру

2.5. Определение коэффициента Пельтье компенсационным методом

Цель работы:ознакомление с эффектом Пельтье и методами охлаждения радиоаппаратуры с помощью полупроводниковых термобатарей.

Основные сведения из теории

ЭффектомПельтьеназывается явление, заключающееся в том, что при прохождении тока в цепи, состоящей из разнородных материалов, в одном из контактов выделяется сверх джоулевой теплоты дополнительная теплота (теплота Пельтье), а во втором контакте теплота поглощается. В результате этого температуры спаев оказываются различными. При изменении направления тока холодный и горячий спаи меняются местами.

Таким образом, нетрудно заметить, что это явление обратно явлению возникновения термоэдс при нагревании или охлаждении одного из спаев двух разнородных металлов, получившему название эффекта Зеебека. Оба явления тесно связаны друг с другом. Если эффект Зеебека записывается в виде формулы:

, (2.56)

где ε– термоэдс;

T₁,T₂ – температуры спаев;

α – коэффициент Зеебека (коэффициент ТЭДС), то эффект Пельтье можно записать как:

, (2.57)

где Q_П– теплота Пельтье;

I – ток в цепи;

t – время прохождения тока;

П– коэффициент Пельтье .

Между коэффициентами Пельтье и Зеебека существует простое соотношение:

, (2.58)

где Т– абсолютная температура соответствующего спая.

Первоначально оба явления были обнаружены на спаях разнородных металлов, но в дальнейшем оказалось, что в полупроводниках эти явления достигают гораздо больших значений. Благодаря этому академиком А.Ф. Иоффе была доказана возможность практического применения эффекта Пельтье.

В полупроводниках наибольшими коэффициентами термоэдс обладают термопары, составленные из материалов разной проводимости, т.е. из полупроводников n-типа и р-типа. При этом рабочие характеристики термоэлемента зависят не от его конструкции, а только от свойств материалов, из которых изготовлены ветви. В связи с этим важно знать, при каких соотношениях параметров материалов термоэлемент обладает максимальной эффективностью.

Если от нагревающегося спая тепло отводить, т.е. поддерживать его при постоянной температуре, то другой спай будет еще сильнее охлаждаться, сохраняя некоторую разность температур по сравнению с первым спаем. Можно выявить условия, при которых эта разность будет максимальной.

Любой термоэлемент состоит из последовательно соединенных ветвей с электронной и дырочной проводимостями (рис. 2.27).

Рис. 2.27. Простейший термоэлемент

Для простоты можно считать, что в интервале температур T₁–T₂, коэффициенты термоэдс каждой ветви постоянны. Кроме того, будем считать постоянными коэффициенты теплопроводимости () и электропроводимости ( ), а также примем равными геометрические размеры ветвей ( ).

Когда по термоэлементу проходит ток, температура спая 1 понижается до некоторого значения. При заданном токе Iвеличина понижения температуры зависит не только от поглощаемого тепла Пельтье, но и от тепловой нагрузки на этом спае, которая складывается из теплопритока от окружающей среды и тепла от спая 2, обусловленного теплопроводностью ветвей и теплоты Джоуля, выделяющейся в ветвях при прохождении тока. В этих условиях существенное влияние на работу термоэлемента оказывает теплота Джоуля, так как она пропорциональна квадрату тока.

Было доказано, что около половины теплоты Джоуля приходится на горячий спай и столько же на холодный. Это уменьшает эффект охлаждения холодного спая.

На рис. 2.28 представлено графически соотношение теплот на холодном спае. Из этого графика видно, что наибольшее охлаждение получается при некотором оптимальном значении тока I_опт который можно рассчитать из уравнения теплового баланса для холодного спая. Действительно, если на холодный спай термоэлемента приходится количество теплоты

(2.61)

где R– сопротивление термоэлемента, то, дифференцируя это уравнение по току и приравнивая производную к нулю, находим, чтоQдостигает максимума при оптимальном токе

, (2.62)

откуда

. (2.63)

Знак "минус" показывает, что преобладает поглощение тепла.

Рис. 2.28. Зависимость количества теплоты Пельтье (Q₂) и Джоуля (Q₁), поступающей на холодный спай, от токаI

В стационарном состоянии теплота должна компенсировать тепловую нагрузку холодного спая, т.е. приток тепла извне и тепло, приходящее от спая 2 за счет теплопроводности:

. (2.64)

Таким образом,

. (2.65)

Из этого уравнения можно определить максимальную разность температур, если считать, что холодный спай идеально изолирован от окружающей среды, т.е. Q₀= 0.

Тогда

, (2.66)

где l,S– длина и площадь сечения.

Откуда

. (2.67)

Если учесть, что П=α·tи, то

. (2.68)

В этой формуле величина обозначается буквойz и носит название эффективности термоэлемента. Следовательно,

. (2.69)

Отсюда видно, что максимально достижимая разность температур зависши не от конструкции термоэлемента, а только от свойств материала, т.е. от тех параметров, которые входят в выражение для z.

Величина zпредставляет собой меру добротности материалов. Поэтому усилия исследователей в области термоэлектричества направлены на изыскание материалов с большимz. Параметры веществ (), входящие в числоzзависят от концентрации свободных носителей тока (электронов и дырок).

Теоретически была получена формула для определения оптимальной концентрации носителей:

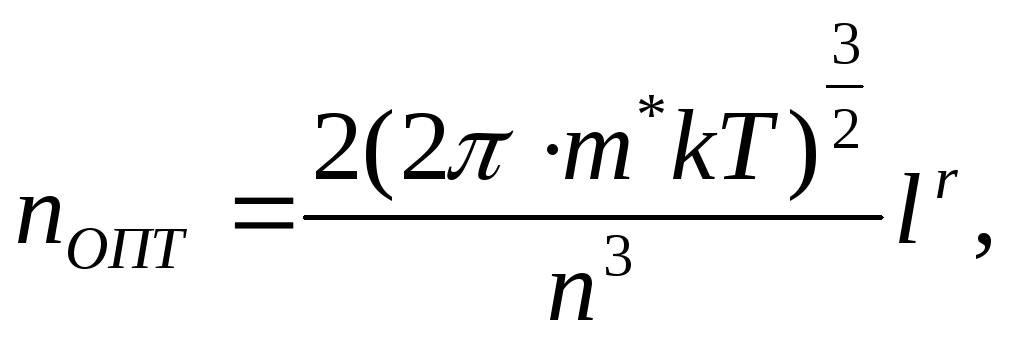(2.70)

где m^*– эффективная масса электрона;

r – показатель, характеризующий механизм рассеяния носителей.

Для максимального значения zполучена формула:

(2.71)

где μ– подвижность носителей;

λ_р– теплопроводность решетки;

m₀ – масса свободного электрона.

Из этой формулы следует, что величина z пропорциональна отношению подвижности носителей к теплопроводности решетки. Таким образом, материал для ветвей термоэлемента должен удовлетворять следующим требованиям:

1). иметь оптимальную концентрацию носителей;

2). обладать максимальным отношением подвижности носителей к теплопроводности решетки.

Этим условиям наиболее соответствуют в настоящее время твердые растворы Bi₂Tl₃ + Bi₂Se₃ (для отрицательной ветви) иBi₂Tl₃ + Sb₂Tl₃ (для положительной ветви).