Определители высших порядков.

Все перечисленные выше свойства дословно переносятся на определители любого порядка. При их вычислении основную роль играют свойства 7 и 8. С помощью свойства 7 добиваются того, чтобы в некоторой строке стояли на всех местах нули, кроме, может быть, одного. Затем, применяя свойство 8, разлагают определитель по этой строке и тем самым сводят его вычисление к нахождению определителя меньшего порядка. Повторяя этот прием, в конце концов, получают определитель второго или третьего порядка, который вычисляется непосредственно. Разумеется, вместо строк можно выбрать столбцы, используя свойство их равноправности.

Примеры решения задач

3. Вычислить определитель четвертого порядка

.

Решение: В данном случае удобно из четвертой строки вычесть

третью, тогда в ней получится сразу три нуля

.

Разлагая теперь определитель по четвертой строке, мы должны будем умножить ее элементы на свои алгебраические дополнения и результаты сложить. Но поскольку три из четырех этих элементов равны нулю, то из всей суммы остается лишь второе слагаемое

Выписанный минор получен из определителя  вычеркиванием второго элемента четвертой строки. Алгебраическое дополнение этого элемента равно минору, умноженному на (-1)⁴⁺² = 1. Определитель третьего порядка, который получился, вычислен непосредственно.

Метод приведения к треугольному виду заключается в таком преобразовании определителя, когда все элементы, лежащие по одну сторону одной из его диагоналей, становятся равными нулю.

Вычислить определитель:

Решение: Вычитая первую строку из всех остальных, получаем:

Упражнения

Вычислить определители:

1. ; 2.; 3.;

4. ; 5.; 6.;

7. 8..

Высшая алгебра.

Матрицы и определители.

Понятие матрицы и основанный на нём раздел математики – матричная алгебра – имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей, экономических объектов и процессов записываются в достаточно простой, а главное – компактной матричной форме.

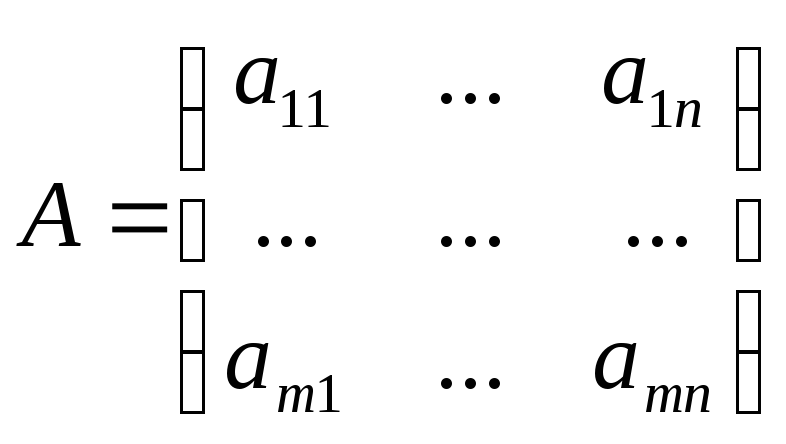
Матрицей называется система элементов (в частном случае чисел), находящихся в определённом порядке и образующих таблицу. Если в этой таблице m строк и n столбцов, а её элементы обозначены через a_ij, где i – номер строки, а j – номер столбца, на которых находится этот элемент, то матрица записывается в следующем виде:

. (1)

Короче эта матрица может быть записана так: А = (а_ij), (i = 1, m; j = 1, n). Каждый элемент матрицы называется её компонентой.

Матрица (1) имеет размер mn. Если число строк матрицы m не равно числу её столбцов n, то матрица называется прямоугольной. Если число строк равно числу столбцов, то матрица называется квадратной, тогда говорят о порядке матрицы. Матрица, у которой все элементы равны нулю, называется нулевой. Квадратная матрица, у которой равны нулю все элементы, кроме элементов, стоящих на главной диагонали, называется диагональной. Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной, и обозначается через I или Е. Иногда применяется транспонирование матрицы А, т.е. перемена ролями её строк и столбцов. Полученную матрицу обозначают через А^Т. В общем, виде можно написать а^Т_ij = а_ji. Ясно, что (А^Т)^Т = А.

Матрица, совпадающая со своей транспонированной, называется симметричной; (такой может быть только квадратная матрица). Условие симметричности можно записать в виде

Квадратная матрица А имеет определитель, который мы будем обозначать Прямоугольная матрица определителя не имеет, так как определители бывают только квадратные (Определителем n-го порядка называется число, которое обозначается:

.

Если из определителя квадратной матрицы порядка n вычеркнуть i-ую строку и j-ый столбец, на пересечении которых стоит элемент, и составить из оставшихся элементов определитель порядка n -1, умножив на (-1)^i+j, где I + j – сумма номеров вычеркнутой строки и столбца, то полученное произведение называется алгебраическим дополнением элемента матрицы и обозначается символом A_ij. Минором М_ij элемента a_ij матрицы n-го порядка называется определитель матрицы (n -1) порядка, полученный из матрицы А вычёркиванием i-й строки и j-го столбца:

,

т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца (i+j)-чётное число и не совпадает, когда (i+j) – нечётное число.

Формула для вычисления определителей:

. (4.14)

Предполагается, что а₁₁  0, если а₁₁ = 0, то перестановкой строк и столбцов всегда можно из данного определителя получить такой, в котором = 0. Эта формула очень проста в употреблении и позволяет вычисление определителя порядка n свести к вычислению определителя порядка n - 1.

Действия над матрицами:

Линейными действиями над матрицами называется сложение матриц и умножение их на число. Оба эти действия определяются поэлементно:

Сложению матриц имеет обратное действие – вычитание, которое также осуществляется поэлементно, например, если А = (а_ij),

В = (b_ij), то С = А - В = (c_ij), где c_ij.= a_ij – b_ij .

Отметим очевидные формулы:

(А + В)^T = А^T + В^T; (kА)^T = kА^T; det(kC) = kⁿdetC,

где n – порядок квадратной матрицы С. При этом, вообще говоря, det(A+B)  detA + detB.

Пример:

,

Умножение матриц:

,

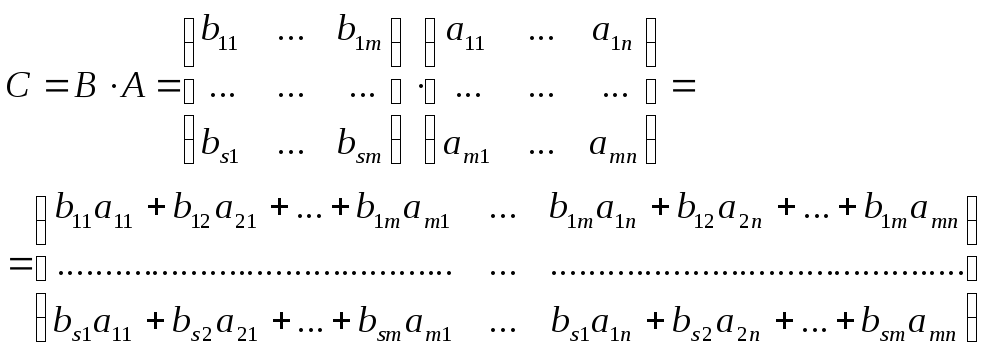
Матрица С называется произведением матрицы В на матрицу А. С = ВА. Размер её (sm)  (mn) = (sn).

Элемент матрицы С, стоящий в i –ой строке и j –ом столбце, равен сумме произведений элементов i-ой строки матрицы В на соответствующие элементы j –ого столбца матрицы А, т.е.

,

(т.е. для нахождения элементов произведения матриц В и А мы находим скалярное произведение i строки матрицы В на j столбец матрицы А).

Пример

, .

.

Откуда видно, что ВА  АВ.

Свойства произведения двух матриц:

А) Не всякие две матрицы можно перемножить. Произведение ВА двух матриц в указанном порядке возможно в том и только в том случае, если число столбцов матрицы В равно числу строк матрицы А (ширина первого сомножителя должна равняться высоте второго). Символически это можно записать так: (mk)  (kn).

Значит, в матрице, являющейся произведением двух матриц, число строк равно числу строк левого сомножителя, а число столбцов – числу столбцов правого сомножителя.

Простое правило, определяющее возможность матричного умножения и его результат, можно записать следующим образом (здесь А – матрица порядка mk, В - kn): (mk)*(kn)

(порядок произведения).

Таким образом, произведение матрицы определено только в том случае, когда внутренние индексы равны. Тогда порядок произведения получается вычёркиванием внутренних индексов.

Очевидно, что порядок, в котором перемножаются матрицы (здесь мы не можем избежать использования слова “порядок” в двух смыслах), имеет решающее значение. В произведении ВА тех же матриц А и В мы имели бы (kn)  (mk). Внутренние индексы здесь не равны, т.е. произведение ВА не определено.

Если А – матрица порядка mn, а В – порядка nm, то определены оба произведения АВ и ВА. Однако АВ будет матрицей порядка mn, в то время как ВА - nm, т.е. АВ = ВА. Только тогда, когда А и В – квадратные матрицы одного и того же порядка, возможно равенство АВ = ВА, но даже и в этом случае оно, вообще говоря, не верно.

Б) Произведение двух матриц, в общем случае, не обладает свойством переместительности (т.е. иначе говорят, что не обладает свойством коммутативности).

Значит, в общем случае менять местами матрицы – сомножители нельзя, не изменив их произведения. В этом состоит одно из отличий законов алгебры матриц от законов элементарной алгебры. Если изменить порядок сомножителей, может оказаться, что вообще умножить матрицы невозможно.

В произведении ВА двух матриц В и А мы будем говорить, что матрица А умножается слева на матрицу В, или что матрица В умножается справа на матрицу А.

Правило умножения матриц на первый взгляд может показаться громоздким и сложным. Однако, те кому приходится часто и много работать с матрицами, очень быстро привыкают безошибочно это правило применять, и оно представляется им исключительно простым; палец левой руки должен скользить слева направо вдоль строк первой матрицы, а палец правой руки должен при этом скользить по столбцам второй матрицы сверху вниз. Выполнив несколько упражнений, правило умножения матриц можно легко освоить.

Если две матрицы А и В – квадратные одного и того же порядка, а их произведение АВ есть единичная матрица АВ=Е, то матрица В называется матрицей обратной к А и обозначается символом А^-1. Следует иметь в виду, что квадратная матрица А и ей обратная А^-1 коммутативны, т.е. АА^-1 = А^-1А = Е.

Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы определитель А(detA) не был равен нулю, т.е. матрица А не должна быть особенной (вырожденной).

Укажем основные методы вычисления обратной матрицы:

А) Метод присоеднённой матрицы

(если А невырожденная матрица)

Матрица , элементами которой является алгебраические дополнения оответствующих элементов матрицы А, называется присоединённой (в литературе присоеднённую матрицу называют взаимной, или союзной) к матрице А

Справедливо равенство ()^ТА = A()^Т = detAЕ

Отсюда следует, что если А – невырожденная матрица, то

А^-1 = (1/ detA)  ()^Т. (2)

Приведём алгоритм вычисления обратной матрицы.

1. Находим определитель исходной матрицы. Если detA = 0, то матрица А – вырожденная и обратной матрицы А^-1 не существует. Если detA  0, то матрица А – невырожденная и обратная матрица существует.

2. Находим алгебраические дополнения соответствующих элементов матрицы А, и составляем из них присоеднённую матрицу .

3. Вычисляем обратную матрицу по формуле (2)

4. Проверяем правильность вычисления обратной матрицы

А^-1, исходя из её определения А^-1А = AА^-1 = Е.

Найти матрицу, обратную к данной:

.

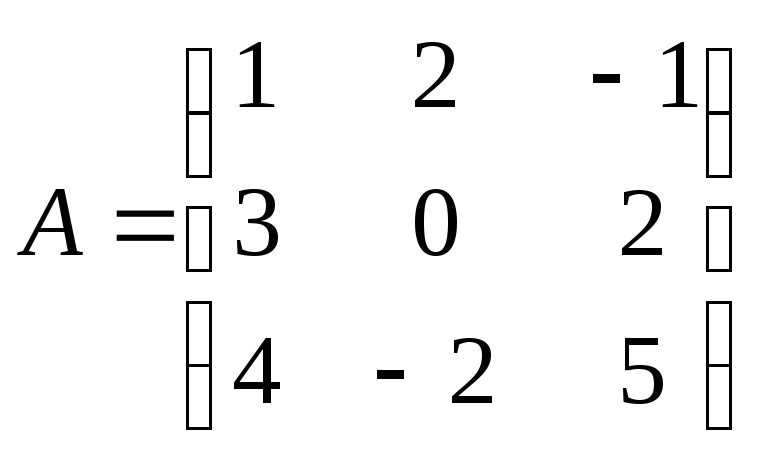Решение:

1. Определитель матрицы detA = - 4  0, значение определителя получено разложением по первой строке:

2. Находим алгебраические дополнения соответствующих элементов матрицы А:

и составляем из них присоединённую матрицу :

3. Находим матрицу (А^v)^Т, транспортированную к А^v

4. Вычисляем обратную матрицу по формуле

.

5. Проверяем правильность вычисления обратной матрицы по формулам: А^-1А = AА^-1 = Е

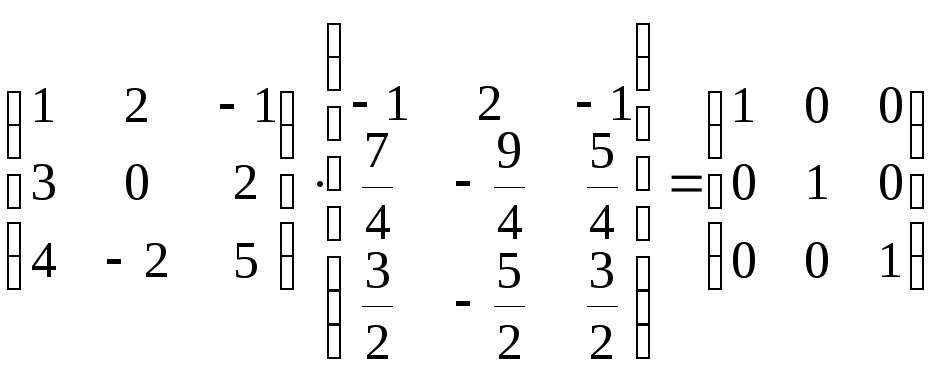(Проверьте!)

Методом элементарных преобразований найти А^-1 для

заданной матрицы:

Решение: образуем матрицу Г_А:

Обозначим через , строки матрицы Г_А, произведём над ними следующие преобразования:

В результате последовательно получаем

Следовательно,

.

Для невырожденных матриц выполняются следующие свойства:

1. detА^-1 = (1/ detA); 2. (А^-1)^-1 = A; 3. (А^m)^-1 = (А^-1)^m;

4. (АB)^-1 = B^-1A^-1; 5. (А^-1)^T = (А^T)^-1.

В) Вычисление обратной матрицы методом элементарных преобразований (метод Гаусса).

Напомним, что элементарными преобразованиями матрицы называются следующие: 1) перестановка строк (столбцов) 2). Умножение строки (столбца) на число, отличное от нуля; 3). Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.

Алгоритм вычисления обратной матрицы методом Гаусса состоит в следующем преобразовании: Для данной матрицы А n-го порядка построим прямоугольную матрицу Г_А = (АЕ) размера n2n, приписывая к А справа единичную матрицу. Далее, используя элементарные преобразования над , приводим матрицу Г_А к виду (ЕВ), что всегда возможно, если А невырождена. Тогда В=А^-1 (коротко, это выглядит так ((АЕ)  (ЕА^-1)), элементарные преобразования осуществляются только над строками).

Примеры решения задач

1. Пусть

, ,.

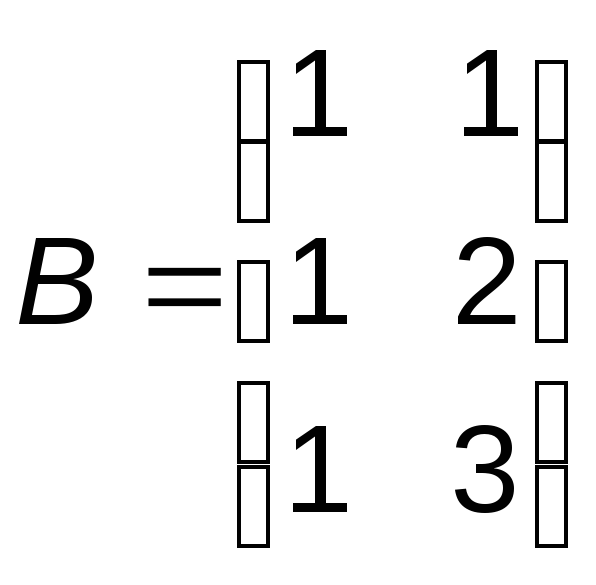Вычислить АВ, ВА, АС, ВС и С².

Решение:

.

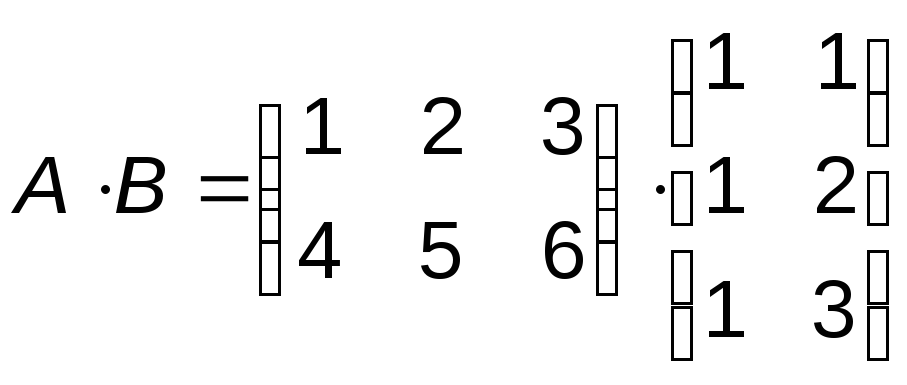Видим, что количество столбцов у матрицы А, равно количеству строк у матрицы В, следовательно произведение матриц существует. Найдём рамер этой матрицы: (23)  (32) = (22). Найдём произведение матриц:

.

Аналогично,

.

Далее,

и

.

Произведение ВС не определено, так как число столбцов матрицы В (два) не равно числу строк матрицы С (три), т.е. ширина матрицы В не равна высоте матрицы С.

2. Вычислить произведение матрицы строки на матрицу столбец:

.

Очевидно, правило произведения выполнено и размер произведения: (15)(51) = (11) т. е. получим число:

.

3. Вычислить:

.

Решение: выполняя последовательно произведение матриц, получим:

,

.

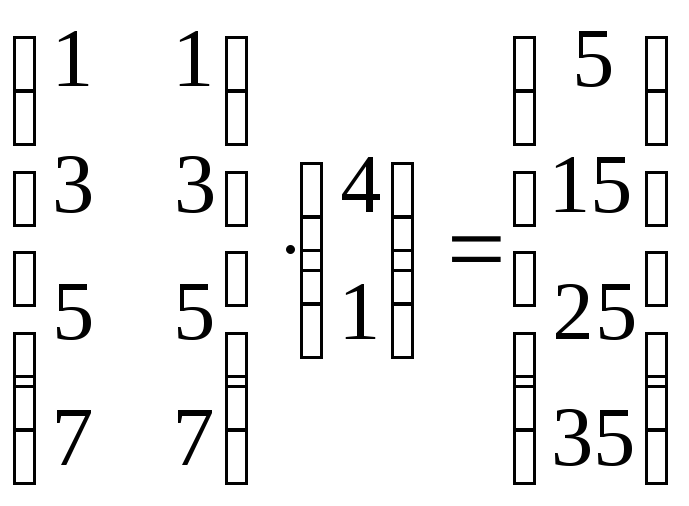4. Вычислить обратные матрицы для следующих матриц:

а) ;b) .

Решение:

а)

Вычтем из третьей строки первую и вторую строки и вычтем из второй строки первую, тогда

Наконец, вычтем из первой строки вторую и третью, умноженную на ½, и разделим третью строку на 2, тогда

.

Проверка: А^-1А = АА^-1 = Е

.

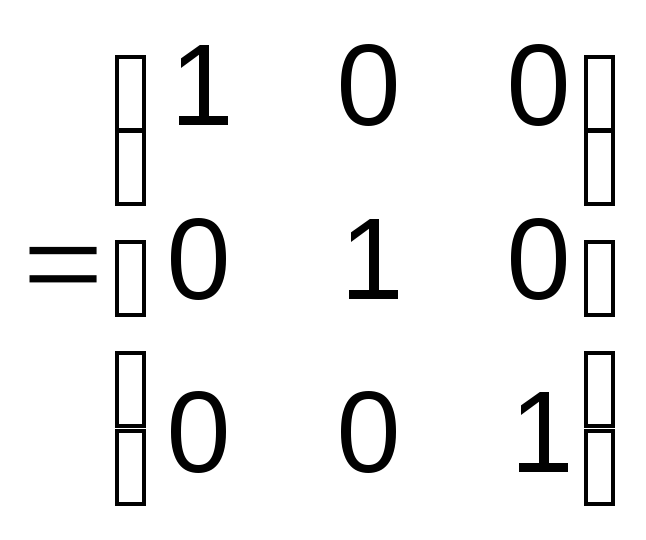b)

вычтем четвёртую строку из третьей и разделим четвёртую строку на 2, тогда

теперь вычтем из первой строки удвоенную вторую, а затем третью строку, умноженную на 6, и вычтем из второй строки удвоенную третью.

.

В справедливости этих выкладок убедиться, сделав проверку умножением исходной матрицы на полученную обратную.

5. Даны матрицы

.

Решить уравнения:

а) AX = B; b) XA = C

Решение:

1. AX = B Выразим из этого уравнения X. Для этого его слева умножим на А^-1.

A^-1АX = A^-1B  X = A^-1B (размер (22)  (23) = (23)).

Найдём обратную матрицу А^-1, (А^-1 = (1/ detA)  (А^v)^Т!)

согласно алгоритму вычисления обратной матрицы:

1. detA = 31 - 21 = 1, так как detA  0, то А^-1 существует.

2. Находим алгебраические дополнения соответствующих элементов матрицы А и составляем из них присоеднённую матрицу : = 1, = -1, = -2, = 3 ^:

.

3. Находим матрицу (^Т, транспонированную к ),

.

4. Вычисляем обратную А^-1=(1/ detA)  ()^Т:

5. Проверяем правильность вычисления обратной матрицы

А^-1 , исходя из её определения А^-1А = AА^-1 = Е

.

Матрицу неизвестных Х найдём, умножая уравнение слева на А^-1:

.

б) Полагая матрицу А невырожденной, умножим обе части уравнения XA = C справа на обратную матрицу А^-1: (XA)А^-1 = CА^-1 . Так как (XA)А^-1 = X(AА^-1) = XE = X, то X = СА^-1 и размер матрицы переменных (42); (так как (42)(22) = (42)):

.

Следовательно,

Ответ:

.

5. Решить уравнение:

.

Решение: обозначив:

,

представим уравнение в виде АXВ = С. Умножим обе части уравнения слева на обратную матрицу А^-1 и справа на обратную матрицу В^-1, учитывая, что А и В – невырожденные матрицы:

detA = 1  0, detB = -10  0. Получим А^-1(АXВ)В^-1 = А^-1СВ^-1. Учитывая, что А^-1(АXВ)В^-1 = (А^-1А) (XВ)В^-1 = Е(XB)В^-1 = (XB)В^-1 = X(BВ^-1) = XE = X, получим X= А^-1СВ^-1

Теперь найдём

.

Поэтому

.

Ответ: .

Упражнения

1. Вычислить линейные комбинации матриц и 3А + 2В; В – 3А; 2(А – В), если

и .

2. Вычислить произведения матриц:

а) ; б);

в) ; г);

д) ; е).

3. Методом присоедненной матрицы найти обратные для следующих матриц:

а) ; б); в);

г) ; д).

4. Методом элементарных преобразований найти обратные матрицы для следующих матриц:

а) ; б); в);

г) .

5. Вычислите А^-1, B^-1, AB и (АB)^-1, если

,,

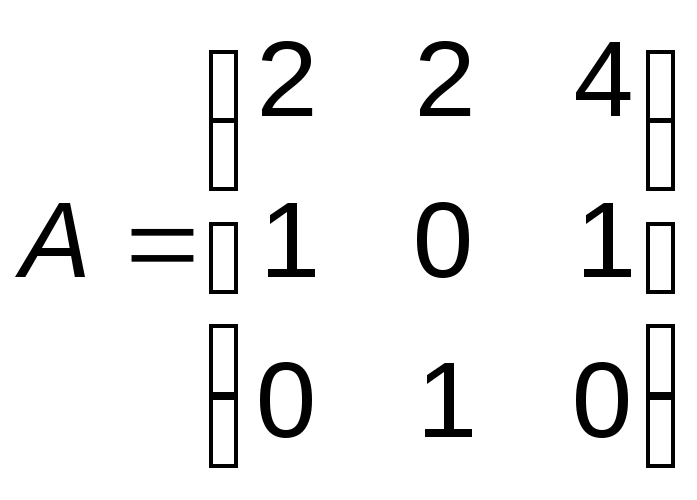убедитесь в том, что (АB)^-1 = B^-1А^-1 .

6. Решить матричные уравнения:

а) ;б);

в) ;

д) ;

е) .

Системы линейных алгебраических уравнений (СЛАУ).

Это один из основных разделов в алгебре. Нет такой отрасли науки и приложений, где в том или ином виде не использовались бы системы линейных алгебраических уравнений. При решении экономических и управленческих задач системы линейных уравнений наиболее употребимы как в аппарате исследования, так и при рассмотрении частных проблем.

Система m линейных уравнений с n неизвестными (переменными) x₁, x₂, . . . , x_n имеет вид

, (1)

где (i=1,2...m; j=1,2...n) - произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.

В более краткой записи с помощью знаков суммирования систему можно записать в виде:

.

Решением системы называется такая совокупность n чисел

(), при подстановке которых каждое уравнение системы обращается в верное равенство.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Две системы уравнений называются равносильными, или эквивалентными, если одно и то же множество решений.

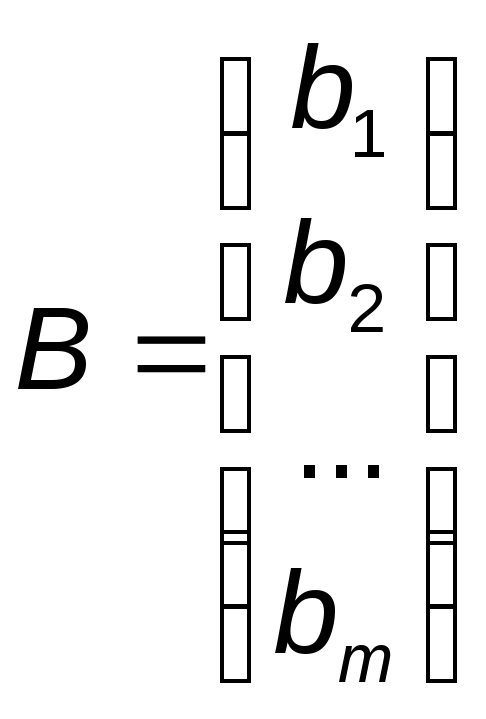
Запишем систему (1 в матричной форме). Обозначим

,

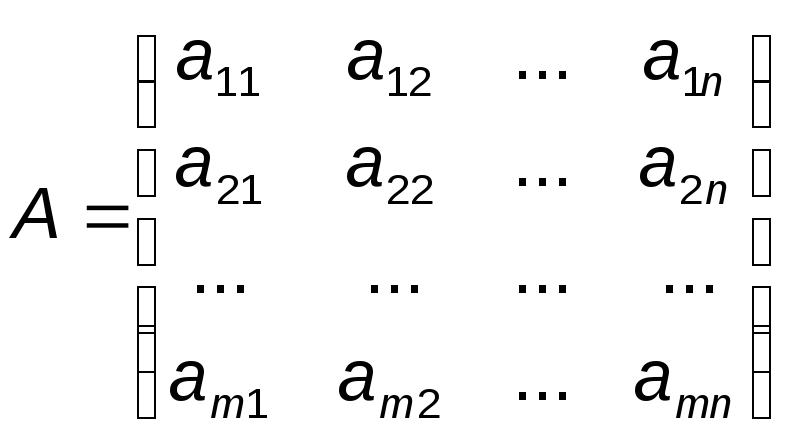
где А – матрица коэффициентов при переменных, или матрица системы; Х – матрица-столбец переменных; В – матрица-столбец свободных членов.

На основании определения равенство (1) можно записать в виде:

AX = B (2)

Система n линейных уравнений с n переменными. Метод обратной матрицы и формулы Крамера.

Пусть число уравнений системы (1) равно числу неизвестных, (переменных), т.е. m = n. Тогда матрица системы является квадратной, а ее определитель detA называется определителем системы.

Для получения решения системы (1) при m = n в общем виде предложим, что квадратная матрица А невырoждена, т.е. её определитель detA  0. В этом случае существует обратная матрица A^-1. Умножая слева обе части матричного равенства (2) на матрицу A^-1, получим A^-1(AX) = A^-1B. Так как A^-1(AX) = (A^-1A)X = EX = X, то решением системы методом обратной матрицы будет матрица-столбец X = A^-1B.

Пусть ∆ - определитель матрицы системы , а ∆_i - определитель матрицы, получаемой из матрицы заменой i-го столбца столбцом свободных членов. Тогда, если ∆  0, то система имеет единственное решение, определяемое по формулам

Формулы получили название формул Крамера.

Пример 1. Решить систему уравнений по формулам Крамера.

.

Решение: Найдём определитель системы

.

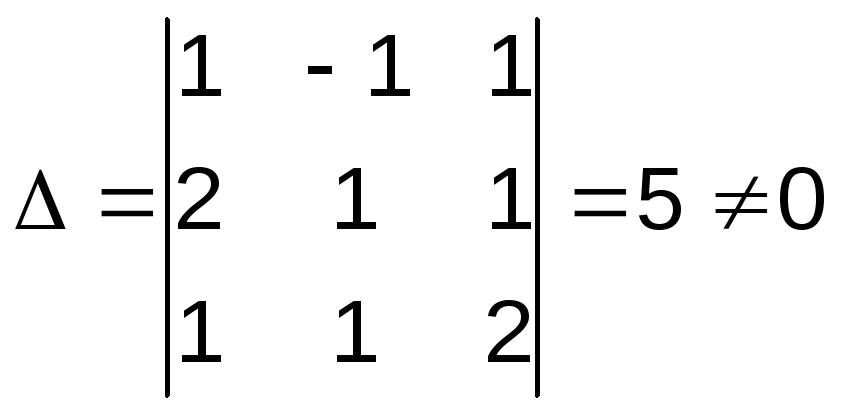Так как ∆  0, то по правилу Крамера система имеет единственное решение. Вычислим определители матриц ∆, ∆, ∆, полученные из матрицы А, заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:

(рекомендуем читателю вычислить самостоятельно!). Теперь по формулам Крамера найдём решения системы:

.

Ответ: .

Существенным недостатком решения систем и линейных уравнений с n переменными по формулам Крамера и методом обратной матрицы является их большая трудоёмкость, связанная с вычислением определителей и нахождением обратной матрицы. Поэтому эти методы представляют скорее теоретический интерес и на практике не могут быть использованы для решения реальных экономических задач, сводящихся часто к системам с большим числом уравнений и переменных.

Метод Гаусса.

Рассмотрим решение системы (1) m линейных уравнений с n переменными в общем виде.

Метод Гаусса – метод последовательного исключения переменных- заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Предположим, что в системе (1) коэффициент при переменной x в первом уравнении a  0 (если это не так, то перестановкой уравнений местами добьёмся того, что a  0).

. Умножая первое уравнение на подходящие числа (a, именно, на -a/a, - a/a, . . . , a/a), и прибавляя полученные уравнения соответственно ко второму, третьему, ..., m-му уравнению системы (1), исключим переменную х₁ из всех последующих уравнений, начиная со второго.

Получим:

.

Где буквами с верхним индексом (1) обозначены новые коэффициенты, полученные после первого шага.

. Предположим, что (если это не так, то соответствующей перестановкой уравнений или переменных с изменением их номеров добьёмся того, чтобы).

Умножая второе уравнение на подходящие числа

(,, . . . ,) и прибавляя полученные уравнения соответственно к третьему, четвёртому, ... ,m-му уравнению системы, исключим переменную x из всех последующих уравнений, начиная с третьего.

Продолжая процесс последовательного исключения переменных x, x, ... , x, после (r-1)-го шага получим систему

(4)

Число нуль в последних m-r уравнениях означает, что их левые части имеют вид 0+ 0+...+ 0. Если хотя бы одно из чисел b, .... , не равно нулю, то соответствующее равенство противоречиво, и система (1) несовместна.

Таким образом, для любой совместной системы числа b, .... , в системе (4) равны нулю. В этом случае последние m+r уравнений в системе (4) являются тождеством и их можно не принимать во внимание при решении системы (1). Очевидно, что после отбрасывания « лишних» уравнений возможны два случая: а) число уравнений (4) равно числу переменных, т.е. r = n ( в этом случае система имеет треугольный вид); б) r < n ( в этом случае система (4) имеет ступенчатый вид).

Переход системы (1) к равносильной ей системе (4) называется прямым ходом метода Гаусса, а нахождение переменных из системы (4) – обратным ходом.

Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов. Рассмотрим матрицу

называемую расширенной матрицей системы (1), ибо в неё, кроме матрицы системы А, дополнительно включен столбец свободных членов.

ПРИМЕРЫ.

2. Решить систему уравнений

Решение. Расширенная матрица системы имеет вид:

.

ШАГ 1. Так как  0 то, умножая первую строку матрицы на числа (-2), (-3), (-2) и прибавляя полученные строки соответственно ко второй, третьей, четвёртой строкам, исключим переменную . из всех строк, начиная со второй. Заметив, что в новой матрице = 0, поменяем местами вторую и третью строки:

.

ШАГ 2. Так как теперь = - 4  0 то, умножая вторую строку на (-7/4) и прибавляя полученную строку к четвёртой, исключим переменную из всех строк, начиная с третьей:

.

ШАГ 3. Учитывая, что = -8  0, умножаем третью строку на 13,5 / 8 = 27 / 6, и, прибавляя полученную строку к четвёртой, исключим из неё переменную .

Получим систему уравнений

.

Откуда, используя обратный ход метода Гаусса, найдём из четвёртого уравнения из третьего из второго и из первого уравнения т.е. решение системы (1,2,-1,2).

3. Решить следующие системы уравнений:

а)

.

Решение: а). Расширенная матрица системы имеет вид:

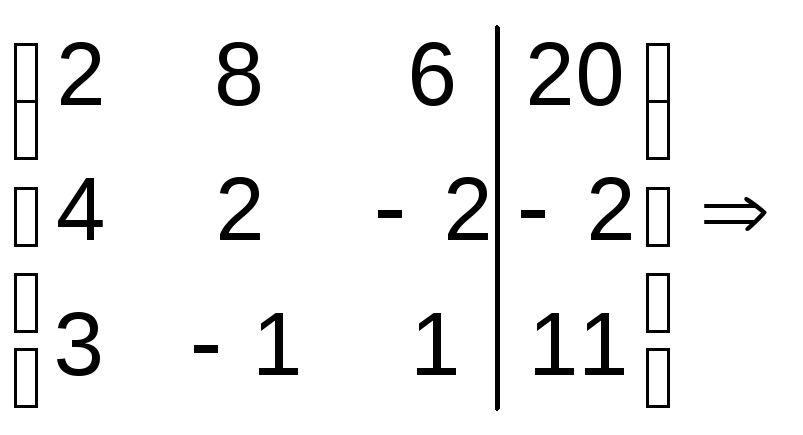Шаг 1. Так как , то разделим первую строку на вторую, получим:

.

Умножая первую стоку матрицы на числа (-4), (-3) и прибавляя полученные строки соответственно ко второй и третьей строке, исключим переменную х₁ из всех строк, начиная со второй, получим:

.

Шаг 2. Так как = -14  0, то разделим 2-ю и 3-ю строки соответственно на (–14) и на (–1)

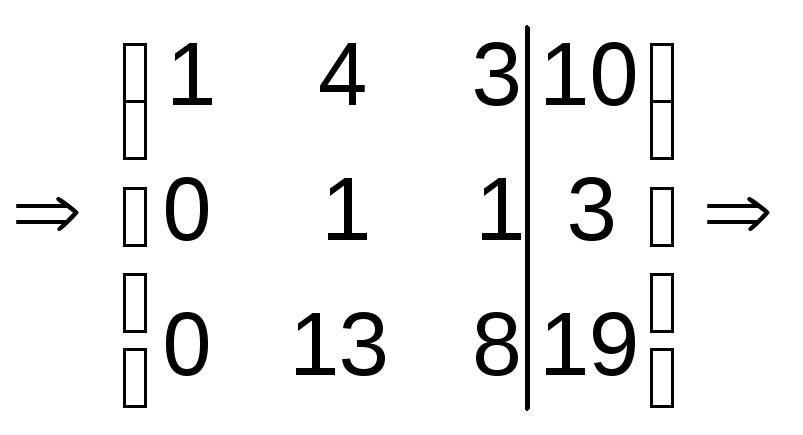
Умножая 2-ю строку на (-13), прибавим к третьей.

.

Используя обратный ход метода Гаусса, найдём

.

Откуда

x₃ = (-20)/(-5) = 4; x₂ = 3 - x₃ = - 1; x₁ = 10 - 4x₂ - 3x₃ = 2,

т.е. наёдено решение системы (2,-1,4)

б) Здесь = 1, расширенная матрица имеет вид

Шаг 1. Умножим 1-ю строку на (-2) и (-4) и прибавим ко второй

и третьей соответственно, получим

Шаг 2. Умножим вторую строку на (-1) и прибавим к третьей

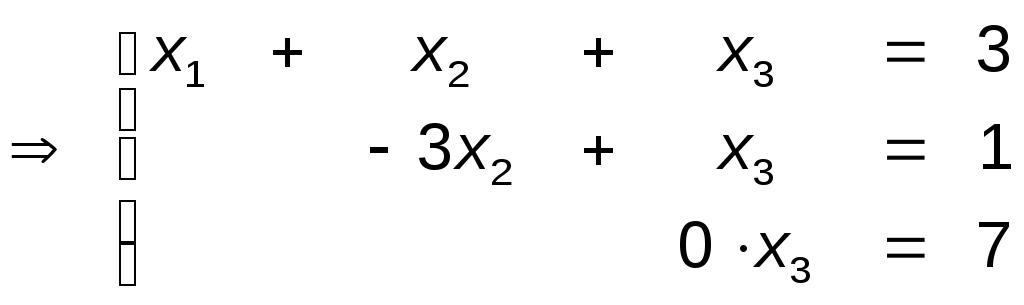
Ясно, что эта система уравнений несовместна и не имеет решения.

в)

Поступая, как и в предыдущих случаях, получим

.

Исходная система сводится к следующей системе:

.

Существует бесконечное число решений, причём все они удовлетворяют соотношениям полагая , получим (()/3, (c-1)/3, c), где с может принимать любое значение.

Для совместных систем линейных уранений верны следующие теоремы:

1. Если ранг матрицы совместной системы равен числу переменных, т.е. r = rangA = n, то система (2) имеет единственное решение.

2. Если ранг матрицы совместной системы меньше числа переменных, т.е. r = rangA < n, то система 2 неопределена и имеет бесконечное множество решений.

Результаты исследования системы (1) приведём в виде следующей схемы (см. стр. 43).

Пусть rang(A) = rangA = r, т.е. система совместна. Не ограничивая общности, будем считать, что базисный минор располагается в первых r (1  r  min (m,n)) строках и столбцах матрицы А. Отбросив последние m - r уравнений системы (1), запишем укороченную систему:

, (5)

которая эквивалентна исходной. Назовем неизвестные базисными, а свободными и перенесем слагаемые, содержащие свободные неизвестные, в первую часть уравнения (5). Получаем систему относительно базисных неизвестных:

a₁₁x₁+...+a_1rx_r= b₁-a₁, _r+1 x_r+1- ... -a_1nx_n,

которая для каждого набора значений свободных неизвестных

b₁,...b_n, имеет единственное решение (X₁,...,X_n), находимое по правилу Крамера. Соответствующее решение укороченной, а следовательно, и исходной систем имеет вид:

(6)

Формула (6), выражающая произвольное решение системы в виде вектор-функции от n - r свободных неизвестных, называется общим решением системы (1).

Схема исследования системы неоднородных линейных алгебраических уравнений

Rang < n

Система неопределённая (бесконечно много решений).

Rang A 

Система несовместная.

Rang < m

Уравнения системы зависимые.

Система m линейных уравнений с n переменными.

Rang = n

Система определённая (единственное решение).

Rang = m

Уравнения системы не зависимые.

Rang A =

Система совместная.

Алгоритм (правило) для решения системы линейных уравнений.

1). Путём вычисления ранга матрицы системы и расширенной матрицы выясняют вопрос о совместности системы; если система совместна, то находят один из гланых миноров M порядка r, равного рангу обеих матриц.

2). Берут r уравнений, в которых лежит минор M; остальные уравнения отбрасывают; r неизвестные коэффициенты, которые входят в главный минор M, обьявляют базисными и оставляют слева, а остальные n-r неизвестные обьявляют свободными и переносят в правую часть.

3). По правилу Крамера находят выражения базисных неизвестных через свободные переменные. Полученные равенства называют общим решением.

4). Придавая свободным неизвестным любые числовые значения, из общего решения находят соответствующие значения базисных неизвестных и тем самым находят решение исходной системы уравнений, которое в отличие от общего решения можно назвать частным решением. Указанным путём можно получить любое решение. Для этого свободным неизвестным в общем решении надо придать те значения, которые они имеют в данном решении.

ПРИМЕР 4. Установить совместность и найти общее решение системы.

.

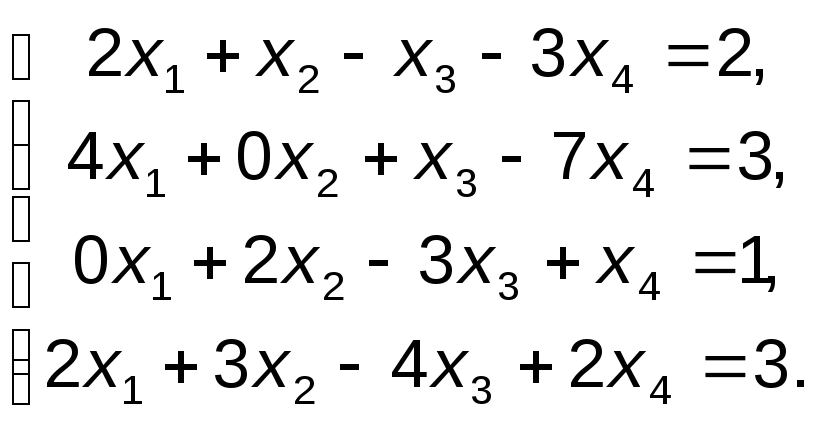РЕШЕНИЕ: Выпишем основную и расширенную матрицу системы:

.

Так как, А = rangA (проверьте!), то исходная система совместна (так как rangA = 2 < 4, то система имеет бесконечно много решений).

Выберем в качестве базисного минора:

.

Тогда неизвестные x, x - базисные, x, x - свободные, а укороченная система имеет вид:

.

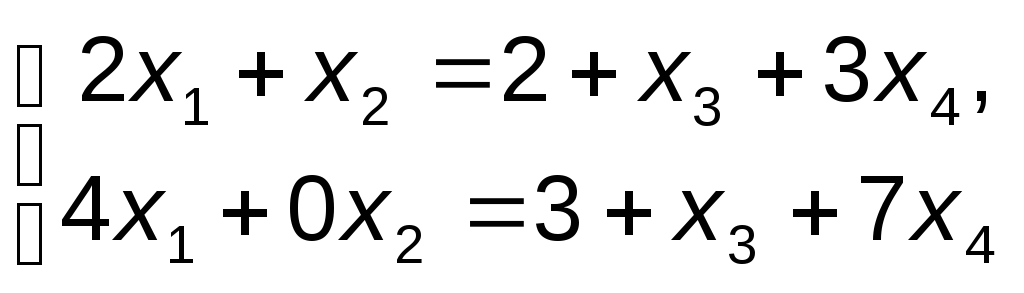Полагая x= с, x= с, и решая укороченную систему относительно базисных неизвестных, получаем

Следовательно, общее решение исходной системы иммет вид:

.

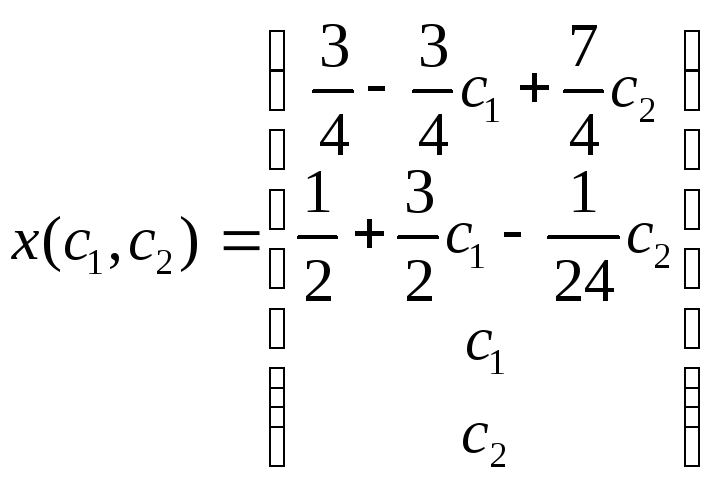Однородная система АХ = 0. Всегда совместна, так как имеет тривиальное решение Х = 0. Для существования нетривиального решения однородной системы необходимо и достаточно, чтобы

r = rangA < n (при m = n это условие означает, что detA = 0).

Пусть Q  Rⁿ множество всех решений однородной системы. Всякий базис во множестве Q состоит из n - r векторов. Соответствующая ему в каноническом базисе система вектор-столбец

( Х₁…Х_n)^Т - называем фундаментальной системой решений. Общее решение однородной системы имеет вид: X =(c₁,...,с_n), где c₁,...,с_n

– произвольные постоянные.

Базисные решения могут быть получены методом, изложенным в предыдущем пункте, если свободным неизвестным придавать поочередно значение 1, полагая остальные равные 0.

Алгоритм (правило) для построения фундаментальной системы решений.

Берут любой определитель D порядка n - r, отличный от нуля (например, определитель, у которого элементы главной диагонали равны единице, а остальные нулю). Свободным неизвестным придают поочередно значения, равные элементам первой, второй и т.д. строк определителя D, и каждый раз из общего решения находят соответствующие значения главных неизвестных. Полученные n - r решений составляют фундаментальную систему. Меняя произвольно исходный определитель D, можно получить различные фундаментальные системы решений.

ПРИМЕР 5. Найти фундаментальную систему решений и общее решение следующей однородной системы уравнений:

РЕШЕНИЕ: Матрица коэффициентов:

имеет ранг r = 2 (проверте!).

Выберем в качестве базисного минора:

Тогда укороченная система имеет вид: 3x₁ + x₂ = 8x₃ - 2x₄ - x₅,

Откуда находим.

Общее решение системы:

.

Из общего решения находим фундаментальную систему решений:

.

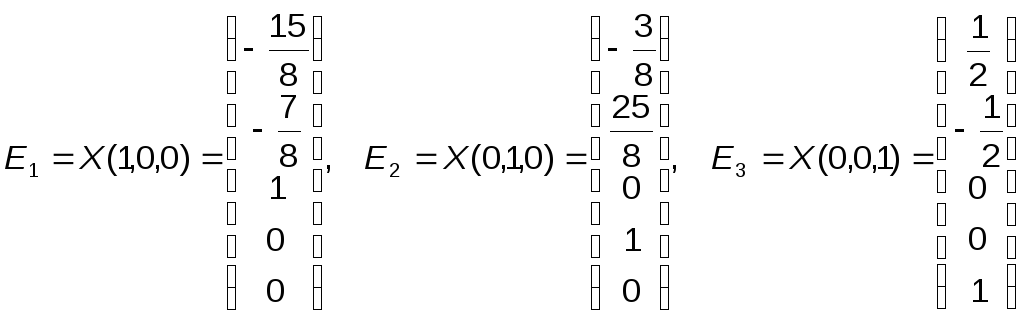С использованием фундаментальной системы общее решение может быть записано в виде:

.

ЗАМЕЧАНИЕ: Если ранг системы однородных линейных уравнений на единицу меньше числа неизвестных: r = n - 1, то n - r = 1 т.е. фундаментальная система состоит из одного решения и любое ненулевое решение образует фундаментальную систему. В этом случае любые два решения различаются между собой лишь числовым множителем.

ПРИМЕР 6. Найти общее решение и фундаментальную систему решений системы уравнений:

РЕШЕНИЕ: Составим матрицу системы

поэтому

Так как это решение не нулевое, то оно образует фундаментальную систему решений. Все решения ему пропорциональны. Значит, общее решение имеет вид:

где с параметр принимающий любые числовые значения. С использованием фундаментальной системы, общее решение может быть записано в виде:

Если в неоднородной системе линейных уравнений заменить все свободные члены нулями, то получится однородная система, называемая приведённой системой для исходной неоднородной системы. Решение даннорй системы и ситемы соответствующей ей приведённой системы связаны следующим образом.

1. Сумма любого решения неоднородной системы и любого решения её приведённой системы является решением неоднородной системы.

2. Разность двух любых решений неоднородной системы является

решением её приведённой системы. Из этих двух свойств следует:Все решения неоднородной системы можно получить, прибавляя к одному (любому) её решению поочередно все решения её приведённой системы. Иными словами, общее решение неоднородной системы можно получить, если к любому частному решению этой системы прибавить общее решение её приведённой системы.

Найти общее решение системы уравнений

.

РЕШЕНИЕ:

Эта система имеет частное решение x = y = z = 1.

Общее решение её приведённой системы найдено в предыдущем примере и имеет вид:

X = 2,

где параметр, принимающий любые значения. Поэтому общее решение данной неоднородной системы уравнений имеет вид x = 1 + 2, где произвольный параметр.

.