Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математический анализ II Курс Лекций

.pdf

Скачиваний:

112

Добавлен:

14.04.2015

Размер:

2.46 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 167 8 9 10 11 12 13 14 15 16 > Следующая >>>

60		Глава 6. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
0	0	a	a
Z	f (x) dx = Z	f ( t) dt = Z	f ( t) dt = Z	f (x) dx:
a	a	0	0

(Воспользовались формулой замены переменной, правилом изменения порядка пределов интегрирования, определением нечетной функции и тем фактом, что величина интеграла не зависит от обозначения переменной интегрирования.)

a	a	a
Окончательно получим Z	f (x) dx = Z	f (x) dx + Z	f (x) dx = 0. J
a	0	0

Свойство 2. Интеграл от четной функции по симметричному относительно нуля промежутку равен удвоенному интегралу по половине про-

							a		a
межутка, т.е., если f (x) четная функция, то Z								f (x) dx = 2 Z		f (x) dx.
							a		0
I Это свойство доказывается аналогично с учетом четности функции:
a		0		a		0		a
Z	f (x) dx = Z		f (x) dx + Z		f (x) dx = Z		f ( x) dx + Z		f (x) dx =
a		a		0	a	a	a	0	a
					= Z0	f (x) dx + Z0		f (x) dx = 2 Z0		f (x) dx:
J		3. Если		f (x) периодическая			функция с периодом T , то
Свойство		3. Если		f (x) периодическая			функция с периодом T , то
a+T		T

	f (x) dx =	f (x) dx, т.е. интеграл по промежутку длиной в период
a	0
не зависит от начала промежутка.
I Разложим интеграл на сумму трех слагаемых:
	a+T	0	T		a+T
	Z	f (x) dx = Z	f (x) dx + Z	f (x) dx +	Z	f (x) dx:
	a	a	0		T

В последнем слагаемом сделаем замену переменной: x = t + T . Тогда

a+T	a	a
Z	f (x) dx = Z	f (t + T ) dt = Z	f (x) dx. (Воспользовались формулой заме-
T	0	0

ны переменной, определением периодической функции и тем, что интеграл

§10. Некоторые формулы, связанные с определенным интегралом

не зависит от обозначения переменной интегрирования.) Тогда

a+T	0		T		a+T
Z	f (x) dx = Z	f (x) dx + Z		f (x) dx + Z		f (x) dx =
a	a		0		T
		T		0		a		T
		= Z0	f (x) dx + Za		f (x) dx + Z0		f (x) dx =	Z0	f (x) dx:

Упражнение. Проиллюстрируйте свойства 1–3 на графиках.

§10 Некоторые формулы, связанные с определенным интегралом

10.1 Вычисление интегралов

cosn xdx и

sinn xdx

Вычислим интегралы In(1) = Z0

cosn xdx и In(2) = Z0

sinn xdx.

I Заметим, что I1(1) = Z0

cos xdx = 1 и I0(1) = Z0

dx =

Вычислим интегралы при n > 2. Сначала в интеграле Z

cosn xdx сделаем

замену переменной x =

t. Тогда

cosn xdx = Z

cosn

dt = Z

sinn tdt:

Следовательно, данные интегралы равны и можно вычислить только один из них.

Возьмем In(1) и преобразуем сначала подынтегральную функцию:

=2		=2			=2
In(1) = Z	cosn xdx =	Z	cosn 2 x	1 sin2 x	dx = In(1)2 Z	cosn 2 x sin2 xdx:
0		0			0

62 Глава 6. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

Второй интеграл в последнем равенстве проинтегрируем по частям,

полагая

u = sin x,

cosn 2 x

sin xdx.

Тогда

cos xdx и

v = Z

n 1

cosn 2 x sin xdx =

cos

, откуда

cosn

1 x

I(1)

cosn 2 x sin2 xdx =

sin x 0

cosn xdx =

n 1

(1)

In(1)

Отсюда In(1) = In 2

. Решая это равенство относительно In(1), по-

n 1

лучим рекуррентную формулу In(1) =

In(1)2.

Тогда для четного n получим

I(1)

n 1

n 3

(1)

n 1

n 3

: : :

(1)

;

n 4

n 2

а для нечетного

I(1)

n 1

n 3

(1)

n 1

n 3

: : :

(1)

n 4

n 2

Учитывая значения I(1) и I(1), получим окончательный ответ:

(2k 1)!!

;

n = 2k;

;

n = 2k + 1;

cosn xdx =

sinn xdx =

(2k)!!

(2k + 1)!!

где k

2 N

10.2 Формула Валлиса

n 2 N выполняется

Пусть 0 < x <

. Тогда

для

любого

неравенство

sin2n+1 x < sin2n x < sin2n 1 x.

Интегрируя

это

неравенство по

промежутку

[0; =2] и используя результат предыдущего пункта, получим неравенство

(2n)!!

(2n 1)!!

(2n 2)!!

(2n + 1)!!

(2n)!!

(2n 1)!!

или

(2n 1)!!

2n + 1 <

(2n 1)!!

2n:

(2n)!!

§10. Некоторые формулы, связанные с определенным интегралом

Тогда будут верны оценки

0 < 2 (2n 1)!!

2n + 1 <

(2n 1)!!

2n + 1

(2n)!!

0 < (2n 1)!!

< (2n 1)!!

(2n 1)!!

2n + 1:

(2n)!!

Так как справедливо неравенство

(2n)!!

;

(2n 1)!!

2n + 1

(2n 1)!!

2n (2n + 1)

n!1

(2n 1)!!

2n = n!1 (2n 1)!!

2n + 1 =

то

lim

(2n)!!

lim

(2n)!!

Равенство

n!1 (2n 1)!!

2n + 1

= 2

lim

(2n)!!

называется формулой Валлиса. Оно является одним из первых представлений числа в виде бесконечного произведения и позволяет достаточно быстро вычислить число с любой заданной точностью.

10.3 Интегральная форма остаточного члена формулы Тейлора

Пусть функция f (t) на промежутке [a; x] непрерывно дифференцируема n + 1 раз. Тогда будет иметь место формула:

f (x) = f (a) +

f0 (a)

(x a) +

f00 (a)

(x a)

+ +

f(n) (a)

(x a)

+ n1! Z f(n+1) (t) (x t)n dt:

Эта формула является уже известной нам формулой Тейлора, где оста-

точный член представлен в виде Rn =		1	Za	f(n+1) (t) (x t)n dt.

		n!
x
I Применим к интегралу Za	f(n+1) (t) (x t)n dt формулу интегрирования по

частям, полагая u = (x t)n, dv = f(n+1) (t) dt. Тогда du = n (x t)n 1 dt,

64	Глава 6. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

v = f(n) (t). Получим

Rn = n1! Z f(n+1) (t) (x t)n dt =

= n1!

0f(n) (t) (x t)n a					x	f(n) (t) (x t)n 1 dt1 =
0f(n) (t) (x t)n a					+ n Z	f(n) (t) (x t)n 1 dt1 =
				x
					a
@											A
@	f	(n)						1		x	A
=	f	(a)	(x a)n +					1		Z	f(n) (t) (x t)n 1 dt:
=		n!	(x a)n +				(n		1)!	Z	f(n) (t) (x t)n 1 dt:

Продолжая интегрирование по частям еще n 1 раз, получим

Rn =

n!(

) (x a)n

1)!

(x a)n 2

01!

f0 (t) dt =

(x a)+Z

f(n) a

f(n 1)

(a)

f (a)

f(n) (a)

f(n 1) (a)

(x a)n 2

f0 (a)

(x a)n

(x a) f (a) + f (x);

1)!

что и доказывает требуемое равенство. J

10.4Формула Стирлинга

Взаключение этого параграфа выведем асимптотическую формулу, из-

вестную под названием формулы Стирлинга.

Рассмотрим последовательность an =

nn+1=2e n

n+1=2

Составим отношение

1 +

. Тогда

an+1

ln an+1 =

n + 2 ln

1 + n

Так как функция y = 1=x монотонно убывает и выпукла вниз при x > 0, то площадь криволинейной трапеции ABCD, ограниченной кривой y = 1=x, осью OX и прямыми x = n и x = n + 1, меньше площади трапеции ABCD и больше площади трапеции AB0C0D, где B0C0 — касатель-

ная к кривой y = 1=x в точке x = n + 12

§10. Некоторые формулы, связанные с определенным интегралом

(см. рис.), что записывается в виде нера-

венства:

n + 1=2

n+1

= ln 1 + n <

n + n + 1

< Zn

Умножим это неравенство на n +

n + 1

( +

1 < n +

ln 1 +

n n

и из каждой его части вычтем 1. Получим

n + 1

( +

4 ( + 1)

0 < n +

ln 1 +

1 <

1 =

n n

или

0 < ln

an+1

4n (n + 1)

Отсюда следует, что an > 1, т.е. последовательность положительных

an+1

чисел an убывающая и ограниченная снизу, следовательно, она имеет предел.

Обозначим lim an = .

n!1

Подставляя в последнее неравенство n + 1; n + 2; : : : n + k вместо n и складывая полученные неравенства, получим

+ +

0 < ln

an+k

4n (n + 1)

4 (n + 1) (n + 2)

4 (n + k 1) (n + k)

= 4

n + k

или 1 <

< e41 (n1

n+k

an+k

< e1=(4n), откуда сле-

Переходя к пределу при k ! 1, получим 1 <

дует, что > 0 и выполняется неравенство < an < e1=(4n), что означает, что

an = e =(4n);

0 < < 1:

(*)

Далее из формулы Валлиса получаем:

(2n)!!

((2n)!!)2

22n+1=2

(n!)2

= nlim

;

2n + 1 (2n)!

2n + 1 (2n 1)!!

!1 2n + 1 (2n)!

66	Глава 6. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

с другой стороны

(an)2

a2n


		(n!)2	(2n)2n+1=2 e 2n		p		(n!)2 22n+1=2
						2
=				=	p				(2n)!	:
	n2n+1e 2n		(2n)!
								2n

(an)2

Следовательно, p = nlim

= p

и =

2 .

!1 a2n

Подставляя

найденное значение

в (*), получим an = p

e =(4n),

2 n

< <

, откуда n

nn+1=2e np

e =(4n) или

! =

n! = p2 n

e =(4n); 0 < < 1:

Последнее равенство называется формулой Стирлинга и позволяет оценивать или приближенно вычислять значения n! при больших n.

Замечание 1. Можно доказать более точную формулу

	n	n
n! = p2 n
		e =(12n); 0 < < 1:
	e

Замечание 2. Формулу Стирлинга часто применяют в асимптотическом

виде:

n! p2 n

при n ! 1:

Пример 1. Исследовать ряд 1

на сходимость.

n=0

, Применим для исследования второй признак сравнения. Пусть an =

nen

bn =

nn2p

. Из формулы Стирлинга следует, что an bn,

2 n

следовательно, если ряд

bn сходится, то данный ряд тоже сходится.

n=1

Очевидно, что если n > 4e, то 0 < bn <

. Отсюда по первому

признаку сравнения ряд

bn сходится. Таким образом, ряд

сходится.

n=1

n=0

Глава 7

ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА

§1 Понятие об измерении множеств в Rn

1.1Определения

1.Пусть fXkgnk=1 — набор множеств произвольной природы. Множество, элементом которого будет упорядоченный набор (x1; x2; : : : xn),

где xk 2 Xk, будем называть декартовым произведением множеств

X1; X2; : : : Xn и обозначать X1 X2 X3 : : : Xn.

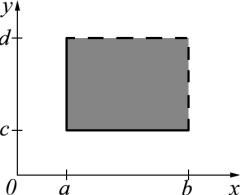
Пример 1. Пусть X = [a; b] и Y = [c; d] — отрезки числовой оси. Тогда X Y = f(x; y) j x 2 X; y 2 Y g — прямоугольник на декартовой плоскости.

2. Декартово произведение A = [a1; b1) [a2; b2) [an; bn), где каждое множество [ak; bk) — полуинтервал вещественной оси, будем называть n-мерной клеткой.

Например, множество плоскости A = f(x; y) j x 2 [a; b) ; y 2 [c; d)g — двумерная клетка, представляет из себя прямоугольник, половина границы которого принадлежит этому прямоугольнику, а половина не принадлежит (см.рис.).

В общем случае n-мерная клетка является множеством пространства Rn.

3. Мерой клетки A будем называть число

(A) = (bk ak).

k=1

Меру двумерной клетки называют также площадью, меру трехмерной клетки — объемом.

Например, площадью двумерной клетки A будет число

(A) = (b a) (d c) :

68	Глава 7. ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА

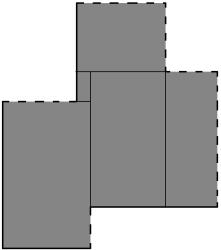
4. Множество E будем называть элементарным, если его можно представить в виде объ-

единения конечного числа непересекающихся

[

клеток E = Ak (см. рис.).

k=1

5.Пустое множество будем считать элементарным.

6.Мерой элементарного множества будем

называть число (E) = (Ak).

k=1

Мера пустого множества равна нулю.

Множество элементарных множеств и мера, определенная на нем, обладают следующими свойствами:

Свойство 1. Если множества E1 и E2 — элементарные, то множества E1 [ E2, E1 \ E2 и E1 n E2 тоже элементарные. Другими словами, множество элементарных множеств образуют алгебру.

Свойство 2. Если множество E можно представить в виде объедине-

ния конечного числа непересекающихся элементарных множеств En, то

(E) = (Ek) (аддитивность меры).

k=1

Свойство 3. Если E1 и E2 — элементарные множества и E1 E2, то(E1) 6 (E2) (монотонность меры).

Свойство 4. Если E1 и E2 — элементарные множества, то имеет место равенство

(E1 [ E2) + (E1 \ E2) = (E1) + (E2) :

Первые три свойства очевидны, поэтому докажем только четвертое.

I Представим множества E1, E2 и E1 [ E2 в виде объединений непересекающихся множеств:

E1 = (E1 n E2) [ (E1 \ E2) ; E2 = (E2 n E1) [ (E1 \ E2) ;

E1 [ E2 = (E1 n E2) [ (E2 n E1) [ (E1 \ E2) :

Тогда по свойству аддитивности меры получим

(E1) = (E1 n E2) + (E1 \ E2) ;

(E2) = (E2 n E1) + (E1 \ E2) ;

(E1 [ E2) = (E1 n E2) + (E2 n E1) + (E1 \ E2) ;

откуда следует требуемое. J

§1. Понятие об измерении множеств в RN

Определение 7.1.1. Пусть — некоторое множество в пространстве

Rn. Число ( ) = sup (E), где супремум берется по всевозможным эле-

ментарным множествам, входящим в , будем называть нижней мерой

множества . Соответственно, число ( ) = inf (E), где инфимум

берется по всевозможным элементарным множествам, содержащим , будем называть верхней мерой множества .

Очевидно, если множество ограничено,

то ( ) и ( ) конечны и выполняется

неравенство ( ) 6 ( ).

Если при этом ( ) = ( ) = ( ), то

будем говорить, что множество измеримо, а

число ( ) называть его мерой.

Мера, введенная таким образом, называет-

ся мерой Жордана.

Пример

Замыкание

n-мерной

клетки

] [a2; b2] [an; bn] — измери-

A = [a1; b1

мое множество и его мера равна

= (A) = (bk ak).

Рассмотрим

последовательность

n-мерных

клеток

Ak = a1; b1 + k an; bn

+ k . Тогда A A Ak.

Отсюда (A) 6

A 6 (Ak). Так как lim (Ak) = (A), то

множество A измеримо и A = (A). -

Пример

Множество

внутренних

точек

-мерной

клетки

int A = (a1; b1) (a2; b2) (an; bn) — измеримое множество и его мера

	kY
равна (int A) = (A) =	(bk ak).

Пример 4. Замыкание и множество внутренних точек int элементарного


множества — измеримые множества и = (int ) = ( ).
Доказательство утверждений в	примерах 3 и 4 предоставляем читателю.

1.2 Свойства измеримых множеств

Свойство 1. Если множества 1 и 2 измеримы, то множества 1 [ 2 и1 \ 2 также измеримы и

( 1) + ( 2) = ( 1 [ 2) + ( 1 \ 2) :

<<< < Предыдущая 1 2 3 4 5 67 / 167 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.03.20162.39 Mб40Математика типовик 3 модуль.pdf
#
23.04.2019514.79 Кб26математика ч.2.docx
#
01.05.20251.14 Mб0математика экзамен.docx
#
20.03.20162.47 Mб26Математика, Типовик 1 семестр 2 модуль.doc
#
14.07.2019246.56 Кб4Математика. Экзамен 2 курс 1 семестр.rtf
#
14.04.20152.46 Mб112Математический анализ II Курс Лекций.pdf
#
14.04.20157.4 Mб96Математический анализ II Учебное Пособие.pdf
#
21.03.2016133.76 Кб39Математический язык.docx
#
01.04.2025244.22 Кб0Материалы к контрольной 1.Древнегреческая филос...doc
#
25.11.2019854.35 Кб36Материалы лекций_ЭКиТ_текущие_В.Скобелев_1.docx
#
21.03.2016596.2 Кб8Материалы тест №2.pdf