Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математический анализ II Курс Лекций

.pdf

Скачиваний:

Добавлен:

14.04.2015

Размер:

2.46 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

100 Глава 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ПЕРВОГО И ВТОРОГО РОДА

Пример 4. Исследовать на абсолютную и условную сходимость интегралы:

1 cos kx

arcsin (1

x) cos 1

x ln x

dx, k > 0; b)

dx;

cosp

dx;

x5=3

d) Z

+ x

ln x

dx; f) Z

sin xdx

sin

; e)

sin

sin x

x (1

x2)3=2

, a)

Очевидно,

что при s > 1

интеграл сходится

абсолютно, так как

(kx)	1			Z	dx
cos	6		, а интеграл			сходится.
xs	6	xs	, а интеграл		xs	сходится.
				1

Если s < 0, то интеграл расходится по признаку Коши. Действительно,

возьмем 1 =

2 n

и 2

(2n + 1) +

. Тогда

k (2n+1)+

cos (kx)

k (2n+1)+

cos (kx) dx

2 n

2 nZ

2 n

Так как последняя величина стремится к бесконечности при n ! 1,

то в качестве "0 можно взять произвольное положительное число, чтобы утверждать, что, какую бы окрестность бесконечности мы ни взяли, всегда найдутся такие значения 1 и 2, что будет выполняться неравенство

2	cos (kx)dx	> "0.
Z

1
При s = 0 непосредственным интегрированием убеждаемся, что интеграл
расходится.
Наконец рассмотрим случай, когда 0 < s 6 1. С помощью признака

Дирихле докажем, что интеграл сходится условно. Положим g (x) = cos (kx)

и f (x) =

. Тогда

x cos (kx) dx

sin (kx) sin k

6 jsin (kx)j + jsin kj 6

x g (t) dt

т.е.

первообразная

от этой функции

ограничена. Функция

f (x) =

убы-

вает на промежутке интегрирования и стремится к нулю. Условия теоремы Дирихле выполнены, и интеграл сходится.

§2. Признаки сходимости несобственных интегралов

101

В этом случае абсолютной сходимости интеграла нет, так как

cosxs

(kx)

cos2 (kx)

1 + cos (2kx)

Интеграл от последней

функции

расходится, так как

1 +

cos (2kx)

dx = Z1

+ Z1

cos (2kx)

dx;

и в последней сумме второй интеграл сходится (условно, по признаку Дирихле), а первый расходится.

arcsin (1

x) cos 1

b) В интеграле Z0

dx особая точка x = 0. Применим

x5=3

cos 1

признак Абеля, положив g (x) =

и f (x) = arcsin (1 x).

x5=3

cos 1

интеграле

сделаем замену переменной t =

. То-

x5=3

cos 1

+1cos t

гда

этот интеграл сходится.

Функция

x5=3

f (x) = arcsin (1 x)

ограничена и монотонна. Следовательно, данный ин-

теграл сходится условно. Абсолютной сходимости здесь нет, так как на промежутке [0; 1=2] выполняется неравенство

x5=3

x >

6 x5=3x

= 6

x5=3

+ x5=3 !:

arcsin (1

x) cos 1

cos2 1

cos

1=2

cos 2

Интеграл

dx сходится

(аналогично

предыдущему), а

интеграл

x5=3

1=2

arcsin (1

x) cos

x5=3

x5=3 расходится. Следовательно, интеграл Z

dx рас-

ходится, и данный интеграл не сходится абсолютно.

c) В интеграле Z

x ln x

cosp

dx две особые точки: x = 0 и x = 1. Поэтому

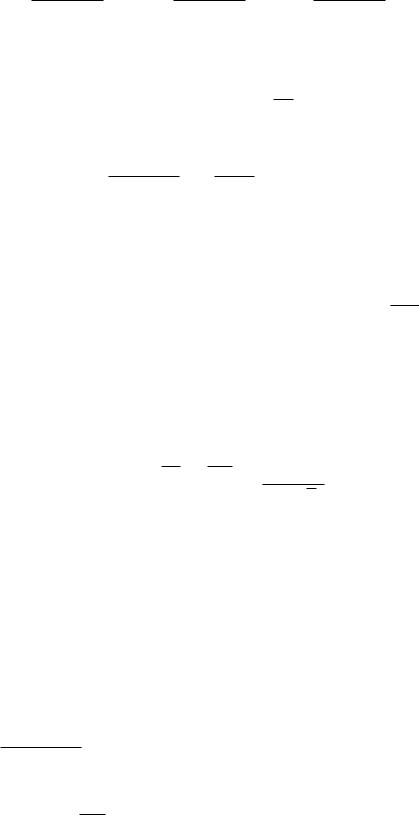
102 Глава 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ПЕРВОГО И ВТОРОГО РОДА

разобьем этот интеграл на сумму двух:

cos x ln x

dx = Z0

x ln x

dx + Z1

cos x ln x

cosp

dx:

Так как lim (x ln x) = 0, > 0, то в некоторой окрестности нуля выпол-

x!0

няется неравенство jx ln xj < 1 или jln xj < x1 . Следовательно, если взять

= 1=4, то в этой окрестности будет выполняться неравенство

ln x

x ln x

cosp

x3=4

Так как Z0

сходится, то первый интеграл сходится абсолютно.

x3=4

ln x

Во втором интеграле положим

g (x) = cos x,

f (x) =

и применим

признак Дирихле. Первообразная от функции g (x): Z1

cos xdx = sin x sin 1

ограничена. Функция f (x) стремится к нулю при x ! +1. Исследуем ее на монотонность с помощью производной:

1				ln x
	p			2p
f0 (x) =	p	x		2p	x
f0 (x) =			x
			x

2 ln x

= 2xpx :

Эта производная будет отрицательной для всех значений x 2 e2; +1 , следовательно, условия теоремы Дирихле выполнены и интеграл сходится условно.

Абсолютной сходимости второго интеграла нет. Действительно, выполнено неравенство

x ln x

cos2 x ln x

ln x

cos 2x ln x

cospx

= px

> px

2x ln x

Интеграл

cosp

сходится (доказывается аналогично доказанному

выше), а интеграл

расходится. Следовательно, расходится интеграл

от суммы, и данный интеграл не сходится абсолютно.

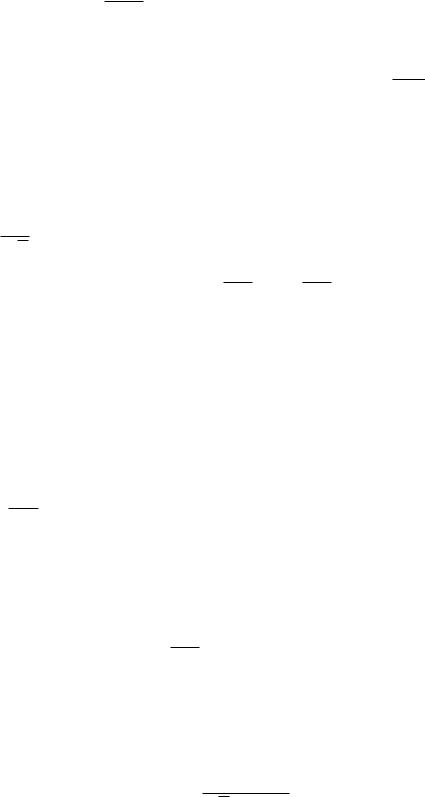
§2. Признаки сходимости несобственных интегралов

103

d) Сделаем замену переменной по формуле t =

1 + x

. Тогда

1 x

t 1

x =

; dx =

2dt

; 1 x2 =

t + 1

(1 + t)

(t + 1)

+ x

sin t (t + 1)

dt = Z

sin t

dt + Z

sin t

sin

dt:

x (1

x2)3=2

t3=2

Аналогично тому, как это было сделано выше, доказывается, что первый интеграл сходится условно, а второй абсолютно. Следовательно, данный интеграл сходится условно.

e) Особой точкой является точка x = 1. Очевидно, выполняется условие

ln x

lim p = 0, поэтому для подынтегральной функции справедлива форму-

x!+1 x

ла Тейлора – Маклорена:

ln x

+ R (x). Используя известное

sin

неравенство t > sin t > t

, t > 0, оценим остаток

jR (x)j =

ln x

sin px

< 3!

Так как для

достаточно

больших

значений

x справедливо неравенство

ln x < x1=12,

то

для

этих

же значений x будет справедливо неравенство

ln x

+1 dx

0 <

. Интеграл

сходится, следовательно, интеграл

x5=4

R (x) dx сходится абсолютно, и поведение данного интеграла совпадает с

ln x

поведением интеграла

dx (теорема 8.2.7). Последний интеграл расхо-

дится, следовательно, данный тоже расходится.

f) Этот пример доказывает, что условие монотонности функции f (x) в теореме Дирихле существенно и не может быть отброшено.

Если к этому интегралу попытаться применить признак Дирихле, поло-

жив g (x) = sin x и	1	, то будут справедливы только два
	f (x) = px sin x

условия теоремы: ограниченность первообразной от g (x) и стремление к нулю функции f (x). Однако будет нарушена монотонность этой функции.

104 Глава 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ПЕРВОГО И

ВТОРОГО РОДА

Докажем, что интеграл расходится. Преобразуем подынтегральную функцию

sin x

sin2 x

sin3 x

sin x

+ o

x3=2

sin3 x

+1sin3 x

Тогда

сходятся

абсолютно,

интеграл

x3=2

+1sin x

+1sin2 x

сходится

условно,

интеграл

dx расходится,

следова-

тельно, данный интеграл расходится. -

Глава 9

ЧИСЛОВЫЕ РЯДЫ

§1 Ряды с положительными членами

Понятие о числовом ряде было введено в § 5 главы II. Здесь мы изучим эту тему подробнее.

Рассмотрим сначала числовой ряд

an; где an > 0; n 2 N:

(*)

n=1

Как мы уже знаем, такие ряды можно исследовать на сходимость с помощью признаков сравнения (п. 5.2 главы II). Рассмотрим еще несколько признаков сходимости этих рядов.

Теорема 9.1.1 (Признак Даламбера). Пусть дан ряд

an, где an > 0.

Тогда

n=1

an+1

a) Если

< 1, то ряд сходится;

lim

б) Если

n!1 aan+1n

> 1, то ряд расходится.

lim

n!1

I a) Пусть

an+1

= ` < 1. Возьмем " =

1 `

. По свойству верхнего

lim

n!1

предела (теорема 2.4.3) существует такой номер n0, что для всех n > n0

выполняется неравенство	an+1	< ` + " =	1 + `		. Обозначим =	1 + `		< 1.
	an			2			2

Тогда для всех n > n0 будут выполняться неравенства an+1 < an, т.е.

an0+1 < an0 ;

an0+2 < an0+1 < 2an0 ;

: : :

an0+k < kan0 :

105

106	Глава 9. ЧИСЛОВЫЕ РЯДЫ
1
Так как ряд Xan0 k	сходится (как геометрическая прогрессия), то по

k=1

признаку сравнения (2.5.7) данный ряд тоже сходится.

б) Пусть lim	an+1	= ` > 1. Возьмем " =	` 1	. По свойству нижнего
	an		2
n!1

предела (теорема 2.4.3) существует такой номер n0, что для всех n > n0

выполняется неравенство	an+1	> ` " =	1 + `	> 1.
	an		2

Следовательно, для указанных значений n последовательность fang

возрастает. Тогда для		этих		же значений n выполняется неравенство
an > an0 6= 0, откуда следует, что an 9 0,					следовательно, ряд расходится.
J			an+1	> 1 > lim	an+1
Замечание 1. Если	lim					, то вопрос о сходимости
			an
n!1				n!1	an

ряда остается открытым (т.е. можно найти как сходящиеся, так и расходящиеся ряды, для которых выполняется данное условие).

Приведем примеры таких рядов.

Пример 1. Рассмотрим ряд 2 + 22

+ 42 +

5 +

+ : : : .

2k + 1 + (2k + 1)2

! : 4k2

nlim

= klim

a2k

= klim

= 1;

an+1

a2k+1

nlim

= klim a2k 1

= klim

4k2

1 +

(2k

1)2

= 0:

an+1

a2k

Этот ряд расходится, так как для его частичной суммы выполняется неравенство

Sn >

[

n2 1

]

[

n2 1

]

2i + 1

+ (2i + 1)2 !

[

n2 1

]

2i + 1;

i=0

a2i+1 = i=0

а правая часть этого неравенства стремится к бесконечности, как частичная сумма ряда, общий член которого эквивалентен общему члену гармонического ряда. -

a X

Пример 2.

Теперь рассмотрим ряд

n=1

n+1

= 1. Но, как известно, данный ряд

, lim

= lim

n!1

сходится. -

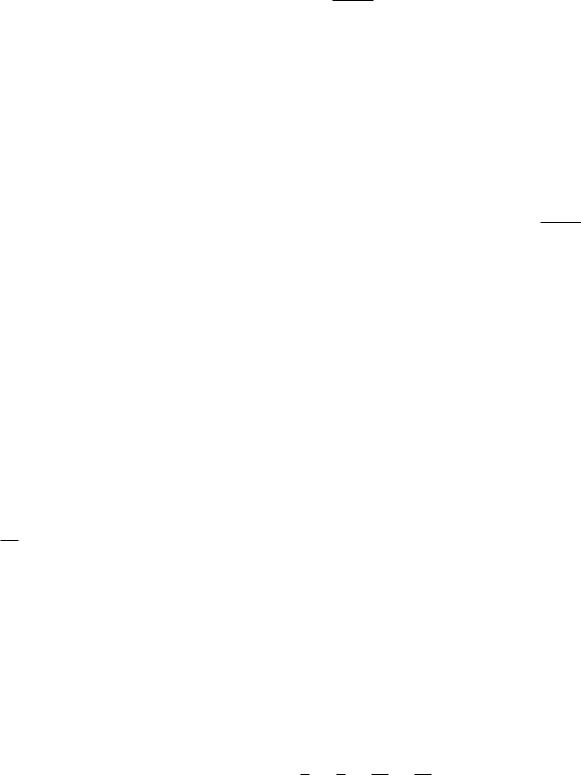
§1. Ряды с положительными членами

107

Теорема 9.1.2 (Радикальный признак Коши). а) Если

< 1, то

lim

ряд (*) сходится;

n!1

б) Если

> 1, то ряд (*) расходится.

lim

n!1

I a) Пусть

= ` < 1. Возьмем " =

1 `

> 0 и найдем номер n0,

lim

n!1

` + 1

начиная с которого будет выполняться неравенство

< ` + " =

< 1.

` + 1

Обозначая

= , получим, что для всех n > n0 выполняется неравен-

ство an < n, т.е. общий член данного ряда не превосходит общего члена

геометрической прогрессии со знаменателем (0 < < 1). Следовательно, по признаку сравнения данный ряд сходится.

б) Пусть теперь

= ` > 1. Это означает, что существует та-

lim

n!1

nig

ni !

кая

подпоследовательность

что npi

`. Тогда, взяв " =

` 1

можно найти

номер

n0,

начиная

с которого

выполняется

неравенство

npi

> `

" =

` + 1

> 1,

т.е. для

всех n

> n

выполняется

неравенство


ani > ni ! +1,		l + 1			. Следовательно, последовательность не стре-
	=
	=		2
мится к нулю и данный ряд расходится. J
Замечание 2. Если			pn		= 1, то вопрос о сходимости ряда остается
		lim
		lim		an
	n!1

открытым (существуют как сходящиеся, так и расходящиеся ряды, для которых выполняется данное условие). Для доказательства достаточно

рассмотреть те же примеры, что и в признаке Даламбера. Легко видеть,

что в обоих случаях будет

= lim

= 1.

lim

n!1

Замечание 3. Если существует

lim

an+1

= ` в

теореме 9.1.1 или

p n!1 an

lim n an = ` в теореме 9.1.2, то ряд сходится, если ` < 1, расходит-

n!1

ся, если ` > 1 и невозможно сделать вывод о сходимости ряда, если ` = 1. Замечание 4. Можно доказать, что признак Коши сильнее признака Даламбера в следующем смысле: если признак Даламбера дает сходимость ряда, то признак Коши тоже дает сходимость; если признак Коши не позволяет сделать никаких заключений, то признак Даламбера тоже не позволяет сделать никаких заключений; однако, существуют ряды, сходимость которых можно установить по признаку Коши, но при этом признак Даламбера не позволяет сделать никаких заключений.

1 1 1 1

Пример 3. Исследуем на сходимость ряд 2 + 5 + 22 + 52 + : : : .

, Применим сначала признак Коши.

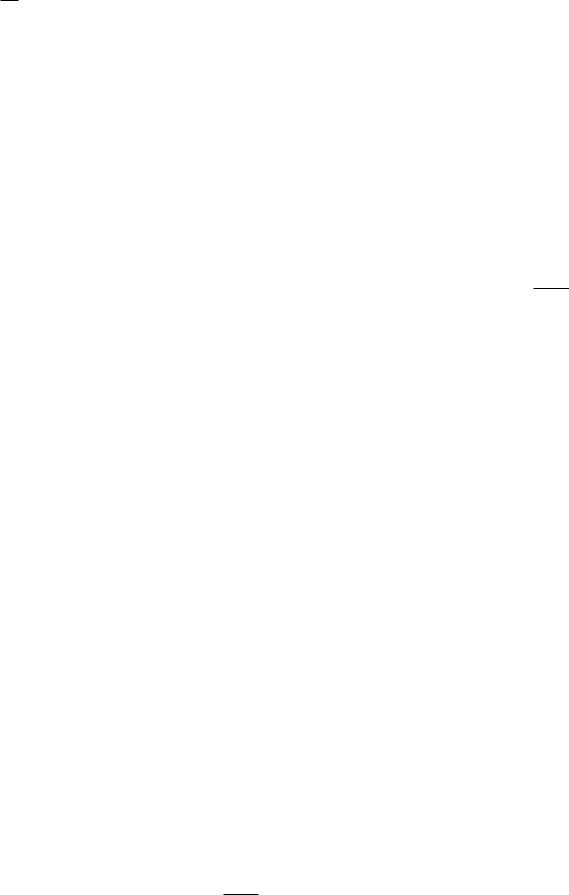
108	Глава 9. ЧИСЛОВЫЕ РЯДЫ

p Рассмотрим две сходящиеся подпоследовательности последовательности f n ang: для n = 2k и для n = 2k 1, k 2 N. (Других сходящихся подпоследовательностей, по существу отличных от двух, указанных выше, нет.) Очевидно,

k!1 p

= k!1 r

= p5

lim

lim 2k

k!1

2k 1 = k!1

= p2

2k 1 1

lim

2k 1

lim

;

тогда lim

и, следовательно, ряд сходится.

Теперь попробуем применить к этому ряду признак Даламбера.

Рассмотрим две подпоследовательности последовательности an+1 : для an

n = 2k и для n = 2k 1. Здесь

	a2k+1			5k			a2k			2k
klim			= nlim		= 1;	klim			= nlim		= 0
klim	a	2k	= nlim	2k+1	= 1;	klim	a	2k 1	= nlim	5k	= 0
!1		2k	!1			!1		2k 1	!1

и признак Даламбера не дает ответа. -

Замечание 5. Из доказательства теорем следует, что если признаки Даламбера или Коши дают расходимость ряда, то общий член ряда не стремится к нулю. Это замечание будет использовано в дальнейшем.

Лемма (4-ый признак сравнения). Пусть даны два ряда

1	1
X	X
an (1) и	bn (2);
n=1	n=1

причем an > 0 и bn > 0, и для всех n (может быть, начиная с некоторого)

выполняется неравенство	an+1	6	bn+1	. Тогда
	an
			bn
a) если ряд (2) сходится, то ряд (1) сходится;
б) если ряд (1) расходится, то ряд (2) расходится.

I Неравенство	an+1	6	bn+1	равносильно неравенству			an+1	6	an	, откуда сле-
	an						bn+1
			bn		an				bn
дует, что последовательность						невозрастающая. Следовательно, она огра-
					bn

ничена сверху, т.е. для всех значений n выполняется неравенство an 6 Cbn. Тогда утверждение леммы следует из первого признака сравнения рядов. J Теперь мы уточним признак Даламбера. Следующие две теоремы приме-

няются в случаях, когда lim an+1 = 1.

n!1 an

§1. Ряды с положительными членами		109
	1
Теорема 9.1.3 (Признак Раабе). Пусть дан ряд	Xan, где an	> 0, и

n=1

nlim n

an+1

= s. Тогда, если s > 1, то ряд сходится, и если s < 1,

то ряд расходится.

I Возьмем " =

s 1

и найдем n0, начиная с которого, выполняется нера-

an+1

s + 1

венство n 1

> s " =

= r > 1. Преобразуя это неравенство,

an+1

сначала получим

< 1

, откуда

> 1 +

. Избавля-

an+1

n r

ясь в последнем неравенстве от знаменателя, получаем nan > nan+1 + ran+1,

откуда nan nan+1 an+1 > ran+1 an+1 или

nan (n + 1) an+1 > (r 1) an+1:

(**)

Так как r > 1, то nan (n + 1) an+1 > 0, откуда следует, что положительная последовательность nan убывающая, следовательно, она имеет предел. Обозначим этот предел через .

Частичная сумма ряда с общим членом bn = nan (n + 1) an+1 будет

равна

(nan (n + 1) an+1) = a1 (m + 1) am+1

n=1

и ряд сходится к a1 . Следовательно, в силу неравенства (**) данный ряд тоже сходится.

n!1	1 an
Докажем вторую часть теоремы. Пусть lim n	an+1	= s, где
Докажем вторую часть теоремы. Пусть lim n		= s, где

s < 1. Тогда, начиная с некоторого номера будет выполняться неравенство

n 1

an+1

< 1. Отсюда

an+1

> 1

n 1

1=n

1=(n 1)

Так как ряд X 1 расходится, то по доказанной выше лемме данный ряд

n=1 n

тоже расходится. J

	1
Теорема 9.1.4 (Признак Гаусса). Пусть дан ряд	Xan, где an > 0, и

n=1

an+1	= +		+ O		1	, где , и — постоянные, причем > 0. Тогда
				n1+
an		n

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.04.2015857.82 Кб10математика +.pdf
#
21.03.20162.39 Mб38Математика типовик 3 модуль.pdf
#
23.04.2019514.79 Кб16математика ч.2.docx
#
20.03.20162.47 Mб24Математика, Типовик 1 семестр 2 модуль.doc
#
14.07.2019246.56 Кб3Математика. Экзамен 2 курс 1 семестр.rtf
#
14.04.20152.46 Mб99Математический анализ II Курс Лекций.pdf
#
14.04.20157.4 Mб87Математический анализ II Учебное Пособие.pdf
#
21.03.2016133.76 Кб36Математический язык.docx
#
25.11.2019854.35 Кб26Материалы лекций_ЭКиТ_текущие_В.Скобелев_1.docx
#
21.03.2016596.2 Кб7Материалы тест №2.pdf
#
20.03.201619.35 Кб32матрица переходных вероятностей.docx