2.1.4. Математическая модель амбивалентных систем с переменными коэффициентами

_{Представляет большой интерес исследование поведение амбивалентной системы, когда параметры системы  и  являются не постоянными, а переменными во времени величинами и более того, связаны с вероятностями состояний системы. Здесь, очевидно, возможны два варианта работы системы: прямо пропорциональная зависимость и обратно пропорциональная.}

_{Рассмотрим вариант работы системы, когда интенсивности перехода пропорциональны вероятностям состояний. Этот случай представляет несомненный практический интерес. Не ограничивая общности рассмотрения, можно при исследовании считать равным единице коэффициент пропорциональности, тогда и система дифференциальных уравнений, описывающая этот случай становится нелинейной:}

_{= P (A), = P(Ā),}

_{P(A)t = - P} ²_{(A)t + P(A)t P(Ā )t ,}

_{P(A Ā)t = P} ²_{(A)t – [ P (A)t + P (Ā)t ] P (A Ā )t + P} ²_(Ā)t

_{P(Ā)t = - P} ²_{(Ā)t + P (A)t P (A Ā )t}

_{P(A)t + P (A Ā )t + P(Ā)t = 1 , P (A)0 = 1}

_{На рис.2.25 показано решение данной нелинейной системы.}

_{Рис. 2.25}

_{Как видно из рисунка такая система также приходит в состояние равновесия, когда P(A)= P(Ā)= P(AĀ)= 0,333, но состояние смеси устанавливается раньше других, причем через точку перегиба: действительно, при t = 1,5 P(AĀ)= 0,35 , а затем уже при t = 7 P(AĀ)=0.333.}

_{Исследуем поведение данной системы на устойчивость. По аналогии с вариантом системы с постоянными коэффициентами, задаём приращение в точке равновесия}

_{С учётом нормировочного условия получаем, что}

_{поэтому достаточно рассмотреть только изменения для и .}

_{Для анализа устойчивости, достаточно линеаризовать полученные уравнения, осуществляя одновременно параллельный перенос}

_{Находим собственные значения матрицы системы для осуществления ортогонального преобразования}

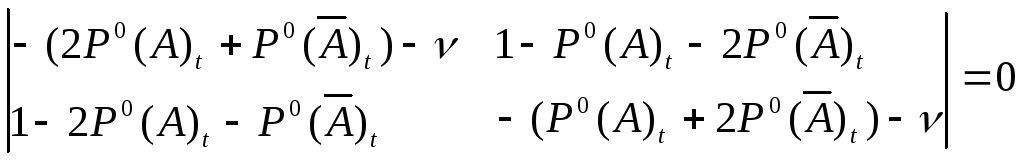
_{Аналогично линейному случаю с учётом поворота оси координат}

_{и система не устойчива, если}

_{Очевидно, что предполагаем, что тогда должно выполниться:}

_или

_,

_{и, согласно нормировочному условию,}

_{Значит положение, при котором}

_{, а}

_{неустойчиво. При}

_{бинарная система устойчива.}

_{Первый вариант исследования поведения данной системы иллюстрирует принцип мирного сосуществования двух противоположностей.}

_{Был проведен анализ второго варианта нелинейной системы с противоположностями, когда интенсивности перехода обратно пропорциональны вероятностям состояний:}

_{= 1/P (A)t , = 1/P(Ā)t ,}

_{P(A)t = -1 + P(AĀ)t /P(Ā)t ,}

_{P(AĀ)t = 2 – (1/P(A)t + 1/P(Ā)t ) P(AĀ)t ,}

_{P(Ā)t = -1 + P(Ā)t / P (A)t ,}

_{P(A)0 = P (A Ā )0 = 0.3 P(Ā)0 = 0.4}

_{На рис. 2.26 показаны результаты решения задачи. Система является неустойчивой и уже при малых значениях времени функционирования ( t  0,5 ) процесс расходится.}

_{Рис. 2.26}

_{Из рис.2.26 видно, что со временем начинает преобладать та противоположность, которая в начальный момент времени имеет большее значение:}

_{при t =0 P(Ā)=0.4, тогда как P(A)= P(AĀ)= 0.333}

_{и уже при t =0,7 P(Ā)=1.}

_{Второй вариант иллюстрирует поведение амбивалентной системы с противоречиями, носящими антагонистический характер, когда одна противоположность существенно подавляет другую.}