Энергия упругой деформации. Упругий гистерезис.

Внешняя сила, перемещая части деформируемого тел а, совершает некоторую работу против внутренних сил, возникающих в теле во время деформации. При исчезновении деформации внутренние силы могут совершать работу против сил внешних. Если тело абсолютно упруго, то работа внешней силы равна работе сил внут­ренних. При деформации абсолютно упругого тела (достаточно мед­ленной, чтобы пренебречь изменением кинетической энергии) потен­циальная энергия его возрастает на величину работы, совершенной внешними силами. В реальных телах часть внутренних сил носит характер сил внутреннего трения. Поэтому работа деформирующей силы частично идет на необратимое увеличение внутренней, а не потенциальной энергии тела. Однако при деформациях, для которых справедлив закон Гука, можно считать, что вся работа внешних сил и для реальных тел идет на увеличение только их потенциальной энергии.

Подсчитаем потенциальную энергию, кото­рую приобретает пружина, растянутая на величину : силой F, пропорциональной удлинению:

где k — коэффициент пропорциональности между силой и вызван­ным ею удлинением .

Так как в пределах применимости закона Гука коэффициент k для данного материала — величина постоянная и не зависит от ве­личины деформации, то можно написанное равенство переписать в виде

(4)

Если закон Гука не выполняется, то и в этом случае элементар­ная работа силы F, вызывающей деформацию , равна:

, (5)

где : — достаточно малая величина деформации, при которой можно считать силу F постоянной в пределах изменения деформации от х до х+Δх,Выделим в деформируемом теле куб, ребро которого равно l. Тогда независимо от вида связи F=F(x) элементарная работа:

Полная работа силы F, вызвавшей деформацию :

(16)

Построим график зависимости относительной деформации от на­пряжения, откладывая по оси ординат величину ±р, по оси абсцисс (рис.6).

Рис.6

Положим, мы сообщили стержню относительное удли­нение , причем изменение напряженияр с изменением происхо­дило по кривойОА. Когда действие внешней силы прекратится и на­пряжения станут равными нулю, то деформация в реальном теле полностью не исчезнет. При р=0 остаточная деформация равна (точка В). Если мы теперь сожмем тело, то деформация исчезнет, когда напряжение в теле приобретет некоторое значение — р₀ (точка С). Это явление называется упругим гистерезисом. Сжимая тело далее, мы достигнем некоторых значений напряжения и отно­сительной деформации, соответствующей точке А'. После прекра­щения действия сжимающей тело силы напряжение становится рав­ным нулю при относительной деформации —(точкаВ'). Теперь деформация тела исчезнет, если в теле возникнет напряжение +р₀ (точка С'). Вновь растягивая тело, мы попадем в точку А. При перио­дически повторяющихся деформациях графическая зависимость р от изображается, таким образом, замкнутой кривой, которая носит названиепетли упругого гистерезиса. Внешние силы, соответствующие участку графика В'С'А , совершают работу, пропорциональную площади, заключенной между кривой В'С'А, ординатой точки А и осью абсцисс. На участке кривой АВ работу совершают внутрен­ние силы. Она пропорциональна площади, заключенной между кри­вой АВ, ординатой точки А и осью абсцисс. Разность этих площадей, равная площади верхней части пет­ли гистерезиса, пропорциональна разности работ внешних и внутрен­них сил. Нижняя часть петли ги­стерезиса также дает разность ра­бот внешних и внутренних сил. Таким образом, площадь петли гистерезиса пропорциональна той части механической энергии, кото­рая за каждый цикл изменения на­пряжения в образце переходит во внутреннюю энергию.

Чем больше петля гистерезиса для данного материала, тем быстрее и сильнее нагревается деталь, выполненная из него, под дейст­вием переменных нагрузок. Поэтому ответственные детали машин, подвергающиеся периодическим нагрузкам (например, пружины клапанов автомобильного или авиационного двигателя), делают из специальных сортов стали, для которых петля гистерезиса мала.

Явление гистерезиса используется для ограничения величины колебаний при вибрациях. Например, для того чтобы в случае ре­зонанса амплитуда колебаний лопаток турбин под действием ударов струи не возрастала до опасной величины, лопатки изготавливаются из материалов с большой петлей гистерезиса (например, хромистые стали). Амплитуда колебаний стабилизируется и перестает расти, как только расход энергии вследствие наличия гистерезиса становит­ся равным ее поступлению.

Большое значение имеет гистерезис в процессе трения. Повто­ряющиеся при трении удары поверхностей тела создают в них перио­дически меняющиеся деформации. Так как во всех реальных телах возникают остаточные деформации (а вместе с тем и упругий гистерезис), то последний и обеспечивает при трении механизм превраще­ния механической энергии во внутреннюю энергию тела.

Лекция№17 Неинерциальные системы отсчета. Силы инерции. Силы инерции в неинерциальной системе отсчета, которая равномерно вращается. Центробежная сила инерции.

Системы отсчета, движущиеся ускоренно относительно одной из инерциальных систем, называются неинерциальными. Они свя­заны с телами отсчета, находящимися во взаимодействии с внешними (по отношению к системе) телами.

Рассмотрим, как различается характер движения тел относительно инерциальной системы и системы неинерциальной, перемещающей прямолинейно и ускоренно относительно первой. Как и в случае инерциальных систем,

(1)

Но теперь — некоторая функция времени.

Дифференцируя по t получим:

(2)

(3)

В этом случае не только скорости тела, но и ускорения его в обеих системах различны:

(4)

Абсолютная скорость равна геометрической сумме относительной и переносной скоростей.

Абсолютное ускорение равно геометрической сумме относительного и переносного ускорений.

Пример. Пусть корабль движется параллельно линии берега с ускорением jЕсли тело покоится на палубе корабля, то относительно берега оно движется с переносной скоростью, равной скорости движения корабля,и, поскольку эта скорость изменяется, обладает переносным ускорением. Если само тело перемещается по палубе со скоростьюи ускорением,то перемещение относительно берега происходит со скоростью и ускорением

Этот результат, полученный для прямолинейного поступательного переносного движения, справедлив для любого поступательного переносного движения, поскольку перемещение в этом случае может быть заменено суммой элементарных прямолинейных пере­мещений.

Составим уравнение движения точки массой mотносительно подвижной системы отсчета . Положим ускорение точки относительно неподвижной системы равным, а действующую силу равной F. Тогда для неподвижной системы в соответствии со вто­рым законом Ньютона

(5)

Второй закон Ньютона в системах отсчета, движу­щихся с ускорением, в число сил, действующих на тело, включает взятое с обратным знаком произведение мас­сы тела на переносное ускорение.

Это произведение, учитывающее ускоренное движение системы отсчета, носит название силы инерции. Для составления уравнений движения тела относительно системы отсчета, движущейся с ус­корением, к результирующей сил, приложенных к телу, надо доба­вить силу инерции.

Рассмотрим несколько конкретных примеров движения тел.

На тележке, покрытой гладким стеклом, лежит шарик. Сооб­щим тележке ускорение (рис. 1). Что произойдет с шариком?

Рис. 1. Шарик на гладкой поверхности движущейся тележки.

В системе координат, связанной с Землей шарик остается в по­кое, ибо на него в направлении движения тележки не действуют ни­какие силы (сила трения мала, и ею можно пренебречь). Относительно тележки шарик перемещается с ускорением

В системе координат, связанной с тележкой, шарик приобретает ускорение, хотя на шарик при этом никакие силы не действуют. Наблюдение за движением шарика позволяет нам сделать заклю­чение, что система отсчета движется с ускорением, и при составле­нии уравнения движения шарика необходимо считать, что на него

действует сила инерции: F=-m, откуда ускорение шарика относительно тележки:

Положим, что в лифте на пружинных весах подвешен груз мас­сой т. На него действуют сила тяжести mg, направленная вниз, и упругая сила R со стороны растянутой пружины, направленная вверх. Так как векторы сил направлены по одной прямой, то, приняв ее за ось координат, мы можем оперировать с модулями ука­занных векторов. Под действием уравновешивающих друг друга сил G=mg и R груз находится в покое.

Если лифт начал двигаться с ускорением , направленным вверх, то точка прикрепления пружины начнет двигаться вверх с тем же ускорением. Вследствие инерции витки пружины и груз движутся вначале с ускорением меньшим, чем ускорение лифта. Поэтому пружина несколько растянется, груз сместится вниз, после чего приобретет ускорение, равное ускорению лифта. В инерциальной системе отсчета, связанной с Землей (скажем, относительно стенок шахты лифта), груз приобретает ускорениепод действием раз­ности возросшей упругой силы пружины, тянущей ее вверх, и силы тяжести G, направленной вниз. С учетом знаков сил второй закон динамики запишется в виде

Когда груз приобретет то же ускорение, что и лифт, то

Сила натяжения пружины:

В системе отсчета, движущейся вместе с лифтом, на груз дей­ствуют сила тяжести G и упругая сила растянутой пружины причем теперь, что мы обнаруживаем по показаниям дина­мометра. Но хотя равенство междуи G нарушено, груз, когда растяжение пружины? достигает некоторой максимальной величины, остается в покое. Следовательно, в условие равновесия груза мы должны ввести силу инерции — jom с учетом знаков:

Откуда сила натяжения пружины равна:

Если ускорение лифта направлено вниз, то в начале движения точка подвеса приближается к грузу, который некоторое время пе­ремещается с ускорением, и сила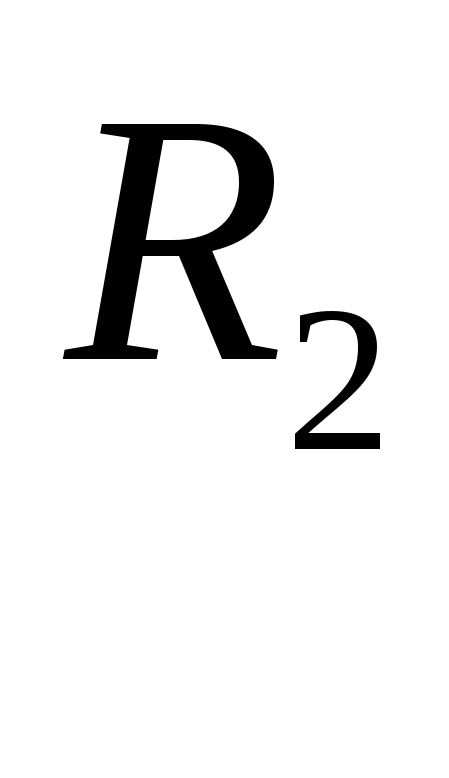, действующая со стороны пружины на груз, уменьшается (так как уменьшается деформация пружины). Возникшее превышение величины силы тяжести G над величиной упругой силысообщает грузу ускорение, равное ускорению лифта.Уравнение движения относительно неподвижной системы от­счета запишется на основании второго закона динамики в виде

Когда груз приобретет то же ускорение, что и лифт, уравнение движения примет вид:

так как /'=0.

Натяжение пружины равно:

Относительно системы отсчета, связанной с лифтом, груз нахо­дится в покое, хотя вес его теперь не уравновешен упругой силой. Следовательно, вес груза частично уравновешивается силой инер­ции.

Откуда сила натяжения пружины равна:

Заметим, что в случае, если лифт движется с ускорением, рав­ным ускорению свободного падения jo=g, сила натяжения пружины обращается в нуль (тело становится невесомым). Так как в непод­вижной системе отсчета лифт, пружина и груз движутся с одина­ковым ускорением, то не возникает их перемещений друг относи­тельно друга, а следовательно и взаимодействий.

В системе, связанной с лифтом, наступление состояния невесо­мости свидетельствует о том, что переносное ускорение стало равно ускорению силы тяжести.

Таким образом, задача о движении тела относительно неинерциальной системы отсчета решается и первым и вторым способом. Принципиальной разницы между ними нет.

Отметим следующую особенность сил инерции в неинерциальных системах — особенность, которая только и отличает их от всех других сил: силы инерции не имеют противодействующей силы, так как нельзя указать тела, со стороны которого они приложены. Воз­никновение сил инерции также результат передачи движения, но не данному телу, а телам отсчета, относительно которых изучается движение тела.

Рис.2

Рассмотрим диск, вращающийся вокруг перпендикулярной к нему вертикальной оси z' с угловой скоростью (рис. 2).Вместе с диском вращается надетый на спицу шарик, соединенный с центром диска пружиной. Шарик занимает на спице такое положение, при котором сила натя­жения пружины F_np оказывается равной произ­ведению массы шарика т на его ускорение w_n= -R , R — радиус-вектор, прове­денный к шарику из центра диска, его модуль R дает расстояние шарика от центра диска (6)

Относительно системы отсчета, связанной с диском, шарик по­коится. Это можно формально объяснить тем, что, кроме силы (6), на шарик действует сила инерции направленная вдоль радиуса от центра диска.

(7)

Силу инерции (7), возникающую во вращающейся (по отно­шению к инерциальным системам) системе отсчета, называют центробежной силой инерции. Эта сила действует

натело во вращающейся системе отсчета, независимо от того, покоится тело в этой системе

или движется относительно нее со скоростью v'.

Рис.3

Если положение тела во вращающейся системе отсчета характе­ризовать радиусом-вектором г', центробежную силу инерции мож­но представить в виде двойного векторного произведения:

(8)

Действительно, вектор b=[r', ] направлен перпендикулярнок векторам и F_u6 «на нас» (рис.3) и равен по модулю r' sinR/ Векторное произведение взаимно перпендикулярных векто­ров m и b совпадает по направлению с F_u6 и имеет модуль, равный mb= mR= F_uб