Лекция №10.

Пара сил. Момент пары. Закон сохранения момента импульса твердого тела и примеры его проявления. Вычисление моментов инерции тел . Теоремы Штейнера-Гюйгенса. Кинетическая энергия вращательного движения .

Пара сил — это две равные по величине и противоположные по направлению параллельные силы, приложенные к одному телу. Пара сил не имеет равнодействующей. Кратчайшее расстояние между линиями действия сил, образующих пару сил, называют плечом пары. Действие пары сил на тело характеризуется моментом пары сил — произведением одной из сил на плечо.

Найдем значение вектора момента пары сил.

Положим, к телу приложена пара сил и. Рассечем тело плоскостью, в которой лежат силы (рис. 3).

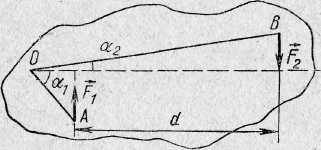
рис. № 3. Момент пары сил.

Возьмем произволь­ную точку О, лежащую в этой плоскости. Момент силы относи­тельно этой точки M₁=F₁OAи направлен перпендикулярноплоскости чертежа к нам. Момент силы равен M₂=F₂OBи направлен перпендикулярно плоскости чертежа от нас Суммарный момент пары сил равен алгебраической сумме моментов M_t и М₂:

M=.

Но поскольку ,

.

Выражение, стоящее в скобках, представляет собой расстояние между линиями действия сил. Обозначим это расстояние через

Тогда

,

где d — плечо пары сил.

Вектор момента пары сил численно равен произве­дению величины одной из сил пары на плечо пары. Он направлен в сторону поступательного движения бу­равчика, рукоятка которого вращается по направле­нию сил пары.

В механике имеется три закона сохранения: импульса, энергии и момента импульса. Все они являются следствиями законов движения. Ограничимся лишь простыми частными случаями.

Если при вращении тела вокруг неподвижной оси момент внешних сил относительно этой оси равен нулю, то равна нулю производная момента импульса тела:

Это означает, что сам момент импульса остается постоянным:

Из неизменности момента инерции J твердого тела, вращающегося вокруг определённой оси, следует постоянство угловой скорости вращения. Так, если бы не было трения, то не менялась бы угловая скорость вращающегося на оси колеса.

Последнее уравнение и является формой закона сохранения момента импульса для частного случая вращения вокруг неподвижной оси. В общем случае этот закон формулируется так: в замкнутой системе тел полный (суммарный) момент импульса остаётся постоянным.

Если момент внешней силы, действующей на тело, равен нулю, то уравнение выполняется и в том случае, когда тело не является твёрдым, т.е. когда момент его инерции может изменяться. Причём в этом случае закон сохранения момента импульса позволяет простым путём получить важные заключения о характере вращения тела.

Все вы могли видеть, как балерина или конькобежец-фигурист легко меняет скорость своего вращения , не отталкиваясь от пола или льда. То же явление можно наблюдать и по-другому. Человек становится на круглую платформу, которая может вращаться вокруг вертикальной оси без заметного трения (скамья Жуковского). Оттолкнувшись затем от пола, он начинает вращаться, Меняя затем положение рук (лучше с тяжёлыми предметами в ладонях), т.е. меняя момент инерции тела, человек тем самым меняет и угловую скорость вращения,

Для вычисления момента инерции необходимо мысленно рас­членить тело на достаточно малые элементы, точки которых можно считать лежащими на одинаковом расстоянии от оси вращения, затем найти произведение массы каждого элемента на квадрат его расстояния от оси и, наконец, просуммировать все полученные про­изведения. Очевидно, это весьма трудоемкая задача. Для подсчета моментов инерции тел правильной геометрической формы можно воспользоваться в ряде случаев приемами интегрального исчисле­ния .

Нахождение конечной суммы моментов инерции элементов тела заменим суммированием бесконечно большого числа моментов инер­ции, вычисленных для бесконечно малых элементов:

.

Вычислим в качестве примера момент инерции однородного диска или сплошного цилиндра высотой h относительно его оси симметрии (рис. 4).

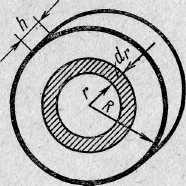
рис.№4 Вычисление момента инерции однородного диска

Расчленим диск на элементы в виде тонких концентрических колец с центрами на оси его симметрии. Полученные кольца имеют внутренний диаметр r и внешний r-dr, а высоту h. Так как dr<<r, то можем считать, что расстояние всех точек кольца от оси равно r. Для каждого отдельно взятого кольца момент инерции где , — масса всего кольца.Объем кольца . Если плотность мате­риала диска , то масса кольца.

Момент инерции кольца .Чтобы подсчитать момент инерции всего диска, надо просуммировать моменты инерции колец от центра диска () до края его(r=R),

т. е. вычислить интеграл:

или

Но масса диска , следовательно,

Приведем (без вычисления) моменты инерции для некоторых тел правильной

геометрической формы, выполненных из однород­ных материалов (рис. 5).

1. Момент инерции тонкого кольца относительно оси, проходя­щей через его центр перпендикулярно его плоскости (или тонко­стенного полого цилиндра относительно его оси симметрии):

2. Момент инерции толстостенного цилиндра относительно оси симметрии:

где — внутренний иR₂— внешний радиусы.

3. Момент инерции диска относительно оси, совпадающей с од­ним из его диаметров:

4. Момент инерции сплошного цилиндра относительно оси, пер­пендикулярной образующей и проходящей через ее середину:

,

где R — радиус основания цилиндра, h — высота цилиндра

5. Момент инерции тонкого стержня относительно оси, прохо­дящей через его середину:

,

где — длина стержня.

6 Момент инерции тонкого стержня относительно оси, прохо­дящей через один из его концов:

7. Момент инерции шара относительно оси, совпадающей содним из его диаметров:

рис.№5 К расчёту моментов инерции различных тел:

1—кольца относительно оси, проходящей через центр перпендикулярно его плоскости; 2 — полого цилиндра относительно оси симметрии, параллельной образующим; 3 — тонкого диска относительно оси, совпадающей с диаметром; 4 — сплошного цилиндра относитель­но оси симметрии, перпендикулярной образующим; 5 — однородного стержня относитель­но оси, проходящей через середину перпендикулярно к нему; 6 — однородного стержня от­носительно оси, проходящей через конец стержня; 7 — шара относительно оси, совпадаю­щей с диаметром.

Если известен момент инерции какого-либо тела относительно оси, проходящей через его центр масс, то момент инерции относи­тельно любой другой оси, параллельной первой, может быть найден на основании так называемой теоремы Гюйгенса:

Момент инерции тела J относительно любой оси равен моменту инерции тела относительно оси, параллельной данной и проходящей через центр масс тела, плюс масса тела т, умноженная на квадрат расстояния между осями:

Кинетических энергия твердого тела конечных размеров равна сумме кинетических энергий элементов, на которые расчленено тело. В общем случае тело может двигаться поступательно и однов­ременно вращаться. Рассмотрим частный случай вращения тела

вокруг неподвижной оси.

Кинетическая энергия каждого элемента тела:

(**)

де m_i—масса -го элемента тела,— его линейная скорость .

Если расстояние центра элемента от оси вращения то, при­нимая во внимание, что , равенство (**) перепишем в виде:

и, просуммировав по всем элементам, получим:

Но так как — момент инер­ции тела относительно выбранной оси, то

Эта формула отличается от соответствующей формулы для поступательного движения тем, что вместо линейной скорости в ней стоит угловая скорость, а вместо массы — момент инерции.

Рассмотрим изменение кинетической энергии вращающегося тела под действием сил. Положим, тело вращается вокруг непод­вижной оси 00. Пусть результирующая сила F, приложенная в точке А тела, отстоящей от оси на расстоянии r, лежит в плоскости траектории точки и направлена по касательной к ней (рис. 6).

рис.№6 К расчету работы при вращательном движении.

При повороте тела на угол точка приложения силы переме­стится на длину дуги . Если угол достаточно мал, то дугуds мож­но считать равной перемещению ds. Тогда

элементарная работа силыF на пути ds:

но

,

Так как

то

Полная работа при повороте на угол :

Если момент равнодействующей всех сил — величина постоянная, то из последнего соотношения получим:

При вращательном движении работа измеряется про­изведением момента силы на угол поворота тела.

Если момент силы меняется со временем, то работа измеряется интегралом от момента силы по углу поворота.

Напишем основное уравнение динамики вращательного движе­ния:

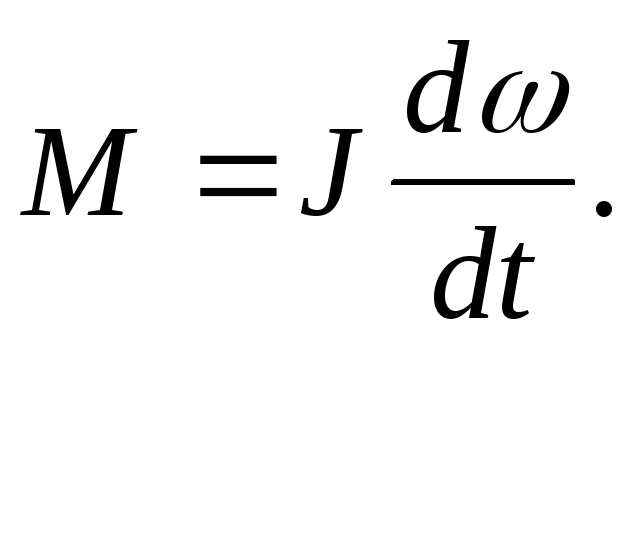
Для подсчета работы умножим обе части равенства на угол поворота где—угловая скорость вращения иdt—весьма малый интервал времени , в пределах которого можно считать М=const:

Проинтегрировав левую и правую части последнего равенства, получи:

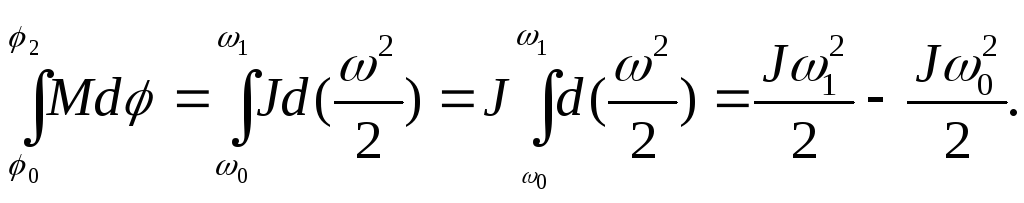
Т.е. изменение кинетической энергии тела при вращательном движении равно работе сил, момент которых сообщает телу угловое ускорение.

Полная кинетическая энергия твердого тела равна сумме кинетической энергии поступательного движения центра масс тела и кинетической энергии вращения тела:

,

где — скорость поступательного движения центра масс,J—момент инерции тела относительно оси вращения , проходящей через центр масс, —угловая скорость вращения тела вокруг своей оси.

Лекция11.

Понятие о твердом теле, которое вращается вокруг неподвижной точки. Свободные оси вращения. Гироскоп. Условия равновесия твердого тела. Виды равновесия.

При поступательном движении все точки твердого тела совершают равные перемещения за один и тот же промежуток времени. Поэтому скорости и ускорения всех точек тела в данный момент времени одинаковы. Этот факт позволяет свести изучение поступательного движения твердого тела к изучению движения отдельной частицы тела, т. е. к задаче кинематики частицы. Таким образом, поступательное движение твердого тела может быть полностью описано, если известны зависимость от времени радиус-вектора любой точки этого тела и его положение в начальный момент.

Рассмотрим вращение твердого тела вокруг неподвижной оси .

.

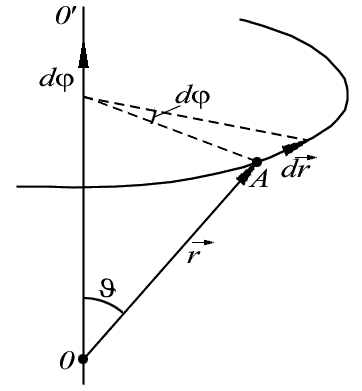
РИС.№1 Вращение твердого тела вокруг неподвижной оси.

Пусть твердое тело, вращаясь вокруг нее, совершило за время бесконечно малый поворот. Угол поворота будем характеризовать вектором,модуль которого равен углу поворота , а направление совпадает с осью 00', причем так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора (рис.1). Векторназываетсяаксиальным вектором, тогда как вектор перемещения являетсяполярным вектором (к ним также относятся векторы скорости и ускорения). Они отличаются тем, что полярный вектор кроме длины и направления имеет точку приложения (полюс), а аксиальный вектор имеет только длину и направление, но не имеет точки приложения. Векторы такого типа часто применяются в физике. К ним, например, относятся все вектора, являющиеся векторным произведением двух полярных векторов.

     Найдем элементарное перемещение любой частицы А твердого тела при таком повороте. Положение частицы А зададим радиус-вектором , проведенным из некоторой точки О на оси вращения. Тогда линейное перемещение конца радиус-векторасвязано с углом поворотасоотношением (рис. 2.6)

     или в векторном виде

     Заметим, что это равенство справедливо лишь для бесконечно малого поворота ,то есть только бесконечно малые повороты можно рассматривать как векторы. Для конечного поворота на уголлинейное перемещение частицы А определяется формулой:

     Очевидно, что перемещение нельзя представить как векторное произведение векторов и, так как это возможно лишь при бесконечно малом повороте, когда радиус-векторможно считать неизменным.

     Можно показать, что введенный вектор удовлетворяет основному свойству векторов - векторному сложению. Пусть твердое тело совершает два элементарных поворота₁ и ₂ вокруг разных осей, проходящих через неподвижную точку О. Тогда суммарное перемещение произвольной частицы А тела, радиус-вектор которой относительно точки О равен, можно представить так:

     

,

     где

     Мы доказали, что два поворота, ₁ и ₂, эквивалентны одному повороту на угол вокруг оси, совпадающей с вектороми проходящей через точку О.

     Введем теперь векторы угловой скорости и углового ускорения таким же способом, как мы вводили векторы и. Вектор угловой скоростиопределяют так

 где dt - интервал времени, за который тело совершает поворот . Векторсовпадает по направлению с вектороми является аксиальным вектором.

     Изменение вектора со временем характеризуют вектором углового ускорения, который определяют соотношением,

     Направление вектора совпадает с направлением- приращения угловой скорости. Вектор, как и, также аксиальный.

Представление угловой скорости и углового ускорения в виде векторов очень полезно при изучении более сложных движений твердого тела. Это позволяет во многих случаях получить большую наглядность, а также резко упростить как анализ движения, так и соответствующие расчеты.

     Представим выражения для угловой скорости и углового ускорения в проекциях на ось вращения Оz, положительное направление которой свяжем правилом правого винта с положительным направлением отсчета координаты (рис. 2).

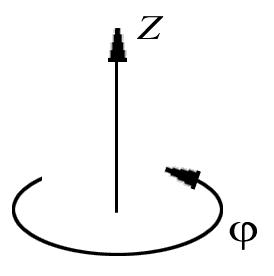
РИС.№2 Введение понятия угловых векторов

Тогда проекции ивекторовина осьопределяются формулами: (*)

 В этих формулах и- алгебраические величины. Их знак характеризует направление соответствующего вектора. Например, если, то направление векторасовпадает с положительным направлением оси z. Если, то и направление векторапротивоположно. Аналогично правило верно для углового ускорения.

     По известной зависимости , называющейсязаконом вращения тела, формулы (*) дают возможность определить угловую скорость и угловое ускорение в любой момент времени. Из зависимости углового ускорения от времени и начальных условий, т. е. угловой скорости и угла ( в начальный момент времени, можно найтии.

     Пусть твердое тело вращается вокруг неподвижной оси по закону , гдеи- некоторые положительные постоянные. Определим движения тела.

     Согласно (*) , . Из этих соотношений видно, что тело вращается равнозамедленно (), останавливается в момент времени, а затем начинает вращаться в противоположном направлении ().

     Легко заметить, что все задачи на вращение твердого тела вокруг неподвижной оси аналогичны по форме задачам на прямолинейное движение частицы. Достаточно заменить линейные величины x, ина соответствующие угловые,и, как получаются все закономерности и соотношения для вращающегося тела.

Связанные с телом оси, при вращении относительно которых динамические реакции опор равны статическим, называются свободными осями.

Теоретическое исследование показывает, что в любом теле произвольной формы существуют три взаимно перпенди­кулярные оси, проходящие через центр масс тела, кото­рые могут служить свободными осями вращения. Их на­зывают главными осями инерции.

Для тел правильной формы эти оси находятся легко. Для прямоугольного параллелепипеда (папиросной коробки) глав­ные оси инерции — это оси, проходящие через центры противопо­ложных граней (рис. 3). Для однородных тел вращения главные оси инерции представляют собой оси геометрической симметрии. Для эллипсоида вращения свободными осями будут большая и малая оси и ось, перпендикулярная к ним..

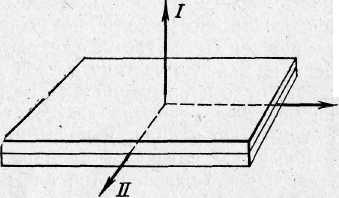
рис. № 3 Главные оси вращения параллелепипеда.

Тело, вращающееся вокруг свободной оси, в отсутствие момента внешних сил относительно центра тяжести должно вращаться не­ограниченно долго, сохраняя неизменным положение оси. Однако создать вращение точно вокруг главной оси практически не удается, так как центр масс оказывается, хотя и ненамного, смещенным от­носительно оси вращения. При больших скоростях вращения даже небольшое смещение может создать значительные динамические нагрузки.

Поэтому существенным является вопрос об устойчивости вра­щения вокруг главных осей, т. е. вопрос о том, будет ли возникшее малое уклонение от вращения вокруг свободной оси в дальнейшем возрастать или тело будет стремиться под действием возникших динамических реакций вер­нуться к вращению вокруг главной оси. Устойчивость того или другого конкретного вида движения — сложнейший вопрос меха­ники, для поисков ответа на который пока еще не существует единого метода.

В теоретической механике показано, что в отсутствие внешних сил устойчиво вращение относительно главных осей, соответствующих наибольшему и на­именьшему моментам инерции тела. Вращение вокруг главной оси, соответ­ствующей среднему моменту инерции, неустойчиво.

Устойчивость вращения вокруг главных осей инерции можно продемонстрировать, вращая различные тела с помощью центро­бежной машины (рис. 104).

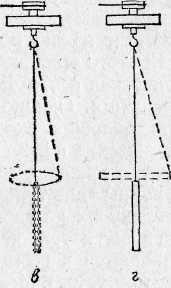
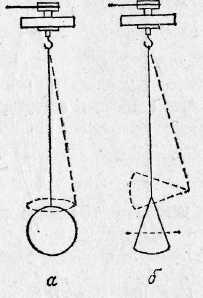
рис. № 4 Вращение вокруг главных осей инерции.

Подвешенная за один из концов палочка при малых скоро­стях вращается в вертикальном положении (рис.4, г), т. е. вокруг оси с наименьшим моментом инерции. При возрастании скорости палочка вопреки действию силы тяжести рас­полагается горизонтально и устойчиво вра­щается вокруг оси с наибольшим моментом инерции.

Вообще, практически оказывается, что вращение устойчиво вокруг оси с наи­большим моментом инерции. Это связано с влиянием внешних сил, в частности сил трения, которые создают момент относительно центра тяжести. Действие этого момента в случае вращения вокруг оси с наибольшим моментом инерции оказывается меньшим.

Ось с наименьшим моментом инерции интересна тем, что относительно нее легче всего создать вращение.

Падающая кошка, например , как известно, из любого положе­ния встает на лапки. Для этого кошка в воздухе вращает хвостом и лапками так, чтобы в силу закона сохранения момента количества движения повернуться вокруг го­ризонтальной оси, относительно которой у кошки наименьший мо­мент инерции.

При изучении вращения твердого тела, имею­щего закрепленную точку, следует различать не совпадающие друг с другом: 1) ось вращения тела; 2) мгновенную ось вращения; 3) на­правление, или ось момента количе­ства движения. Даже рассматривае­мый частный случай движения тела, имеющего неподвижную точку, до­вольно сложен. Мы ограничимся при­ближенным изучением одного, еще более частного, но имеющего широкое научное и техническое применение случая. Рассмотрим приближенную теорию гироскопа.

Гироскопом называют мас­сивное однородное тело враще­ния, быстро вращающееся отно­сительно одной из главных осей инерции.

Из определения следует, что гиро­скоп обладает осью симметрии (пос­кольку он является телом вращения), которая служит одной из главных осей инерции (поскольку материал ги­роскопа однороден). Обычно за ось вращения гироскопа выбирается главная ось инерции, которой соответствует максимальный момент инерции. Эту ось будем назы­вать осью гироскопа.

Допустим, ось гироскопа при его вращении остается неподвижной. Следовательно, вектор мгновенной угловой скорости лежит на этой оси. Вектор момента количества движения также направлен вдоль оси гироскопа. Таким образом, ось гироскопа, мгно­венная ось вращения и ось момента количества движения в этом случае совпадают. В реальных условиях ось гироскопа лишь при­ближенно может считаться главной осью инерции, так как центр масс гироскопа всегда хоть немного смещен относительно оси сим­метрии. Кроме того, как мы увидим ниже, ось не может оставаться неподвижной, не будучи закрепленной в подшипниках, так как мы не в силах полностью избавиться от трения.

Положим, гироскоп имеет очень большую угловую скорость вращения вокруг собственной оси ОО¹ и в то же время ось медленно вращается с угловой скоростью вокруг неподвижной вер­тикальной оси (рис.5).

Направление мгновенной оси враще­ния определяется вектором мгновенной угловой скорости результирующего вращения . Как видно из чертежа (вследствиетого, что), мгновенная ось вращения лежит вблизи оси ги­роскопа.

Построив вектор момента количества движения ,

где и — моменты инерции гироскопа относительносоответствующих осей, можно убедиться, что и ось момента коли­чества движения лежит вблизи оси гироскопа (рис.5) (При построении вектора надо иметь в ви­ду, что хотяиимеют разную величину, одна­ко порядок их величины одинаков.)

рис.№5. Вращение тела вокруг оси, закрепленной в одной точке , когда скорость вращения тела много больше скорости обращения.

Таким образом, при вращении реального гиро­скопа ось его, мгновенная ось вращения и ось мо­мента количества движения хотя и не совпадают, но расхождение их направлений незначительно.

В основу приближенной теории гироскопа, ко­торую мы рассмотрим ниже, кладется допущение, что все три указанные оси совпадают и неизмен­но связаны друг с другом. Другими словами, если мы видим, что ось гироскопа как-то изменяет свое положение в пространстве, мы считаем себя вправе сделать заключение, что также меняется в пространстве нап­равление мгновенной угловой скорости вращения гироскопа и оси его момента количества движения.

И обратно, установив, что в силу каких-то причин (о них будет сказано ниже) вектор момента количества движения должен изме­нить свое положение, мы будем считать, что вместе с ним изменит свое положение и ось гироскопа. Уравнение , для случая вращения телавокруг неподвижной оси, справедливо и для движения гироскопа. Доказательство этого утверждения можно найти в курсе теорети­ческой механики.

Из равенства следует, что вектор момента количествадвижения изменяется только при действии на гироскоп момента внешних, сил. И так как мы допускаем, что ось гироскопа и ось момента количества движения жестко связаны, мы можем утвер­ждать, что и перемещение оси гироскопа происходит пока действует момент внешних сил.

Чтобы сделать вра­щение гироскопа свободным от влияния внешних сил, необходимо свести к минимуму силы трения, действующие на гироскоп, и устранить действие силы тяжести. Уменьшение силы трения дос­тигается особой конструкцией и обработкой оперных подшипников, в которые помещается ось гироскопа. Для устранения действия силы тяжести гироскоп заставляют вращаться вокруг оси, прохо­дящей через центр масс. Тогда результирующая силы тяжести все время лежит на оси вращения, и момент ее равен нулю.

Свободный гироскоп имеет форму «колокольчика» с утя­желенным краем (рис. 6).

рис.№6 Гироскоп, имеющий форму «колокольчика»

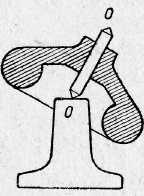
Центр тяжести такого гироскопа на­ходится внутри «колокольчика», и с ним совмещается конец оси 00. В технике чаще всего при создании свободного гироскопа используется карданов подвес ( рис.№7)

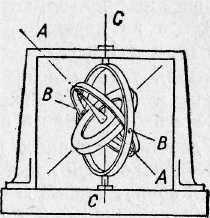рис.№7 Гироскоп на кардановом подвесе.

Свободное твердое тело имеет шесть степеней свободы. Для описания поступательного движения его центра масс и вращения тела вокруг трех осей, проходящих через центр масс, мы можем составить шесть уравнений. Три из них, полученные на основе закона движения центра масс твердого тела:

связывают координаты x, у, z центра масс тела с составляющими ре­зультирующей внешних сил по осям х, у, z.

Другие три уравнения, полученные из основного закона дина­мики вращающегося твердого тела:

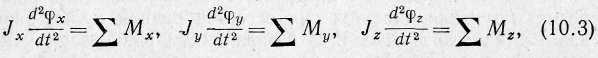
связывают углы поворота тела вокруг осей x, у, z с моментами внеш­них сил относительно тех же осей.

Для того чтобы тело находилось в равновесии, т. е. не переме­щалось вдоль осей и не вращалось вокруг них, необходимо выпол­нение следующих шести условий:

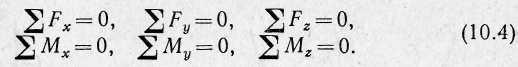
Для равновесия твердого тела, находящегося под дей­ствием произвольной системы сил, необходимо, чтобы сумма проекций всех сил на оси координат и сумма мо­ментов этих сил относительно осей координат были равны нулю.

Если в данный момент тело находится в равновесии, то это не служит гарантией того, что оно останется в таком состоянии как угодно долго. В реальных условиях на всякое тело действуют слу­чайные толчки, устранить которые принципиально невозможно. Чтобы выяснить, могут ли эти толчки вывести тело из состояния рав­новесия или нет, надо исследовать, как изменяется результирующая сил, действующих на тело, при малом его отклонении от положения равновесия.

Положим, тело (шарик) находится в покое на дне гладкой ямы (рис. 7), в нижней точке которой на него действуют равные и противоположно направленные силы mg и R (их результирующая равна нулю). Отклоним шарик от положения равновесия. Теперь на него действует результирующая F сил mg и ,уже не равная нулю. Она направлена к положению равновесия, куда и возвратит шарик, когда перестанет действовать отклоняющий фактор. Если при малом от­клонении тела от положения равновесия результирующая внешних сил не вызывает увеличения начального отклонения, то тело на­ходится в устойчивом равновесии.

Положим, шарик находится в равновесии на вершине" гладкого купола (рис. 8). При этом силы, mg и R опять уравновешивают друг друга, и их результирующая равна нулю. При малейшем от­клонении шарика от положения равновесия возникает результиру­ющая F, отличная от нуля и удаляющая шарик от положения равновесия.

Если результирующая сила, возникающая при отклонении тела от положения равновесия, увеличивает начальное отклонение, рав­новесие тела называется неустойчивым.

И наконец, если при смещении тела от положения равновесия результирующая внешних сил остается равной нулю, равновесие называется безразличным. В безразличном равновесии находится, например, покоящийся на гладкой горизонтальной плоскости ша­рик.

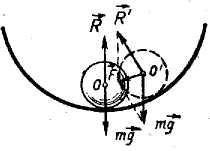
рис.№7 Устойчивое равновесие. Рис.№8 Неустойчивое равновесие.

Состояние равновесия системы тел, на которую действуют внеш­ние консервативные силы, устойчиво только в том случае, если ему соответствует минимум потенциальной энергии.

Допустим, что система, находящаяся под действием консерва­тивных сил в состоянии равновесия, обладает минимумом потен­циальной энергии. Значит, при любом отклонении от этого поло­жения ее потенциальная энергия возрастает. Но в соответствии с законом сохранения энергии полная энергия консервативной сис­темы, равная сумме кинетической Е_k и потенциальной U энергии, остается постоянной:

U=const.

Следовательно, если в начальный момент времени все тела системы находились в покое, то движение может возникнуть лишь как ре­зультат перехода части потенциальной энергии в кинетическую {так как всегда >0). Если же в начальный момент потенциальнаяэнергия минимальна, то движение возникнуть не может и система находится в состоянии устойчивого равновесия.

При безразличном равновесии потенциальная энергия одина­кова для близких положений тел системы.

В поле силы тяжести тело обладает минимумом потенциальной энергии, когда его центр тяжести занимает наинизшее положение. Таким образом, состояние устойчивого равновесия тела в поле силы тяжести соответствует наинизшему положению его центра тяжести.

Лекция 12.Закон тяготения Ньютона, постоянная тяготения и ее измерение. Гравитационная и инертная масса тела. Понятие о поле тяготения. Гравитационное поле. Однородное и центральное поле. Напряженность и потенциал поля тяготения.

Закон всемирного тяготения.

Сам факт существования в природе гравитационного взаимо­действия (называемого еще всемирным тяготением) и закон, ко­торому подчиняется это взаимодействие, были открыты Ньюто­ном и опубликованы им в 1686 г. в упоминавшемся уже труде «Математические начала натуральной фи­лософии».

Всемирное тяготение состоит в том, что всем телам природы присуще свой­ство притягивать друг друга. Закон все­мирного тяготения формулируется так. Сила взаимного притяжения двух мате­риальных точек прямо пропорциональна произведению масс взаимодействующих точек и обратно пропорциональна квад­рату расстояния между ними:

(1)

где— коэффициент пропорциональности, зависящий от выбора единиц измерения входящих в формулу величин.

Взаимодействие неточечных (протяженных) тел представ­ляет собой суммарный результат взаимодействия между отдель­ными элементами (точками) взаимодействующих тел.

Рис.1

Гениальность Ньютона проявилась здесь в том, что он по­ставил и правильно решил такой вопрос: есть ли взаимное при­тяжение протяженных тел их свойство как протяженных тел или же оно есть результат взаимодействия составляющих эти тела элементов масс. Ньютон ответил на этот вопрос гениальной догадкой в пользу последнего и поэтому сформулировал свой закон для материальных точек. Не имея этого фундаментального закона, трудно было бы разобраться во взаимодействиях про­тяженных тел, так как в этом случае сила взаимодействия зави­сит также от размеров и формы тел.

Закону всемирного тяготения (1) можно придать вектор­ную форму. Для этого договоримся определять положение вто­рой материальной точки, относительно первой, радиус-вектором, проведенным от т₁ к m₂ (рис.1).

Введем единичный вектор вдоль вектора. Тогда

Очевидно, что сила, с которой точка массы т₁ действует на точку массы m₂, запишется так:

.

где знак минус указывает на то, что вектор противоположен вектору. Таким образом, силу можно записать в векторной форме следующим образом:

(2)

Рассказывают, будто упавшее с дерева яблоко навело Нью­тона на размышления, которые привели к открытию закона все­мирного тяготения. Возможно, что это и так. Но бесспорно, что при таком (или подобном) наблюдении Ньютону пришла уди­вительная мысль: не является ли сила, удерживающая Луну на орбите, силой той же природы, что и сила, заставляющая тело падать на поверхность Земли, но лишь ослабленной за счет рас­стояния? Сопоставляя центростремительное ускорение Луны и ускорение свободного падения тел на поверхности Земли, Нью­тон немедленно пришел к выводу, что если причинa падения тел на Землю и движения Луны одна и та же и состоит во взаим­ном притяжении тел, то сила, с которой тело притягивается к Земле, должна быть обратно пропорциональна квадрату рас­стояния до центра Земли. Распространив гипотезу о притяже­нии между телами на все тела солнечной системы, Ньютон смог объяснить, почему движение планет подчиняется трем законам Кеплера, почему этим же законам подчиняется движение спут­ников около планет (спутники Марса, Юпитера, Земли). На основе закона всемирного тяготения Ньютон также объяснил движение комет, образование морских приливов на Земле, воз­мущения в движении Луны. Далее Ньютон сделал обобщающее предположение, что взаимное притяжение тел — универсальное свойство и проявляется во всем окружающем нас мире. То, что взаимное тяготение тел не наблюдалось в обычных условиях нашей жизни (между окружающими нас телами), объясняется только тем, что сила взаимного притяжении для тел с неболь­шой массой очень мала и в обычных условиях перекрывается другими силами (например, трением). Однако, если создать спе­циальные условия, устраняющие трение, можно обнаружить и силы взаимного притяжения обычных тел. Это впервые проде­лал Кавендиш.

Ньютон опубликовал свой закон лишь спустя 16 лет после его открытия, когда ему удалось с помощью изобретенного им метода интегрального исчислении (а также для «убедительно­сти» и элементарным путем) решить задачу о силе взаимодей­ствия тонкого сферического слоя с материальной точкой, нахо­дящейся вне сферы.

Он показал, что сферический слой притягивает внешнюю точ­ку массы т так, как если бы вся масса М этого слоя была со­средоточена в центре сферы:

где r — расстояние материальной точки от центра сферы.

Из этого результата вытекает, что однородное тело шаровой формы притягивает внешнюю материальную точку так, как если бы вся его масса была сосредоточена в центре шара. Два же однородных шара притягиваются так, как если бы массы обоих шаров были сосредоточены в их центрах. Это значит, что шары взаимодействуют как материальные точки, массы которых равны массам шаров.