2. Потенциальная и кинетическая энергии

Установим изменение потенциальной и кинетической энергий колеблющейся системы. Известно, что потенциальная энергия упруго деформированного тела равна , гдеk - коэффициент упругости, х - смещение; откуда для потенциальной энергии колебаний находим

. (7)

Кинетическая энергия , что, согласно (2) и (5), в нашем случае будет

. (8)

Анализ (7) и (8) показывает, что когда одна из энергий илиувеличивается, то другая уменьшается. Полная же энергия

E=W_n+W_k=kA²/2 (9)

остается величиной постоянной и для пружинного маятника, (см. рис. 1), она определяется работой, совершенной внешней силой по сжатию или растяжению пружины. Итак, мы рассмотрели свободные или собственные колебания, которые происходят в системе, предоставленной самой себе, после того, как она была выведена из положения равновесия.

Но в реальных условиях всегда на механические системы действуют силы трения из-за чего свободные колебания переходят в затухающие, которые будут рассмотрены в параграфе 8.

3. Векторная диаграмма гармонического колебания

Гармоническое колебание

можно представить в виде проекции вектора , вращающегося против хода часовой стрелки с угловой скоростью, равной круговой частоте . Из рис. 3 следует, что проекция вектора на направлениеОХ будет.

4. Комплексная форма представления колебаний

С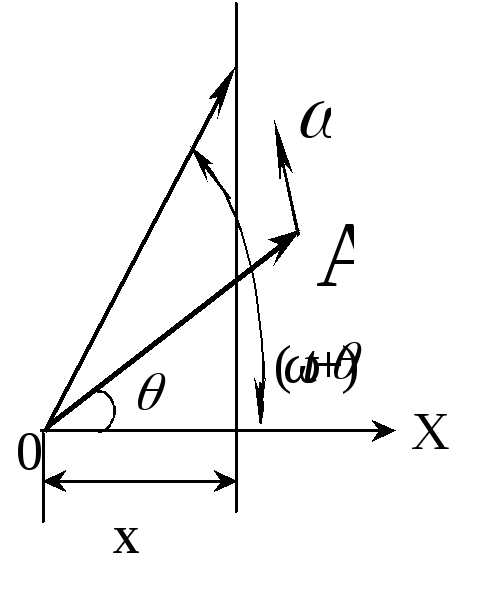огласно формуле Эйлера для комплексных чисел

, где .

Поэтому уравнение гармонического колебания (3) можно записать в экспоненциальной форме:

Рис. 3

.

Вещественная часть представляет собой смещениех при гармоническом колебании .

Обычно обозначение опускают и пишут так

.

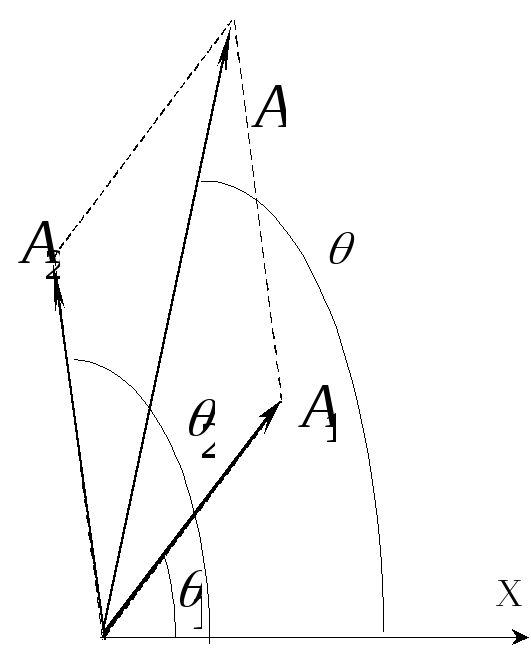
5. Сложение одинаково направленных колебаний

Рассмотрим сложение двух гармонических колебаний одинаковой частоты, смещения которых и.

Используем векторную диаграмму, рис. 4; откуда следует, что где

Рис. 4

.

Пусть , тогда

, т.е. результирующее колебание не будет гармоническим. Если колебания мало отличаются по частоте, например,,, то результирующее колебаниеможно рассматривать как почти гармоническое колебание с частотойи медленно меняющейся амплитудой. Такие периодические изменения амплитуды называются биениями.

6 Рис. 4 Рис. 5 Рис. 6. Сложение взаимно перпендикулярных колебаний

6.1. Пусть и, тогда траекторией будет прямая линия, рис. 5: .

6.2. При и, траекторией будет эллипс, ( рис. 6):

(x²/A²)+(y²/B²)=1.

При разных частотах складывающихся колебаний результирующие траектории будут иметь более сложный вид.

Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу.

Биение

Особый интерес представляет случай, когда два скла­дываемых гармонических колебания одинакового напра­вления мало различаются по частоте. Как мы сейчас пока­жем, результирующее движение при этих условиях можно рассматривать как гармоническое колебание с пульсиру­ющей амплитудой. Такое колебание называется бие­ниями.

Обозначим частоту одного из колебаний буквойчастоту второго колебания через По условию Амплитуды обоих колебаний будем полагать одинаковыми и равными а. Чтобы не усложнять без на­добности формул, допустим, что начальные фазы обоих колебаний равны нулю. Тогда уравнения колебаний будут иметь следующий вид:

Складывая эти выражения и применяя тригонометриче­скую формулу для суммы косинусов, получаем

(во втором множителе пренебрегаем членомпо сравнению с и). График функции ( ) изображен на рис . График построен для

Заключенный в квадратные скобки множитель в фор­муле ( ) изменяется гораздо медленнее, чем второй множитель. Ввиду условия Асо <С и за то время, за кото­рое множитель cos (cjt) совершает несколько полных коле­баний, множитель, стоящий в квадратных скобках, почти не изменяется. Это дает нам основание рассматривать ко­лебание ( ) как гармоническое колебание частоты , амплитуда которого изменяется по некоторому периодиче­скому закону. Выражением этого закона не может быть множитель, стоящий в квадратных скобках, так как он изменяется в пределах от —2а до +2а, в то время как амплитуда по определению — положительная величина.

График амплитуды показан на рис. Аналитическое выражение амплитуды, очевидно, имеет вид

Функция ( ) — периодическая функция с частотой, в два раза превышающей частоту выражения, стоящего под знаком модуля

т. е. с частотой Дол .Таким обра­зом, частота пульсаций амп­литуды — ее называют час­тотой биений — равна разности частот складывае­мых колебаний.

Отметим, что множитель 2а cos (Auj/2t) не только определяет амплитуду, но и влияет на фазу колебания. Это проявляется, например, в том, что отклонения, соответ­ствующие соседним максиму­мам амплитуды, имеют противоположные знаки (см. точ­ки Mi и М2 на рис. .