Операции над бинарными отношениями. Бинарным отношением между элементами множеств a и b называется произвольное подмножество r  ab. Запись aRb (при a  a, b  b ) означает, что (a,b)  r .

Определены следующие операции над отношениями R AA:

R ^-1={(a,b): (b,a)R},

R S={(a,b): ( xA)(a,x)R & (x,b)R},

Rⁿ=R(R^n-1),

.

Пусть Id_A = {(a,a): aA}– тождественное отношение. ОтношениеR XX называется

1. рефлексивным, если(a,a)Rдля всех a  X,

2. антирефлексивным, если(a,a)Rдля всехa  X,

3. симметричным, если для всехa, b  Xверна импликация aRb bRa,

4. антисимметричным, еслиaRb & bRa  a=b,

5. транзитивным, если для всехa, b, c Xверна импликацияaRb & bRc  aRc,

6. линейным, для всехa, b  Xверна импликация ab  aRb  bRa .

Обозначим IdA через Id. Легко видеть, что имеет место следующее

Предложение 1.ОтношениеR  XX

1. рефлексивно  Id  R ,

1. антирефлексивно  RId=  ,

2. симметрично  R = R^-1 ,

3. антисимметрично  R  R^-1  Id ,

4. транзитивно  RR R,

5. линейно R Id  R^-1 = X  X.

Матрица бинарного отношения. ПустьA={a₁,a₂, …,a_m} иB={b₁,b₂, …,b_n} – конечные множества.Матрицей бинарного отношенияRABназывается матрица с коэффициентами

Пусть A– конечное множество, |A|=nиB=A. Рассмотрим алгоритм вычисления матрицы композицииT= RS отношенийR,SAA. Обозначим коэффициенты матриц отношенийR,SиTсоответственно черезr_ij,s_ijиt_ij. Поскольку свойство (a_i,a_k)Tравносильно существованию такогоa_jA, что (a_i,a_j)R и (a_j,a_k)S, то коэффициентt_ikбудет равен 1, если и только если существует такой индексj, чтоr_ij=1 иs_jk =1. В остальных случаяхt_ikравен 0. Следовательно,t_ik= 1 тогда и только тогда, когда. Отсюда вытекает, что для нахождения матрицы композиции отношений нужно перемножить эти матрицы и в полученном произведении матриц ненулевые коэффициенты заменить на единицы. Следующий пример показывает, как этим способом вычисляется матрица композиции.

Пример 2. Рассмотрим бинарное отношение наA={1,2,3}, равноеR={(1,2),(2,3)}. Запишем матрицу отношенияR. Согласно определению, она состоит из коэффициентовr₁₂=1 ,r₂₃=1 и остальныхr_ij= 0. Отсюда матрица отношенияRравна

.

Найдем отношение RR. С этой целью умножим матрицу отношенияRна себя

.

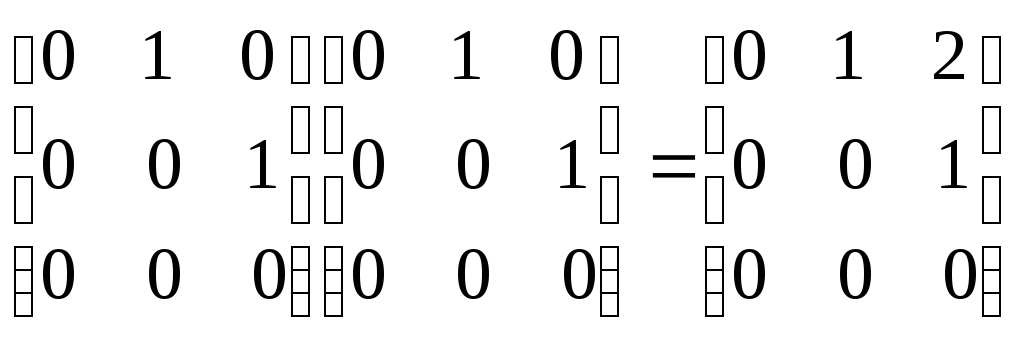Получаем матрицу отношения

.

Следовательно, RR={(1,2),(1,3),(2,3)}.

Из предложения 1 вытекает

Следствие 2. ЕслиA=B, то отношениеRнаA

1. рефлексивно, если и только если все элементы главной диагонали матрицы отношения Rравны 1,

2. антирефлексивно, если и только если все элементы главной диагонали матрицы отношения Rравны 0,

3. симметрично, если и только если матрица отношения Rсимметрична,

4. транзитивно, если и только если каждый коэффициент матрицы отношения RRне больше соответствующего коэффициента матрицы отношенияR.

1.6. Отношения порядка и эквивалентности

В данном параграфе изучаются частично упорядоченные множества и решетки. Рассматривается также отношения эквивалентности и их связь с разбиениями множества. Доказывается, что частично упорядоченное множество отношений эквивалентности на множестве является решеткой.

Определение 1. Пусть X – множество. Бинарное отношение R  XX называется отношением порядка на X, если оно рефлексивно, антисимметрично и транзитивно. Таким образом, R – отношение порядка, если

1. (a,a)R для всех a  X,

2. aRb & bRa  a=b,

3. для всех a, b, c  Xверна импликацияaRb & bRc aRc,

Пара (X,R), состоящая из множестваXи отношения порядкаRнаXназываетсячастично упорядоченным множеством.

Пусть (X,R) – частично упорядоченное множество. Всякое подмножествоAXбудет частично упорядоченным множеством с отношением порядкаR(AA).

Отношение порядка обычно обозначается символом .

Элемент xчастично упорядоченного множества (X,) называетсянаибольшим(соответственнонаименьшим), если для всякогоyXверноyx(соответственноxy).

Определение 2. Пусть (X,) – частично упорядоченное множество.Нижней граньюмножества его элементов называется наибольший элемент подмножества

.