Высшая матматика том2

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

Средняя кривизна. Кривизна дуги в точке. Радиус кривизны. Центр и круг кривизны. Эволюта и эвольвента. Свойства эволюты.

Кривизна пространственной кривой. Годограф.

Главная нормаль.

Вектор и радиус кривизны. Формулы Френе. Соприкасающаяся плоскость. Бинормаль.

Кручение кривой. Интегральное исчисление. Первообразная функция. Неопределенный интеграл.

Свойства неопределенного интеграла. Таблица основных интегралов. Непосредственное интегрирование. Способ подстановки. Интегрирование по частям. Интегрирование элементарных дробей. Рекуррентная формула.

Интегрирование рациональных функций. Интегрирование рациональных дробей. Метод неопределенных коэффициентов. Метод произвольных значений.

Интегрирование тригонометрических функций. Универсальная тригонометрическая подстановка. Интегрирование иррациональных функций.

Биноминальные дифференциалы. Тригонометрическая подстановка. Подстановки Эйлера.

Метод неопределенных коэффициентов.

Интегралы, не выражающиеся через элементарные функции. Эллиптические интегралы.

Интеграл Пуассона. Интеграл Френеля. Интегральный логарифм.

Интегральный синус и косинус. Определенный интеграл. Интегральная сумма. Интегрируемая функция. Свойства определенного интеграла. Теорема о среднем.

Обобщенная теорема о среднем. Вычисление определенного интеграла. Теорема Ньютона – Лейбница.

Замена переменных в определенном интеграле. Интегрирование по частям.

Приближенное вычисление определенного интеграла.

2

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

Формула прямоугольников. Формула трапеций. Формула парабол (Симпсона). Несобственные интегралы.

Абсолютная сходимость интеграла. Интеграл от разрывной функции. Нахождение площадей плоских фигур.

Нахождение площади криволинейного сектора. Вычисление длины дуги кривой.

Вычисление объемов тел по поперечным сечениям. Вычисление объемов тел вращения.

Площадь поверхности тела вращения. Функции нескольких переменных. Предел.

Непрерывность.

Наибольшее и наименьшее значения. Частное приращение.

Частная производная.

Геометрический смысл частных производных. Полное приращение и полный дифференциал. Касательная плоскость и нормаль к поверхности.

Приближенные вычисления с помощью полного дифференциала. Частные производные и дифференциалы высших порядков. Экстремум функции нескольких переменных.

Необходимые условия экстремума. Достаточные условия экстремума. Условный экстремум.

Функция Лагранжа. Производная по направлению. Направляющие косинусы. Градиент.

Связь градиента с производной по направлению. Кратные интегралы.

Двойные интегралы.

Условия существования двойного интеграла. Свойства двойного интеграла.

Вычисление двойного интеграла. Замена переменных в двойном интеграле. Якобиан.

Двойной интеграл в полярных координатах. Тройной интеграл.

Замена переменных в тройном интеграле. Цилиндрическая система координат. Сферическая система координат.

Геометрические и физические приложения кратных интегралов.

3

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

Дифференциальное исчисление функции одной переменной.

Производная функции, ее геометрический и физический смысл.

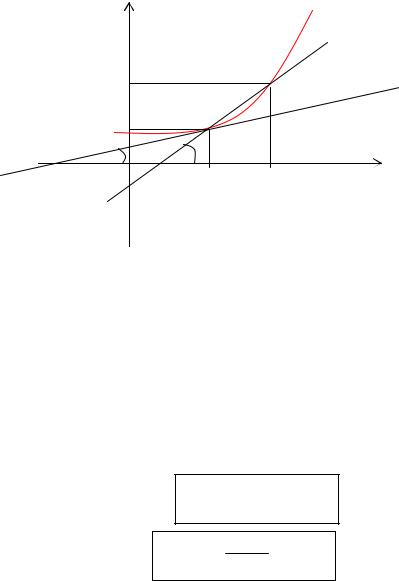
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.

у

f(x)

где α - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).

Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какойлибо точке.

Уравнение касательной к кривой: y − y0 = f ′(x0 )(x − x0 )

Уравнение нормали к кривой: y − y0 = − f ′(1x0 ) (x − x0 ) .

Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.

4

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.

Соответственно, вторая производная функциискорость изменения скорости, т.е. ускорение.

Односторонние производные функции в точке.

Определение. Правой (левой) производной функции f(x) в точке х = х0

Если функция f(x) имеет производную в некоторой точке х = х0, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Вопервых функция может иметь разрыв в точке х0, а вовторых, даже если функция непрерывна в точке х0, она может быть в ней не дифференцируема.

Например: f(x) = x - имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.

Теорема. (Необходимое условие существования производной) Если функция f(x)

имеет производную в точке х0, то она непрерывна в этой точке.

Понятно, что это условие не является достаточным.

Основные правила дифференцирования.

Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.

1)(u ± v)′= u′± v′

2)(u v)′= u v′+ u′v

3)u ′ = u′v −v′u , если v ≠ 0

v v2

Эти правила могут быть легко доказаны на основе теорем о пределах.

Производные основных элементарных функций.

5

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

Производная сложной функции.

Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.

Теорема доказана.

Способ логарифмического дифференцирования состоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле

6

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

f ′(x) = (ln f (x) )′ f (x)

Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных и показательностепенных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.

Производная показательностепенной функции.

Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.

Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0. Найдем производную функции y = uv. Логарифмируя, получим:

Производная обратных функций.

Пусть требуется найти производную функции у = f(x) при условии, что обратная ей функция x = g(y) имеет производную, отличную от нуля в соответствующей точке.

Для решения этой задачи дифференцируем функцию x = g(y) по х:

7

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

т.е. производная обратной функции обратна по величине производной данной функции.

Пример. Найти формулу для производной функции arctg.

Функция arctg является функцией, обратной функции tg, т.е. ее производная может быть найдена следующим образом:

Таким образом получены все формулы для производных арксинуса, арккосинуса и других обратных функций, приведенных в таблице производных.

Дифференциал функции.

Пусть функция y = f(x) имеет производную в точке х: yx = f ′(x)

Величина αΔx- бесконечно малая более высокого порядка, чем f′(x) x, т.е. f′(x) x- главная часть приращения у.

Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.

Обозначается dy или df(x).

Из определения следует, что dy = f′(x) x или

dy = f′(x)dx.

Можно также записать: f ′(x) = dydx

8

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

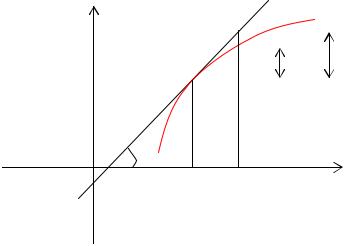
Геометрический смысл дифференциала.

y

α

Из треугольника MKL: KL = dy = tgα x = y′ x

Таким образом, дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.

Свойства дифференциала.

Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:

1)d(u ± v) = (u ± v)′dx = u′dx ± v′dx = du ± dv

2)d(uv) = (uv)′dx = (u′v + v′u)dx = vdu + udv

3)d(Cu) = Cdu

Дифференциал сложной функции. Инвариантная форма записи дифференциала.

Пусть y = f(x), x = g(t), т.е. у - сложная функция.

Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какойто другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.

Однако, если х - независимая переменная, то dx = x, но

9

=x cos x sin 2 x

= xex2 (1+ 2ln x + 2x2 ln x)

10