
Высшая матматика том2
.pdf
Ларин Александр Александрович “Курс высшей математики. Часть 2.”
Величина T1 называется кручением кривой.
Ниже рассмотрим несколько примеров исследования методами дифференциального исчисления различных типов функций.
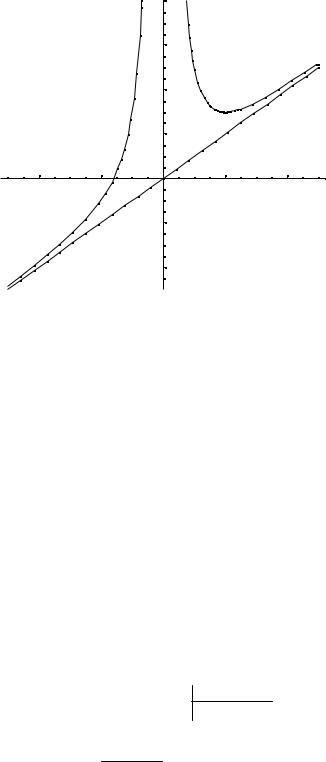
Пример: Методами дифференциального исчисления исследовать функцию y = 3 1− x3 и построить ее график.
1.Областью определения данной функции являются все действительные числа (-∞; ∞).
2.Функция является функцией общего вида в смысле четности и нечетности.
3.Точки пересечения с координатными осями: c осью Оу: x = 0; y = 1;
сосью Ох: y = 0; x = 1;
4.Точки разрыва и асимптоты: Вертикальных асимптот нет.
Наклонные асимптоты: общее уравнение y = kx + b;
k = lim |
|
f (x) |
|
|
|
|
3 1− x3 |
|
|
1− x3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
= lim |
|
|
|
|
|
= lim 3 |
|
|
= lim |
3 |
|
|
|
−1 = −1; |
|
|
|
|
|
|
||||||||
|
x |
|
|
x |
|
|
|
x3 |
|
x3 |
|
|
|
|
|
|
|||||||||||||||
x→∞ |
|
|
x→∞ |
|
|
|
|
x→∞ |
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
||||||||||
b = lim( f (x) − kx) |
= lim(3 |
1− x3 + x) = lim |
|
|
|
|
|
(1− x3 + x3 ) |
|
|
|
|
= 0; |
||||||||||||||||||
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||
x→∞ |
|
|
|
|
|
|
x→∞ |
|
|
|
|
x←∞ |
|
|
3 |
3 |
1 |
− x |
3 |
+ x |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1− x |
|
|
) − x |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итого: у = -х – наклонная асимптота. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
5. Возрастание и убывание функции, точки экстремума. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
1 |
|
|
|
3 |
|
−2 / 3 |
|
(−3x |
2 |
). Видно, что у′< 0 при любом х ≠ 0, следовательно, функция |
|||||||||||||||||||||
y′ = |
|
(1 |
− x |
|
) |
|
|
|
|||||||||||||||||||||||
3 |
|
|
|
||||||||||||||||||||||||||||
убывает на всей области определения и не имеет экстремумов. В точке х = 0 первая производная функции равна нулю, однако в этой точке убывание не сменяется на возрастание, следовательно, в точке х = 0 функция скорее всего имеет перегиб. Для нахождения точек перегиба, находим вторую производную функции.
y′′ = |
|
− 2x |
y′′ = 0 при х =0 и y′′ = ∞ при х = 1. |
|
(1− x3 )5 |
||
3 |
|
||
Точки (0,1) и (1,0) являются точками перегиба, т.к. y′′(1-h) < 0; y′′(1+h) >0; y′′(-h) > 0; y′′(h) < 0 для любого h > 0.
6. Построим график функции.
51

|
|
|
|
Ларин Александр Александрович “Курс высшей математики. Часть 2.” |
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
-2 |
|
-1 |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
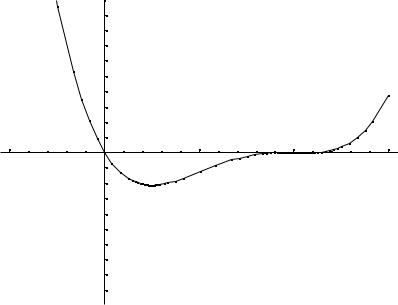
Пример: Исследовать функцию |
y = |
x3 |
+ 4 |
и построить ее график. |
||||||||||
|
x2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. Областью определения функции являются все значения х, кроме х = 0. |
||||||||||||||
2. Функция является функцией общего вида в смысле четности и нечетности. |
||||||||||||||
3. Точки пересечения с координатными осями: c осью Ох: y = 0; x = − 3 4 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
с осью Оу: x = 0; y – не существует. |
||
4. Точка х = 0 является точкой разрыва lim y = ∞, следовательно, прямая х = 0 является |
||||||||||||||
вертикальной асимптотой. |
|
|
|
x→0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
Наклонные асимптоты ищем в виде: y = kx + b. |
|
|
|
|||||||||||
k = lim |
f (x) |
= lim |
x3 + 4 |
|
+ |
4 |
|
=1 |
|
|
|
|
|
|
x |
x3 |
= lim 1 |
x3 |
|
|
|
|
|
|
|
||||
x→∞ |
x→∞ |
x→∞ |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
3 |
+ 4 |
|
|
4 |
|
||||
|
|
|
|
|
|
|
x |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
= lim |
3 |
= 0. |
||||
b = lim( f (x) − kx) = lim |
x |
− x |
||||||||||||||
|
|
x→∞ |
x→∞ |
|
|
x→∞ x |
|
|
||||||||
Наклонная асимптота у = х. |
|
|
|
|
|
|||||||||||
5. Находим точки экстремума функции. |
|
|
||||||||||||||
y |
′ |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
− x3 ; |
y′ = 0 при х = 2, у′ = ∞ при х = 0. |
||||||||||||||
|
||||||||||||||||
y′ > 0 при х (-∞, 0) – функция возрастает, y′ < 0 при х (0, 2) – функция убывает, у′ > 0 при х (2, ∞) – функция возрастает.
Таким образом, точка (2, 3) является точкой минимума.
Для определения характера выпуклости/вогнутости функции находим вторую производную.
y′′ = 24x4 > 0 при любом х ≠ 0, следовательно, функция, вогнутая на всей области определения.
6. Построим график функции.
52
Ларин Александр Александрович “Курс высшей математики. Часть 2.” |
|||
|
8 |
|
|
|
6 |
|
|
|
4 |
|
|
|
2 |
|
|
-4 |
-2 |
2 |
4 |
|
-2 |
|
|
|
-4 |
|
|
Пример: Исследовать функцию y = x(x −1)3 |
и построить ее график. |
||
1.Областью определения данной функции является промежуток х (-∞, ∞).
2.В смысле четности и нечетности функция является функцией общего вида.
3.Точки пересечения с осями координат: с осью Оу: x = 0, y = 0;
сосью Ох: y = 0, x = 0, x = 1.
4.Асимптоты кривой.
Вертикальных асимптот нет.
Попробуем найти наклонные асимптоты в виде y = kx + b.
k = lim |
f (x) |
= lim |
x(x −1) |
3 |
= ∞ |
- наклонных асимптот не существует. |
x |
x |
|
||||
x→∞ |
x→∞ |
|
|
|
5. Находим точки экстремума.
y′ = [x(x3 −3x2 + 3x −1]′ = [x4 −3x3 + 3x2 − x]′ = 4x3 −9x2 + 6x −1
Для нахождения критических точек следует решить уравнение 4х3 – 9х2 +6х –1 = 0. Для этого разложим данный многочлен третьей степени на множители.
Подбором можно определить, что одним из корней этого уравнения является число х = 1. Тогда:
4x3 – 9x2 + 6x – 1 x - 1 |
|
4x3 – 4x2 |
4x2 – 5x + 1 |
-5x2 + 6x
- 5x2 + 5x
x- 1
x - 1 0
Тогда можно записать (х – 1)(4х2 – 5х + 1) = 0. Окончательно получаем две критические точки: x = 1 и x = ¼.
Примечание. Операции деления многочленов можно было избежать, если при нахождении производной воспользоваться формулой производной произведения:
y′ = [x(x −1)3 ]′ = (x −1)3 + 3x(x −1)2 = (x −1)2 (x −1+ 3x) = (x −1)2 (4x −1)
53
Ларин Александр Александрович “Курс высшей математики. Часть 2.”
Найдем вторую производную функции: 12x2 – 18x + 6. Приравнивая к нулю, находим: x = 1, x = ½.
Систематизируем полученную информацию в таблице:
|
(-∞ ; ¼) |
1/4 |
( ¼ ; ½) |
1/2 |
( ½ ; 1 ) |
1 |
(1 ; ∞) |
f′′(x) |
+ |
+ |
+ |
0 |
- |
0 |
+ |
f′(x) |
- |
0 |
+ |
+ |
+ |
0 |
+ |
f(x) |
убывает |
min |
возрастает |
пере |
возрастает |
пере |
возрастает |
|
вып.вниз |
|
вып.вниз |
гиб |
вып.вверх |
гиб |
вып. вниз |
6. Построим график функции.
0.4
0.2
-0.5 |
0.5 |
1 |
1.5 |
||
|
|
|
|
|
|
|
|
|
|
|
|
-0.2
-0.4
Интегральное исчисление.
Первообразная функция.
Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:
F′(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) = F2(x) + C.
Неопределенный интеграл.
54

Ларин Александр Александрович “Курс высшей математики. Часть 2.”
Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: ∫ f (x)dx = F(x) +C;
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
1.(∫ f (x)dx)′ = (F(x) + C)′ = f (x);
2.d (∫ f (x)dx)= f (x)dx;
3.∫dF(x) = F(x) +C;
4.∫(u + v − w)dx = ∫udx + ∫vdx − ∫wdx; где u, v, w – некоторые функции от х.
6. ∫C f (x)dx = C ∫ f (x)dx;
Пример: ∫(x2 − 2sin x +1)dx = ∫x2 dx − 2∫sin xdx + ∫dx = 13 x3 + 2cos x + x + C;
Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача. Ниже будут рассмотрены способы нахождения неопределенных интегралов для основных классов функций – рациональных, иррациональных, тригонометрических, показательных и др.
Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друг друга, поэтому ниже приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.
|
Интеграл |
|
|
|
|
|
|
Значение |
|
Интеграл |
|||||||||||||||||||||||||
1 |
∫tgxdx |
|
|
|
|
|
-ln cosx +C |
9 |
∫ex dx |
|
|
|
|
|
|||||||||||||||||||||
2 |
∫ctgxdx |
|
|
|
|
|
|
|
|
ln sinx + C |
10 |
∫cos xdx |
|||||||||||||||||||||||
3 |
∫a x dx |
|
|
|
|
|
|
|
|
|
|
|
|
a x |
|
|
|
|
|
|
|
11 |
∫sin xdx |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ C |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln a |
|
|
|
|
|
|
|
|
|
|
|||||||||
4 |
∫ |
|
|
dx |
|
|
|
|
|
1 |
arctg |
x |
+ C |
12 |
∫ |
1 |
|
|
|
dx |
|||||||||||||||
|
a |
2 |
+ x |
2 |
|
|
|
|
|
|
|
a |
a |
|
|
cos |
2 |
x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5 |
|
|
|
dx |
|
|
|
|
1 |
|
|
|
|
|
x + a |
|
|
|
|
|
13 |
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
∫ |
|
|
|
|
|
|
|
ln |
|
|
|
|
+ C |
|
∫ |
|
dx |
|||||||||||||||||
|
x2 |
− a2 |
|
|
|
|
|
|
|
sin 2 x |
|||||||||||||||||||||||||
|
|
|
|
|
2a |
x − a |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
6 |
∫ |
|
|
dx |
|
|
|
|
ln |
|
x + x2 ± a2 |
|
+C |
14 |
∫ |
|
|
dx |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
x2 ± a2 |
|
|
a2 − x2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Значение ex + C
sinx + C -cosx + C
tgx + C
-ctgx + C
arcsin ax + C
55

|
|
|
|
|
Ларин Александр Александрович “Курс высшей математики. Часть 2.” |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7 |
∫ |
xαdx |
|
xα+1 |
|
|
|
|
|
15 |
1 |
|
dx |
|
x |
|
π |
|
|||||||
|
|
|
|
|
|
+C,α ≠ −1 |
|
|
|
|
|
ln |
tg |
|
|
+ |
|
|
+C |
||||||
|
|
|
|
|
|
|
∫cos x |
|
|
|
|||||||||||||||
|
|
|
|
α +1 |
|
2 |
|
4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8 |
|
dx |
|
|
|
ln |
|
x |
|
+ C |
16 |
1 |
|
|
|
|
|
|
|
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∫ |
|
|
|
|
|
|
|
|
|
|
∫ |
|
dx |
|
ln |
tg |
|
+C |
||||||
|
x |
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Методы интегрирования.
Рассмотрим три основных метода интегрирования.
Непосредственное интегрирование.
Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным
инструментом проверки результатов интегрирования. |
|
|
|
||||||||||||
Рассмотрим применение этого метода на примере: |
|
|
|||||||||||||
Требуется |
найти |
значение интеграла ∫ |
dx |
. На |
основе |
известной |
формулы |
||||||||
x |
|||||||||||||||
|
|
|
|
|
(ln x)′ = |
1 |
|
|
|
|
|
|
|||
дифференцирования |
|
можно сделать вывод, |
что искомый интеграл равен |
||||||||||||
x |
|||||||||||||||
ln x + C , |
где |
С |
– |
некоторое |
постоянное |
число. |
Однако, |
с другой |
стороны |
||||||
′ |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
||
(ln(−x)) = − |
|
(−1) |
= |
|
. Таким образом, окончательно можно сделать вывод: |
|
|||||||||
x |
x |
|
|||||||||||||
∫dxx = ln x +C
Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.
Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.
Способ подстановки (замены переменных).
Теорема: Если требуется найти интеграл ∫ f (x)dx , но сложно отыскать
первообразную, то с помощью замены x = ϕ(t) и dx = ϕ′(t)dt получается:
∫ f (x)dx = ∫ f (ϕ(t))ϕ′(t)dt
Доказательство: Продифференцируем предлагаемое равенство: d ∫ f (x)dx = d (∫ f [ϕ(t)]ϕ′(t)dt)
56

Ларин Александр Александрович “Курс высшей математики. Часть 2.”
По рассмотренному выше свойству №2 неопределенного интеграла: f(x)dx = f[ϕ(t)]ϕ′(t)dt
что с учетом введенных обозначений и является исходным предположением. Теорема доказана.
Пример. Найти неопределенный интеграл ∫ sin x cos xdx .
sin x cos xdx .
Сделаем замену t = sinx, dt = cosxdt. |
|
|
|
|
||||||||||||||
∫ tdt = ∫t1/ 2 dt = |
2 |
t 3 / 2 |
+ C = |
2 |
sin3 / 2 |
x + C. |
|
|
||||||||||
3 |
3 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример. ∫x(x2 |
+1)3 / 2 dx. |
dt |
|
|
|
|
|||||||||||
Замена t = x2 +1; |
|
dt = 2xdx; |
|
dx = |
; Получаем: |
|
||||||||||||
|
|
2x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫t 3 / 2 |
dt |
= |
1 |
∫t 3 / 2 dt = |
1 |
|
2 |
t 5 / 2 |
+ C = |
t 5 / 2 |
+ C = |
(x2 +1)5 / 2 |
+ C; |
|||||
|
|
|
|
|
5 |
|||||||||||||
2 |
2 |
|
2 |
5 |
|
|
|
|
5 |
|
|
|
||||||
Ниже будут рассмотрены другие примеры применения метода подстановки для различных типов функций.
Интегрирование по частям.
Способ основан на известной формуле производной произведения: (uv)′ = u′v + v′u
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем: ∫d(uv) = ∫udv + ∫vdu , а в соответствии с приведенными выше свойствами неопределенного интеграла:
uv = ∫udv + ∫vdu |
или |
∫udv = uv − ∫vdu ; |
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример. ∫x2 |
|
2 |
; dv = sin xdx; |
|
= −x2 cos x + ∫cos x 2xdx = |
|
sin xdx = u = x |
|
|
||||
|
du = 2xdx; |
v = −cos x |
|
|||
u = x; |
dv = cos xdx; |
= −x2 |
cos x + 2[x sin x − ∫sin xdx]= −x2 cos x + 2x sin x + 2cos x +C. |
|
= |
|
|
||
du = dx; v = sin x |
|
|
|
|
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
|
2 x |
; du |
= 2e |
2x |
dx; |
|
= e2 x sin x − ∫sin x 2e2x dx = |
Пример. ∫e2 x cos xdx = u = e |
|
|
|
||||
dv = cos xdx; |
v = sin x |
|
|||||
57

|
|
|
|
|
|
Ларин Александр Александрович “Курс высшей математики. Часть 2.” |
|
|
2 x |
; du |
= 2e |
2 x |
dx; |
|
= e2 x sin x − 2[− e2 x cos x − ∫− cos x 2e2 x dx]= e2x sin x + |
= u = e |
|
|
|
||||
dv = sin xdx; |
v = −cos x; |
|
|||||
+ 2e2 x cos x − 4∫cos xe2 x dx
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.
5∫e2 x cos xdx = e2 x (sin x + 2cos x)
∫e2 x cos xdx = e2 x
5
Таким образом, интеграл найден вообще без применения таблиц интегралов.
Прежде чем рассмотреть подробно методы интегрирования различных классов функций, приведем еще несколько примеров нахождения неопределенных интегралов приведением их к табличным.
|
|
|
|
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∫(2x +1)20 dx = {2x +1 = t; |
|
|
|
dt = 2dx;}= ∫t 20 |
|
1 |
dt = |
|
|
1 |
|
|
t 21 |
1 |
+C = |
t 21 |
|
|
+ C = |
(2x +1)21 |
+ C |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
21 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
42 |
|
|
|
|
|
|
|
|
|
|
|
|
42 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∫ |
|
|
2 − x2 |
+ 2 + x2 |
dx = ∫ |
|
|
2 − x2 + 2 + x |
2 |
|
|
dx = ∫ |
|
|
|
|
dx |
|
|
|
|
+ ∫ |
|
|
|
dx |
|
|
|
|
= ln |
|
x + x |
2 |
+ 2 |
|
+ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
− x |
4 |
|
|
|
|
|
|
|
|
|
|
|
2 − x |
2 |
|
2 |
+ x |
2 |
|
|
|
|
|
|
2 + x |
2 |
|
|
|
2 − x |
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
+ arcsin |
x |
+C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∫ |
|
|
cos x |
|
dx = |
∫sin − 3 / 2 |
|
|
x cos xdx = {sin x = t; |
|
|
|
dt |
|
= cos xdx} = ∫t − 3 / 2 dt |
= −2t − 1 / 2 + C = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
sin 3 x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= −2sin −1/ 2 x + C = − |
|
|
|
|
|
|
+ C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
; |
|
|
dv = e |
5x |
dx; |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2e |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x |
2 |
e |
5x |
dx |
|
|
u = x |
|
|
|
|
|
|
|
|
|
|
|
e |
5x |
x |
2 |
|
|
|
|
|
|
e |
5x |
2xdx |
|
|
|
5x |
|
|
|
xe |
5x |
dx |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x |
|
= |
|
|
|
|
|
− |
|
|
|
|
|
|
|
= |
|
|
|
|
|
− |
|
|
|
|
|
|
= |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
5 |
|
|
|
∫5 |
|
|
|
5 |
|
|
5 |
|
|
∫ |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
du |
= 2xdx; |
v = |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
dv = e |
5x |
dx; |
|
|
|
|
|
x |
2e5x |
|
|
|
|
2 |
xe5x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2e5x |
|
2xe5x |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
u = x; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− ∫ |
|
|
5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
∫e |
5x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
dx |
= |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
+ |
|
|
|
|
dx |
= |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x |
|
|
|
|
5 |
|
|
|
5 |
|
|
5 |
|
5 |
|
|
|
|
5 |
|
25 |
|
|
|
25 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
du = dx; v = |
|
|
|
|
e |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
2e |
5x |
|
2xe5x |
|
|
|
2e5x |
|
|
|
e5x |
|
2 |
|
|
|
2x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
− |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
x |
|
|
|
− |
|
|
|
|
+ |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
5 |
|
|
|
25 |
125 |
|
|
|
5 |
|
|
|
|
|
5 |
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
58
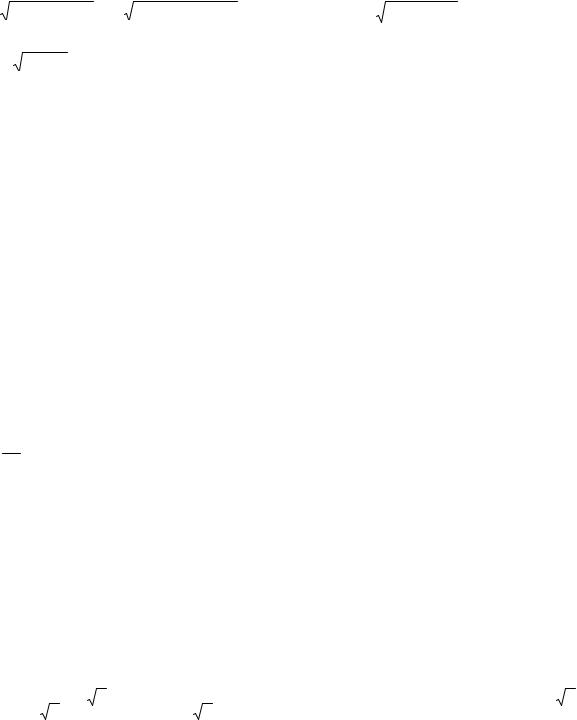
Ларин Александр Александрович “Курс высшей математики. Часть 2.”
Пример.
∫ |
|
|
|
|
|
dx |
|
|
|
|
|
= ∫ |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
= {dx = d (x +1)}= ∫ |
|
d (x +1) |
|
|
|
= {x +1 = t}= |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
− x |
2 |
|
|
|
|
|
|
|
|
− x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 − (x +1) |
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
− 2x +8 |
|
|
|
|
|
|
|
− 2x −1+ 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
= ∫ |
|
|
|
dt |
|
|
|
= arcsin |
t |
|
+ C = arcsin |
x +1 |
+ C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
3 |
2 |
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
−t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ln x |
|
|
|
|
|
u = ln x; |
|
dv = |
|
|
|
dx; |
|
|
|
|
|
ln x |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
ln x |
|
|
1 dx |
|
|
|
ln x |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
|
− |
|
|
− |
|
|
|
|
|
|
|
|
dx = − |
|
|
|
+ |
|
|
|
|
|
|
= − |
|
|
|
+ |
|
|||||||||||||||||
∫ x3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2x2 |
∫ |
2x2 |
|
x |
2x2 |
|
2 ∫ x3 |
2x2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
du = |
|
|
|
|
dx; |
|
v = − |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
2x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
1 |
|
|
−2 |
|
|
|
|
|
|
|
|
|
ln x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
+ |
|
|
− |
|
|
|
x |
|
|
+C |
= − |
|
|
|
|
|
− |
|
|
|
|
|
|
|
+C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
2 |
|
|
|
|
2x |
2 |
4x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
u = ln x; |
|
|
|
dv = xdx; |
|
|
|
x2 |
|
|
|
|
|
|
x2 |
|
|
1 |
|
|
|
|
|
x2 |
ln x |
|
1 |
|
|
|
|
|
|
|
x2 |
ln x |
|
|
|
x2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x ln xdx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
= |
|
|
|
|
ln x |
− |
|
|
|
|
|
|
|
|
|
dx = |
|
|
|
|
− |
|
|
|
|
xdx = |
|
|
|
|
− |
|
|
+ C = |
|||||||||||||||||||||
∫ |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
2 |
|
∫ 2 |
|
|
x |
|
|
2 |
|
2 ∫ |
|
|
|
2 |
|
4 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
du |
= |
dx; v |
= |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
=x2 (2ln x −1) + C. 4
Пример.
∫ecos2 x sin 2xdx = {t = ecos2 x ; dt = −ecos2 x 2cos x sin x = −sin 2x ecos2 x dx;}= −∫dt = −t +C = = −ecos2 x + C.
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∫ |
dx |
|
|
x = t; |
dt |
|
|
1 |
|
1 |
|
= ∫ |
|
2tdt |
= 2∫ |
|
dt |
= 2arctgt +C = 2arctg x + C. |
|||
|
|
= |
|
= |
|
|
= |
|
|
|
|
|
|
|
|
|
|||||
(x +1) |
x |
dx |
|
x |
|
(t |
2 |
+1)t |
t |
2 |
+1 |
||||||||||
|
|
|
2 |
|
2t |
|
|
|
|
|
|||||||||||
Пример.
∫ |
|
|
dx |
= ∫ |
dx |
|
|
1 |
∫ |
|
dx |
|
|
|
1 |
x −3 |
|
|
|||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= |
|
|
arctg |
|
|
+C. |
|||
x |
2 |
−6x + 25 |
(x −3) |
2 |
+16 |
16 |
x −3 |
|
2 |
|
16 |
4 |
|||||||||||
|
|
|
|
|
|
|
+1 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
59

Ларин Александр Александрович “Курс высшей математики. Часть 2.”
Интегрирование элементарных дробей.
Определение: Элементарными называются дроби следующих четырех типов:
I. |
1 |
; |
|
III. |
|
Mx + N |
; |
ax +b |
|
|
ax2 + bx + c |
||||
II. |
1 |
|
; |
IV. |
|
Mx + N |
|
(ax +b)m |
(ax2 + bx + c)n |
||||||
m, n – натуральные числа (m ≥ 2, n ≥ 2) и b2 – 4ac <0.
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.
I. |
∫ |
dx |
= |
|
1 |
|
∫ |
dt |
= |
|
1 |
ln |
|
t |
|
+ C = |
1 |
ln |
|
|
ax + b |
|
+ C. |
|
|
|||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
ax +b |
|
|
|
a |
|
|
|
t |
|
|
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
II. |
∫ |
|
dx |
|
|
= |
1 |
∫ |
dt |
|
= − |
1 |
|
|
+ C = − |
1 |
|
+ C; |
||||||||||||||
(ax + b) |
m |
|
|
a |
m |
a(m −1)t |
m−1 |
a(m −1)(ax + b) |
m−1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Рассмотрим метод интегрирования элементарных дробей вида III. Интеграл дроби вида III может быть представлен в виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
Ap |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Ax + B |
|
|
|
|
|
|
|
(2x + p) + |
B |
− |
|
|
|
|
|
|
|
A |
|
|
|
|
|
2x + p |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
∫ |
|
|
|
|
|
= ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
|
dx + B − |
|||||||
x |
2 |
+ px + q |
|
|
|
|
x |
2 |
+ px + q |
|
|
|
|
|
2 |
|
x |
2 |
+ px + q |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
A |
|
|
2 |
|
|
|
|
|
|
|
|
|
Ap |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
A |
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= |
|
|
|
ln |
x |
|
+ px |
+ q |
+ |
B − |
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
ln |
x |
|
+ px + q |
+ |
||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
+ q − |
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
arctg |
2x + p |
|
+C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
4q − p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ap |
|
|
dx |
|
|
|
∫ |
|
|
|
= |
2 |
x |
2 |
+ px + q |
||
|
|
|
|||
2B − Ap
4q − p2
Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.
Рассмотрим применение указанной выше формулы на примерах.
Пример.
60
