
Высшая матматика том2
.pdf
Ларин Александр Александрович “Курс высшей математики. Часть 2.”
y y = ψ(x)
y = ϕ(x)
a |
b |
x |
Пример. Вычислить интеграл ∫∫(x − y)dxdy , если область |
ограничена |
линиями: y = 0, y = x2, x = 2. |
|
y |
|
4 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
x2 |
2 |
|
2 |
|
|
y=x |
2 |
2 |
|
|
|
4 |
|
|
4 |
|
|
5 |
2 |
|
|||
∫∫ f (x, y)dxdy = ∫dx ∫ |
(x − y)dy = ∫(xy − |
y |
|
|
|
|
|
|
= ∫(x |
3 |
|
x |
|
x |
|
|
x |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
) |
|
|
|
|
− |
|
|
)dx = |
|
|
− |
|
|
|
|
|
= |
||||
2 |
|
|
|
|
|
2 |
4 |
10 |
||||||||||||||||
0 |
0 |
0 |
|
|
y=0 |
0 |
|
|
|
|
0 |
|
||||||||||||
= 4 −3,2 = 0,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема. Если функция f(x, y) непрерывна в замкнутой области ,
ограниченной линиями y = c, y = d (c < d), x = Φ(y), x = Ψ(y) (Φ(y) ≤ Ψ(y)), то
|
d |
Ψ( y) |
|
|
∫∫ f (x, y)dxdy = ∫dy ∫ f (x, y)dx |
|
|||
|
c Φ( y) |
|
||
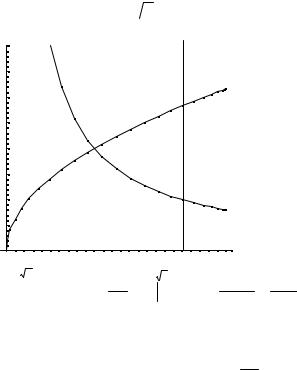
Пример. Вычислить интеграл ∫∫(x2 |
+ y2 )dxdy , если область |
ограничена |
||
линиями y = x, x = 0, y = 1, y = 2. |
|
|
|
|
y |
|
|
|
|
2 |
|
y = x |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0 |
|
|
x |
|
111
Ларин Александр Александрович “Курс высшей математики. Часть 2.”
|
2 |
|
2 |
|
2 |
x |
|
2 |
|
|
2 |
|
|
2 |
x3 |
|
|
|
|
2 |
|
|
|
|
y |
|
|
2 |
4 |
|
3 |
|
|
4 |
|
|
4 |
|
|
2 |
|
64 |
|
4 |
|
|||||
∫∫(x |
|
)dxdy = ∫dy∫(x |
|
|
)dx = ∫ |
|
|
|
|
|
|
|
|
dy = ∫ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
+ y |
|
|
+ y |
|
|
|
|
|
+ y |
|
x |
|
|
|
|
y |
|
|
dy = |
|
|
|
y |
|
|
|
|
= |
|
− |
|
= 5 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
12 12 |
|
|||
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Пример. |
|
Вычислить |
интеграл |
|
|
∫∫(3x2 |
− 2xy + y)dxdy , |
|
|
если |
область |
||||||||||||||||||||||||||||||||||||||
интегрирования |
ограничена линиями х = 0, х = у2, у = 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|||
|
|
∫∫(3x2 |
− 2xy + y)dxdy = ∫dy ∫(3x2 |
− 2xy + y)dx = ∫(x3 − yx2 |
|
+ yx) |
|
|
|
dy = |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
y |
7 |
|
|
|
y |
6 |
|
|
y |
4 |
|
2 |
|
244 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
= ∫( y |
6 |
|
5 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
− y |
|
|
+ y |
|
)dy = |
|
|
|
|
− |
|
|
|
|
+ |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
7 |
|
6 |
|
4 |
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Пример. |
Вычислить |
|
|
двойной |
|
|
интеграл |
|
|
∫∫y ln xdxdy , |
|
|
если |
область |
|||||||||||||||||||||||||||||||||||
интегрирования ограничена линиями ху=1, у =  x , х = 2.
x , х = 2.
2 |
|
|
|
|
|
|
|
|
1.75 |
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
1.25 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0.75 |
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
0.25 |
|
|
|
|
|
|
|
|
|
0.5 |
1 |
|
1.5 |
2 |
|
2.5 |
|
2 |
x |
2 |
y2 |
x |
2 |
x ln x |
|
|
∫∫y ln xdxdy = ∫dx ∫y ln xdy = ∫ |
2 |
ln x |
dx = ∫ |
2 |
− |
|||
1 |
1/ x |
1 |
1/ x |
1 |
|
|
||
ln x
2x2 dx
|
|
|
|
u = ln x; dv |
= xdx; |
|
|
x2 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1. |
|
|
x ln xdx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
= |
|
|
|
ln x − |
|
|
|
|
dx = |
|
|
|
ln x − |
|||||||||
∫ |
|
|
|
|
1 |
|
|
|
|
|
|
x |
2 |
|
∫2 |
2 |
|
||||||||||||||||||||||||
|
|
du = |
dx; v = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
2 |
|
|
|
|
x |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||
|
|
|
|
|
x |
|
ln x − |
|
|
= 2ln 2 −1+ |
|
= 2ln 2 − |
. |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
∫x ln xdx = |
2 |
4 |
|
4 |
|
4 |
|
|
||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
ln x |
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
txdt |
|
|
|
|
tdt |
|
|
|
|
|
|
|
|
|
u = t; |
||||||||
|
|
ln x = t; |
|
x = e |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
−t |
|
|
|
|||||||||||||||||||
2. |
|
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
|
|
|
|
|
= |
|
|
e |
|
tdt |
= |
|
||||||
∫ x2 |
|
|
1 |
|
|
|
|
|
|
|
∫ |
x2 |
∫ |
x |
|
∫ |
|
|
|||||||||||||||||||||||
|
dt |
= |
dx; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dv = e |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 ; 4
du = dt; |
|
= −te−t + |
|
|
|
−t dt; v = −e−t ; |
|
|
112

|
|
|
|
|
|
|
|
|
|
|
|
|
Ларин Александр Александрович “Курс высшей математики. Часть 2.” |
||||||||||||||||||||||||||
+ ∫e−t dt = −te−t −e−t = − |
ln x |
|
− |
1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
ln x |
|
ln x |
|
|
|
1 |
|
2 |
|
|
|
ln 2 |
|
1 |
|
|
|
|
ln 2 |
|
1 |
|
|
|
|
|
|
|
|
|||||||||
∫ |
|
|
dx = − |
|
|
− |
|
|
|
|
= − |
|
|
|
|
|
− |
|
|
+1 = − |
|
|
|
+ |
|
; |
|
|
|
|
|
|
|
||||||
x |
2 |
x |
|
|
x |
|
2 |
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
||||||||||||||||||
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
∫∫y ln xdxdy = |
1 |
|
|
|
|
|
|
3 |
|
|
ln 2 |
|
|
1 |
1 5ln 2 |
|
5 |
|
5ln 2 |
|
5 |
|
||||||||||||||||
3. |
|
|
2ln 2 − |
|
|
+ |
|
|
|
|
|
− |
|
= |
|
|
|
|
|
|
− |
|
|
= |
|
− |
|
. |
|||||||||||
2 |
4 |
|
|
|
2 |
|
|
2 |
|
2 |
|
|
4 |
8 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
||||||||||||||
При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая вычисляет двойной интеграл от любой функции.
Для запуска программы дважды щелкните на значке
Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (© Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.
Замена переменных в двойном интеграле.
Расмотрим двойной интеграл вида ∫∫F(x, y)dydx , где переменная х изменяется в
пределах от a до b, а переменная у – от ϕ1(x) до Положим х = f(u, v); y = ϕ(u, v)
Тогда dx = |
∂f |
du + |
∂f |
dv ; |
dy = |
∂ϕ du + |
∂ϕ dv ; |
|
∂u |
|
∂v |
|
|
∂u |
∂v |
∫∫F(x, y)dydx = ∫b dx
a
ϕ2(х).
ϕ2 ( x)
∫F(x, y)dy
ϕ1 ( x)
т.к. при первом интегрировании переменная х принимается за постоянную, то dx = 0.
∂∂uf du + ∂∂fv dv = 0 , т.е. du = − ∂∂ff  ∂∂uv dv
∂∂uv dv
пожставляя это выражение в записанное выше соотношение для dy, получаем:
|
∂ϕ |
|
∂f ∂v |
|
∂ϕ dv = |
∂ϕ |
|
∂f |
− |
∂ϕ |
∂f |
|
dy = − |
|
dv + |
∂v |
|
∂u |
|
∂u |
∂v |
dv |
|||
∂u |
|
|
|
|
∂f |
|
|
|||||
|
|
∂f ∂u |
∂v |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
∂u |
|
|
|
113
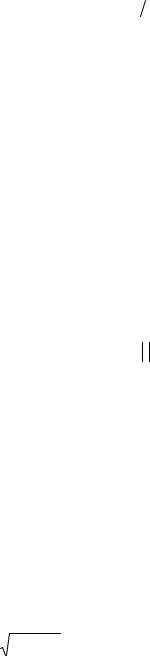
|
|
|
|
|
Ларин Александр Александрович “Курс высшей математики. Часть 2.” |
||||||||||
|
∂ϕ |
|
∂f |
|
∂ϕ |
|
∂f |
|
∂f |
∂f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Выражение |
|
− |
|
= |
∂u |
∂v |
= |
|
i |
|
называется определителем Якоби или |
||||
|
|
||||||||||||||
∂v |
∂u |
∂u |
∂v |
∂ϕ ∂ϕ |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
∂u |
∂v |
|
|
|
|
|
Якобианом функций f(u, v) и ϕ(u, v).
(Якоби Карл Густав Якоб – (1804-1851) – немецкий математик)
Тогда ∫∫F(x, y)dydx = ∫b dx |
Ψ ( x) |
|
|
i |
|
|
|
|
|
|
|||
2∫ |
F( f (x, y),ϕ(x, y)) |
|
|
dv |
||
|
|
|
||||
∂f |
|
du |
||||
a |
Ψ1 ( x) |
|
|
|
||
|
|
|
|
|
||
Т.к. при первом интегрировании приведенное |
|
выше выражение для dx |
||||
принимает вид dx = |
∂f |
du ( при первом интегрировании полагаем v = const, dv = 0), то |
|||||
|
∂u |
|
|
|
|
|
|
при изменении порядка интегрирования, получаем соотношение: |
|||||||
|
|
V2 |
Θ2 (v) |
||||
|
∫∫F(x, y)dydx = ∫dv |
∫F( f (u,v),ϕ(u,v)) |
|
i |
|
du |
|
|
|
|
|||||
|
|
|
|||||
|
|
V1 |
Θ1 (v) |
||||
Двойной интеграл в полярных координатах.
Воспользуемся формулой замены переменных:
∫∫F (x, y)dxdy = ∫∫F( f (u,v),ϕ(u,v)) i dudv
x = ρcosθ
При этом известно, что
y = ρsin θ
В этом случае Якобиан имеет вид:
|
|
|
|
∂x |
|
∂x |
|
cos θ |
−ρsin θ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
i |
|
= |
∂ρ |
|
∂θ |
= |
= ρcos |
2 |
θ+ρsin θ = ρ |
||
|
|
|||||||||||
|
|
∂y |
|
∂y |
sin θ |
ρcos θ |
|
|||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
∂ρ |
|
∂θ |
|
|
|
|
|
|
Тогда ∫∫F(x, y)dxdy = ∫∫F(ρcos θ,ρsin θ)ρdρdθ = ∫∫ f (ρ,θ)ρdρdθ
τ |
τ |
|
|
|
Здесь τ - новая область значений, ρ = x2 + y2 ; |
θ = arctg |
y |
; |
|
x |
||||
|
|
|
114

Ларин Александр Александрович “Курс высшей математики. Часть 2.”
Тройной интеграл.
При рассмотрении тройного инеграла не будем подробно останавливаться на всех тех теоретических выкладках, которые были детально разобраны применительно к двойному интегралу, т.к. существенных различий между ними нет.
Единственное отличие заключается в том, что при нахождении тройного интеграла интегрирование ведется не по двум, а по трем переменным, а областью интегрирования является не часть плоскости, а некоторая область в техмерном пространстве.
∫∫∫f (x, y, z)dxdydz = limx→0 |
∑∑∑ f (x, y, z) x y z |
|
r |
y→0 |
v |
|
z→0 |
|
Суммирование производится по области v, которая ограничена некоторой поверхностью ϕ(x, y, z) = 0.
|
x2 |
y2 |
z2 |
|
∫∫∫f (x, y, z)dxdydz = ∫∫∫ |
f (x, y, z)dzdydx |
|||
r |
x1 |
y1 |
z1 |
|
Здесь х1 и х2 – постоянные величины, у1 и у2 – могут быть некоторыми функциями от х или постоянными величинами, z1 и z2 – могут быть функциями от х и у или постоянными величинами.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x2 xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Пример. |
Вычислить интеграл ∫∫∫x2 yzdzdydx |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 x2 xy |
2 |
|
|
|
1 x2 |
2 |
z 2 |
|
xy |
|
|
|
1 1 x2 |
2 |
2 2 |
1 1 x2 |
4 3 |
1 1 |
4 |
|
y 4 |
|
|
x2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
∫∫∫x yzdzdydx = ∫∫x |
|
|
|
|
|
|
|
|
|
|
|
|
∫∫x |
|
yx y dydx = |
|
∫∫x |
y dydx = |
|
∫x |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
y |
|
|
|
|
dydx = |
|
|
|
|
|
|
|
|
|
|
dx = |
|||||||||||||||||||
0 0 0 |
|
|
|
|
0 0 |
|
|
2 |
|
0 |
|
|
|
2 0 0 |
|
|
2 |
0 0 |
|
2 |
0 |
|
|
4 |
|
|
0 |
|||||||||
= |
1 |
∫1 |
x4 x8 |
dx = |
1 |
∫1 x12 dx = |
|
1 |
|
1 |
|
x13 |
|
1 = |
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2 |
0 |
|
4 |
|
8 |
0 |
|
|
8 |
|
13 |
|
|
|
0 |
104 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Замена переменных в тройном интеграле.
Операция замены переменных в тройном интеграле аналогична соответсвующей операции для двойного интеграла.
Можно записать:
∫∫∫F(x, y, z)dxdydz = ∫∫∫F( f (u,v, w),ϕ(u,v, w),ψ(u,v, w)) i dudvdw
r τ
115
Ларин Александр Александрович “Курс высшей математики. Часть 2.”
|
|
|
|
∂x |
∂x |
∂x |
|
|
|
|
|
|
|||
|
|
|
|
∂u |
∂v |
∂w |
|
|
i |
|
= |
∂y |
∂y |
∂y |
|
|
|
|
|||||
|
|
∂u |
∂v |
∂w |
|
||
|
|
|
|
|
|||
|
|
|
|
∂z |
∂z |
∂z |
|
|
|
|
|
∂u |
∂v |
∂w |
|
Наиболее часто к замене переменной в тройном интеграле прибегают с целью перейти от декартовой прямоугольной системы координат к цилиндрической или сферической системе. См. Цилиндрическая и сферическая системы координат.
Рассмотрим эти преобразования подробнее.
Цилиндрическая система координат.
z
P
z
0
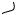 θ x
θ x
ρ
y
Связь координат произвольной точки Р пространства в цилиндрической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:
x = ρcos θy = ρsin θ
z = z
|
|
|
|
|
|
ρ = |
x2 + y2 ; |
θ = arctg |
y |
; |
z = z; |
|||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||
Для представления тройного интеграла в цилиндрических координатах |
||||||||||||||||
вычисляем Якобиан: |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
∂x |
|
∂x |
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
∂ρ |
|
∂θ |
∂z |
|
cos θ |
−ρsin θ |
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|||||||||
|
i |
|
= |
∂y |
|
∂y |
∂y |
= |
sin θ |
ρcos θ |
0 |
|
|
= ρcos2 θ +ρsin 2 θ = ρ |
||
|
|
|||||||||||||||
|
|
∂ρ |
|
∂θ |
∂z |
|||||||||||
|
|
|
|
|
|
0 |
0 |
1 |
|
|
|
|||||
|
|
|
|
∂z |
|
∂z |
|
∂z |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
∂ρ |
|
∂θ |
∂z |
|
|
|
|
|
|
|
|
|
116
|
Ларин Александр Александрович “Курс высшей математики. Часть 2.” |
Итого: ∫∫∫F(x, y, z)dxdydz = ∫∫∫F(ρcos θ,ρsin θ, z)ρdθdρdz |
|
r |
τ |
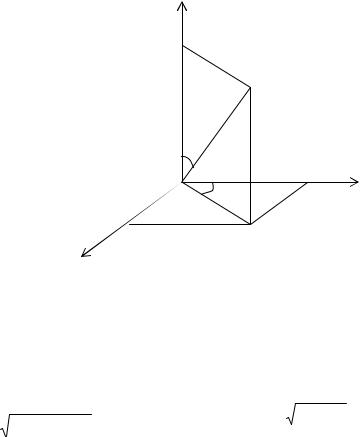
Сферическая система координат.
z
P
ρ
ϕ
0 |
θ |
x |
y
Связь координат произвольной точки Р пространства в сферической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:
x = ρsin ϕcos θy = ρsin ϕsin θ
z = ρcos ϕ
|
|
|
|
|
|
|
|
ρ = |
x2 + y2 + z 2 ; θ = arctg |
y |
; |
ϕ = arctg |
x2 + y2 |
; |
||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
z |
||
|
|
|
|
Для представления тройного интеграла в сферических координатах вычисляем |
||||||||||||||
Якобиан: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
∂x |
|
∂x |
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
∂ρ |
∂ϕ |
|
∂θ |
|
sin ϕcos θ |
ρcos ϕcos θ |
−ρsin ϕsin θ |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||||
|
i |
|
= |
∂y |
|
∂y |
|
∂y |
= |
sin ϕsin θ |
ρcos ϕsin θ |
ρsin ϕcos θ |
|
= cos ϕ(ρ2 sin ϕcos ϕcos2 θ+ |
||||
|
|
|||||||||||||||||
|
|
∂ρ |
∂ϕ |
|
∂θ |
|||||||||||||
|
|
|
|
|
|
cos ϕ |
−ρsin ϕ |
|
|
0 |
|
|
|
|
||||
|
|
|
|
∂z |
|
∂z |
|
∂z |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
∂ρ |
∂ϕ |
|
∂θ |
|
|
|
|
|
|
|
|
|
|
|
+ ρ2 sin ϕcos ϕsin 2 θ) +ρsin ϕ(ρsin 2 ϕcos2 θ+ρsin 2 ϕsin 2 θ) = ρ2 cos2 ϕsin ϕ+ρ2 sin3 ϕ =
= ρ2 sin ϕ.
Окончательно получаем:
∫∫∫F(x, y, z)dxdydz = ∫∫∫f (ρ,ϕ,θ)ρ2 sin ϕdρdϕdθ
r τ
117
Ларин Александр Александрович “Курс высшей математики. Часть 2.”
Геометрические и физические приложения кратных интегралов. 1) Вычисление площадей в декартовых координатах.
y
|
|
|
y = ϕ(x) |
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
a |
|
y = f(x) |
b |
|
x |
|
|
|
|
|||
|
|
|
|
|||
Площадь S, показанная на рисунке может быть вычислена с помощью двойного |
||||||
интеграла по формуле: |
ϕ( x) |
|
|
|
||
b |
|
|
|
|||
S = ∫ |
∫dydx |
|
|
|
||
a f ( x)
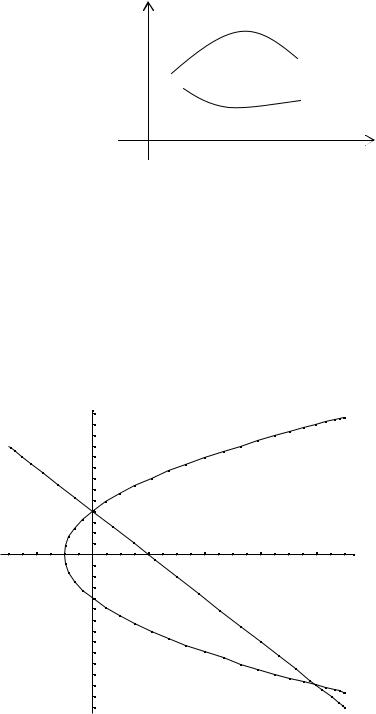
Пример. Вычислить площадь фигуры, ограниченной линиями y2 = 4x + 4; x + y – 2 = 0.
Построим графики заданных функций:
|
6 |
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
-2 |
2 |
4 |
6 |
8 |
|
-2 |
|
|
|
|
-4 |
|
|
|
|
-6 |
|
|
|
|
Линии пересекаются в двух точках – (0, 2) и (8, -6). Таким образом, область |
||||||||||||||||||
интегрирования ограничена по оси Ох графиками кривых от |
x = |
y2 |
− 4 |
до х = 2 – у, а |
|||||||||||||||
|
|
4 |
|||||||||||||||||
по оси Оу – от –6 до 2. Тогда искомая площадь равна: |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
2 |
2−y |
2 |
y |
2 |
− 4 |
|
2 |
− 4y − y |
2 |
+ 4 |
|
|
1 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||
S = ∫ ∫ |
|
|
|
|
8 |
|
|
= |
∫(− y |
− 4y +12)dy = |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
dxdy = ∫ 2 − y − |
|
|
4 |
dy = ∫ |
4 |
|
|
dy |
4 |
|
|||||||||
−6 y2 −4 |
−6 |
|
|
|
−6 |
|
|
|
|
−6 |
|
|
|
|
|||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
118

|
|
|
|
|
|
|
|
|
Ларин Александр Александрович “Курс высшей математики. Часть 2.” |
||||||||||||||||||
|
1 |
|
|
y3 |
|
4y2 |
|
2 |
|
1 |
|
|
8 |
36 6 |
|
4 |
36 |
|
1 |
|
|
8 |
|
1 |
|
||
= |
|
|
− |
|
− |
|
+12y |
|
= |
|
|
− |
|
−8 + 24 − |
|
− |
|
|
−12 6 = |
|
88 |
− |
|
|
= 21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
4 |
|
|
3 |
|
2 |
|
|
|
4 |
|
|
3 |
|
3 |
|
|
2 |
|
4 |
|
|
3 |
|
3 |
|
|
|
|
|
|
−6 |
|
|
|
|
|
|
|
|
|
||||||||||||||
2) Вычисление площадей в полярных координатах.
θ2 ϕ(θ)
S = ∫∫ρdρdθ = ∫∫dydx = ∫ ∫ρdρdθ
τθ1 f (θ)
3)Вычисление объемов тел.
Пусть тело ограничено снизу плосткостью ху, а сверху– поверхностью z = f(x,y), а с боков – цилиндрической поверхностью.
Такое тело называется цилиндроид.
z
z = f(x, y)
x1 |
y1 |
x2 |
x
y2
y
V = limx→0 ∑∑ |
x2 |
y2 |
z y x = ∫∫zdydx = ∫∫zdydx |
||
|
x1 |
y1 |
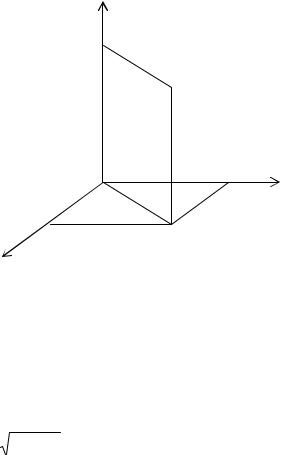
Пример. Вычислить объем, ограниченный поверхностями: x2 + y2 = 1; x + y + z =3 и плоскостью ХОY.
119

Ларин Александр Александрович “Курс высшей математики. Часть 2.”
Пределы интегрирования: по оси ОХ: y = − 1− x2 |
; |
y |
2 |
= 1− x2 |
; |
|
|
1 |
|
|
|
|
|
по оси ОY: x1 = -1; x2 = 1; |
|
|
|
|
||
1 |
1−x |
|
|
|
|
|
V = ∫ |
∫(3 − x − y)dydx = 3π; |
|
|
|
|
|
−1− 1−x2
1−x2
4) Вычисление площади кривой поверхности.
Если поверхность задана уравнением: f(x, y, z) = 0, то площадь ее поверхности находится по формуле:
|
∂f 2 |
|
∂f |
2 |
∂f 2 |
|
||
|
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
||||
S = ∫∫ |
|
∂x |
|
∂y |
|
∂z |
dydx |
|
|
|
|
∂f |
|
|
|
||
∂z
Если поверхность задана в неявном виде, т.е. уравнением z = ϕ(x, y), то площадь этой поверхности вычисляется по формуле:
|
∫∫ |
|
∂z 2 |
|
∂z 2 |
|
||
|
|
|
|
|
|
|
|
|
S = |
|
1 |
+ |
|
+ |
|
|
dydx |
|
|
|
|
∂x |
|
∂y |
|
|
5)Вычисление моментов инерции площадей плоских фигур.
Пусть площадь плоской фигуры (область ) ограничена линией, уравнение которой f(x,y) = 0. Тогда моменты инерции этой фигуры находятся по формулам:
-относительно оси Ох: I x = ∫∫y 2 dydx
-относительно оси Оу: I y = ∫∫x2 dydx
-относительно начала координат: I0 = I x + I y = ∫∫(x2 + y 2 )dydx - этот момент инерции называют еще полярным моментом инерции.
6) Вычисление центров тяжести площадей плоских фигур.
Координаты центра тяжести находятся по формулам:
xC = |
∫∫wxdydx |
yC = |
∫∫wydydx |
||
|
; |
|
; |
||
∫∫wdydx |
∫∫wdydx |
||||
здесь w – поверхностная плотность (dm = wdydx –масса элемента площади).
120
