Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Высшая матматика том2

.pdf

Скачиваний:

Добавлен:

11.04.2015

Размер:

1.31 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 134 5 6 7 8 9 10 11 12 13 > Следующая >>>

Ларин Александр Александрович “Курс высшей математики. Часть 2.” f ′′(c1 ) < 0 , следовательно, y − y < 0 .

Пусть x < x0 тогда x < c < c1 < x0 и x – x0 < 0, c – x0 < 0, т.к. по условию f ′′(c1 ) < 0, то y − y < 0 .

Аналогично доказывается, что если f′′(x) > 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).

Теорема доказана.

Определение. Точка, отделяющая выпуклую часть кривой от вогнутой,

называется точкой перегиба.

Очевидно, что в точке перегиба касательная пересекает кривую.

Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f′′(a) = 0 или f′′(a) не существует и при переходе через точку х = а f′′(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.

Доказательство. 1) Пусть f′′(x) < 0 при х < a и f′′(x) > 0 при x > a. Тогда при x < a кривая выпукла, а при x > a кривая вогнута, т.е. точка х = а – точка перегиба.

2)Пусть f′′(x) > 0 при x < b и f′′(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Тогда x = b – точка перегиба.

Теорема доказана.

Асимптоты.

При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.

Определение. Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.

Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой.

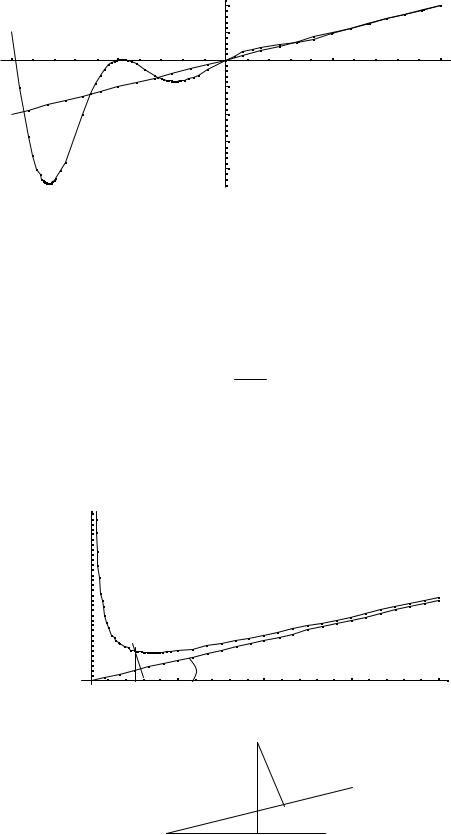
Вообще говоря, кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном ниже графике

−x

функции y = x + e 3 sin x . Ее наклонная асимптота у = х.

	Ларин Александр Александрович “Курс высшей математики. Часть 2.”
		10
		5
-10	-5	5	10
		-5
		-10
		-15
		-20
Рассмотрим подробнее методы нахождения асимптот кривых.

	Вертикальные асимптоты.
Из определения асимптоты следует, что если lim						f (x) = ∞ или	lim f (x) = ∞
				x	→a+0		x→a−0
или lim f (x) = ∞ , то прямая х = а – асимптота кривой y = f(x).
x→a
Например, для	функции	f (x) =	2	прямая	х	= 5 является	вертикальной
асимптотой.			x −5
асимптотой.
	Наклонные асимптоты.
Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b.
15
12.5
10
7.5
5
2.5
		1	2		3	4

ϕ P

Обозначим точку пересечения кривой и перпендикуляра к асимптоте – М, Р – точка пересечения этого перпендикуляра с асимптотой. Угол между асимптотой и осью Ох обозначим ϕ. Перпендикуляр МQ к оси Ох пересекает асимптоту в точке N.

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

Тогда MQ = y – ордината точки кривой, NQ = y - ордината точки N на

асимптоте.

По условию: lim

= 0 ,

NMP = ϕ,

x→∞

cosϕ

Угол ϕ - постоянный и не равный 900, тогда

lim

= lim

cosϕ = lim

= 0

x→∞

NM = MQ − QN = y − y = f (x) −(kx +b)

Тогда lim[ f (x) −(kx + b)] = 0 .

x→∞

Итак, прямая y = kx + b – асимптота кривой. Для точного определения этой прямой необходимо найти способ вычисления коэффициентов k и b.

В полученном выражении выносим за скобки х:

	f (x)			b
lim x			− k −		= 0
		x
x→∞				x

Т.к. х→∞, то

f (x)

− k

−

= 0 , т.к. b = const, то lim

= 0;

lim k = k .

lim

x→∞

x→∞ x

x→∞

Тогда lim

f (x)

− k − 0 = 0 ,

следовательно,

x→∞

k = lim

f (x)

x→∞

Т.к. lim[f (x) −(kx +b)]= 0 , то

lim[f (x) − kx]− lim b = 0 , следовательно,

x→∞

b = lim[f (x) − kx]

x→∞

Отметим, что горизонтальные асимптоты являются частным случаем наклонных асимптот при k =0.

Пример. Найти асимптоты и построить график функции y = x2 + 2x −1 . x

1) Вертикальные асимптоты: y→+∞ x→0-0:				y→-∞				x→0+0, следовательно, х = 0-
вертикальная асимптота.
2) Наклонные асимптоты:
k = lim	x2	+ 2x −1			2		1
			= lim 1+			−			=1
		x2	= lim 1+		x	−	x2		=1
x→∞		x2	x→∞		x		x2

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

+ 2x −1

+ 2x −1− x

2x −1

= lim

= lim 2

−

= 2

b = lim( f (x) − x) = lim

− x

= lim

x→∞

Таким образом, прямая у = х + 2 является наклонной асимптотой.

Построим график функции:			6
			6
			4
			2
-3	-2	-1	1	2	3
			-2

Пример. Найти асимптоты и построить график функции

y =

− x2

Прямые х = 3 и х = -3 являются вертикальными асимптотами кривой.

Найдем наклонные асимптоты: k = lim

= 0

− x2

x→∞ 9

b = lim

= lim

= 0

9 − x2

x→∞

−1

y = 0 – горизонтальная асимптота.

			6
			4
			2
-7.5	-5	-2.5	2.5	5	7.5
			-2
			-4
			-6

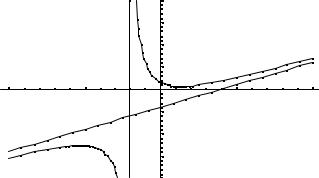
Пример. Найти асимптоты и построить график функции y =	x2	− 2x +3		.
		x +	2

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

Прямая х = -2 является вертикальной асимптотой кривой.

Найдем наклонные асимптоты.


					2		3
	x2 − 2x + 3		x2 − 2x + 3		1−		+
k = lim	x2 − 2x + 3	= lim	x2 − 2x + 3	= lim	1−	x	+		x2	=1.
k = lim	x(x + 2)	= lim	x2 + 2x	= lim			2			=1.
x→∞	x(x + 2)	x→∞	x2 + 2x	x→∞			2
					1+
					1+			x

− 2x

− 2x + 3 − x

− 2x

− 4x +3

− 4 +

= lim

= −4

b = lim

x + 2

− x

= lim

x + 2

x→∞

Итого, прямая у = х – 4 является наклонной асимптотой.

		20
		15
		10
		5
-10	-5	5	10
		-5
		-10
		-15
		-20

Схема исследования функций

Процесс исследования функции состоит из нескольких этапов. Для наиболее полного представления о поведении функции и характере ее графика необходимо отыскать:

1) Область существования функции.

Это понятие включает в себя и область значений и область определения функции.

2)Точки разрыва. (Если они имеются).

3)Интервалы возрастания и убывания.

4)Точки максимума и минимума.

5)Максимальное и минимальное значение функции на ее области определения.

6)Области выпуклости и вогнутости.

7)Точки перегиба.(Если они имеются).

8)Асимптоты.(Если они имеются).

9)Построение графика.

Применение этой схемы рассмотрим на примере.


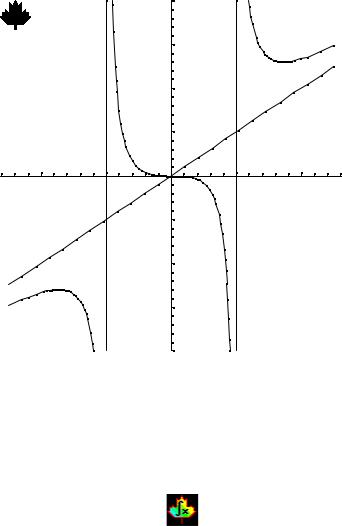
Пример. Исследовать функцию	y =	x3		и построить ее график.
		x2	−1

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

Находим область существования функции. Очевидно, что областью определения функции является область (-∞; -1) (-1; 1) (1; ∞).

В свою очередь, видно, что прямые х = 1, х = -1 являются вертикальными асимптотами кривой.

Областью значений данной функции является интервал (-∞; ∞). Точками разрыва функции являются точки х = 1, х = -1.

Находим критические точки.

Найдем производную функции

′

3x2

(x2 −1) − 2x x3

3x4 −3x2 − 2x4

x4 −3x2

(x2 −1)2

= (x2 −1)2

Критические точки: x = 0; x = - 3 ; x =

3 ;

x = -1; x = 1.

Найдем вторую производную функции

y′′ =

(4x3 −6x)(x2 −

1)2

−(x4 −3x2 )4x(x

2 −1)

−1)4

(4x3

− 6x)(x4 − 2x2

+1) − (x4 −3x2 )(4x3 − 4x)

(x2

−1)4

4x7

−8x5 + 4x3 − 6x5 +12x3 − 6x − 4x7 + 4x5 +12x5 −12x3

(x2

−1)4

2x5 +

4x3 −6x

2x(x4 + 2x2

−3)

2x(x2 +

3)(x2

−1)

2x(x2

+3)

(x2

−1)4

(x2 −1)4

(x2

−1)4

−1)3

Определим выпуклость и вогнутость кривой на промежутках.

-∞ < x < -		3 ,	y′′ < 0,	кривая выпуклая
-	3 < x < -1,		y′′ < 0,	кривая выпуклая
-1 < x < 0,			y′′ > 0, кривая вогнутая
0	< x < 1,		y′′ < 0, кривая выпуклая
1	< x <	3 ,	y′′ > 0, кривая вогнутая
	3 < x < ∞,		y′′ > 0, кривая вогнутая

Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.

-∞ < x < -		3 ,	y′ > 0, функция возрастает
-	3 < x < -1,		y′ < 0, функция убывает
-1 < x < 0,			y′ < 0, функция убывает
0	< x < 1,		y′ < 0, функция убывает
1	< x <	3 ,	y′ < 0, функция убывает
	3 < x < ∞,		y′′ > 0, функция возрастает

Видно, что точка х = - 3 является точкой максимума, а точка х = 3 является точкой минимума. Значения функции в этих точках равны соответственно -3 3 /2 и 3 3 /2.

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

Про вертикальные асимптоты было уже сказано выше. Теперь найдем

наклонные асимптоты.

k = lim

= lim

=1;

2 −1

x→∞ x

x→∞

1−

− x

+ x

= lim

= 0

b = lim

−1

− x

= lim

−1

x→∞ x

x→∞

x→∞ x

x→∞

−

Итого, уравнение наклонной асимптоты –

y = x.

Построим график функции:

		4
		3
		2
		1
-2	-1	1	2
		-1
		-2
		-3
		-4

При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая проводит полное исследование функций по приведенной выше схеме. Достаточно ввести функцию, программа выведет подробный отчет о результатах исследования по каждому пункту.

Для запуска программы дважды щелкните по значку:

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (© Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

Векторная функция скалярного аргумента.

A(x, y, z)

r(t) − r0

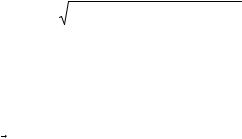
Пусть некоторая кривая в пространстве задана параметрически: x = ϕ(t); y = ψ(t); z = f(t);

Радиусвектор произвольной точки кривой: r = xi + yj + zk = ϕ(t)i +ψ(t) Gj + f (t)kG .

Таким образом, радиусвектор точки кривой может рассматриваться как некоторая векторная функция скалярного аргумента t. При изменении параметра t изменяется величина и направление вектора r .

Запишем соотношения для некоторой точки t0:

limϕ(t) = ϕ0 ; limψ(t) =ψ0 ;

lim f

rG = ϕ

t→t0

Тогда вектор

i +ψ

Gj + f

kG - предел функции r (t).

Очевидно, что

lim

rG(t) − rG

= lim

(ϕ(t) −ϕ

+ (ψ(t) −ψ

)2 + (f (t) − f

t→t0

rG(t)

lim

t→t0

(t) = f0 ;

limt t r (t) = rG0 .

→ 0

= 0 , тогда

Чтобы найти производную векторной функции скалярного аргумента, рассмотрим приращение радиусвектора при некотором приращении параметра t.

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

r (t)

r (t +

rG(t + t) =ϕ(t + t)i +ψ(t + t) j + f (t + t)k ;

r = r (t + t) − r (t) ;

rG = (ϕ(t + t) −ϕ(t))i + (ψ(t + t) −ψ(t)) j + ( f (t + t) − f (t))k

ϕ(t + t) −ϕ(t) G

ψ(t + t) −ψ(t)

f (t + t) − f (t) G

или, если существуют производные ϕ′(t), ψ′(t), f′(t), то

′

lim

+ f

= r

′

=ϕ (t)i

+ψ

(t) j

(t)k

t→0

Это выражение – вектор производная вектора r .

j +

′

= [ϕ (t)]

+[ψ (t)]

+[f (t)]

Если имеется уравнение кривой:

x = ϕ(t);

y = ψ(t);

z = f(t);

то в произвольной точке кривой А(xА, yА, zА) с радиусвектором

r = xiG + yj + zk = ϕ(t)i + ψ(t) j + f (t)k

можно провести прямую с уравнением

x − xA

y − yA

z − zA

Т.к. производная

- вектор, направленный по касательной к кривой, то

x − xA

y − yA

z − zA

dxA

dyA

dzA

Свойства производной векторной функции скалярного аргумента.

(rG

+ rG

− rG ) =

drG1

drG2

−

dr3

d(λr )

= λ

, где λ = λ(t) – скалярная функция

d(rG1 rG2 )

dr1

+ rG

drG2

Ларин Александр Александрович “Курс высшей математики. Часть 2.”

4)	d(rG1 ×rG2 )	=	drG1	×rG	+ rG	×	dr2

	dt		dt	2	1		dt

Уравнение нормальной плоскости к кривой будет иметь вид:


	dxA	(x − xA ) +	dyA	( y − yA ) +		dz A	(z − z A ) = 0
	dt
			dt			dt
Пример. Составить уравнения касательной и нормальной плоскости к линии,
заданной уравнением rG = i cost + j sin t +					3tk в точке t = π/2.

Уравнения, описывающие кривую, по осям координат имеют вид:

x(t) = cost; y(t) = sint; z(t) = 3t ;

Находим значения функций и их производных в заданной точке:

x′(t) = -sint; x′(π/2) = -1; x(π/2) = 0;

-это уравнение касательной.

		y′(t) = cost;						′	3
		y′(t) = cost;						z (t) =	3
		y′(π/2) = 0;						z′(π/2)= 3
		y(π/2) = 1;						z(π/2)= π	3 /2
x		y −1		z −	π		3
x	=	y −1	=	z −		2

−1		0		3

Нормальная плоскость имеет уравнение:

−1 (x − 0) + 0 + 3(z −	π 3	) = 0
	2

− x + 3z − 32π = 0

Параметрическое задание функции.

Исследование и построение графика кривой, которая задана системой уравнений

вида:

x = ϕ(t)

y = ψ(t) ,

производится в общем то аналогично исследованию функции вида y = f(x).

Находим производные:

dxdt = ϕ′(t)

dy = ψ′(t)dt

<<< < Предыдущая 1 2 34 / 134 5 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.04.2015136.6 Кб12бу.docx
#
11.04.2015254.98 Кб137ВВЕДЕНИЕ В КОМПЬЮТЕРНУЮ ГРАФИКУ Лекция 1.doc
#
11.04.2015158.93 Кб30ведущий курсяк.docx
#
11.04.201580.1 Кб5вот как бывает.docx
#
11.04.2015529.91 Кб11вто моеWord.docx
#
11.04.20151.31 Mб14Высшая матматика том2.pdf
#
11.04.2015334.96 Кб21геоморф.docx
#
11.04.2015580.61 Кб96ГОТОВЫЙ КУРСЯК.doc
#
11.04.201548.6 Кб12давно на палочке.docx
#
11.04.2015978.85 Кб222Декоративная дендрология -ЛА(ФЗО).pdf
#
11.04.201532.62 Кб33дендрология.docx