Дифференциальные уравнения равновесия жидкости

Выделим находящейся внутри покоящейся жидкости, элементарный объем в виде параллелепипеда с ребрами dx, dy, dz, параллельными осям координат.

Отбросим мысленно окружающую параллелепипед жидкость, заменив ее действие на грани соответствующими силами гидростатического давления.

Масса рассматриваемого элемента жидкости

dm = ρ·dV = ρ·dx·dy·dz.

Для равновесия выделенного элемента жидкости необходимо, чтобы сумма проекций всех действующих сил на любую из координатных осей была равна нулю.

Обозначим через a_x, a_y, a_z проекции всех ускорений массовых сил, отнесенных к единице массы, на оси x, y, z. Тогда проекции всех массовых сил на координатные оси

Гидростатическое давление является функцией координат точки и изменяется в направлении каждой из осей координат. Приращение давления по оси х составит , тогда давление в конце грани будет.

Проекция разности сил гидростатического давления на левую и правую грани выделенного элемента равна

.

Аналогичным образом можно найти элементарные силы, действующие на остальные четыре грани.

Так как кроме рассмотренных других сил нет, то для равновесия массы выделенного элемента силы давления должны уравновешивать массовые силы. Получаем систему уравнений равновесия для рассматриваемого объема жидкости

После приведения подобных и сокращения оставшихся слагаемых на dxdydz получим уравнения равновесия жидкости в дифференциальной форме, выведенные в 1755 г. Л. Эйлером:

где р – искомое давление как функция координат.

Для приведения уравнений Эйлера к виду, удобному для интегрирования, умножим каждое из уравнений соответственно на dx, dy, dz и сложим почленно:

где dp – полный дифференциал давления p.

Полученное уравнение выражает функциональную зависимость давления от рода жидкости и координат точки в пространстве и позволяет определить значение давления в любой точке жидкости, находящейся в равновесии. Это уравнение справедливо для капельных жидкостей и для газов, причем для газов дополнительным условием равновесия является уравнение Менделеева-Клайперона.

Можно легко получить уравнение поверхности равного давления - поверхности, давление во всех точках которой одинаково (р = const).

При р = const dp = 0, а так как плотность не может быть равно нулю, следовательно,

Это уравнение поверхности равного давления, частным случаем которой является свободная поверхность жидкости.

Рассмотрим несколько конкретных примеров и установим, какой вид будет иметь поверхность равного давления (в том числе и свободная поверхность) в этих случаях.

Пример 1. Жидкость находится в равновесии в резервуаре в поле действия только силы тяжести.

В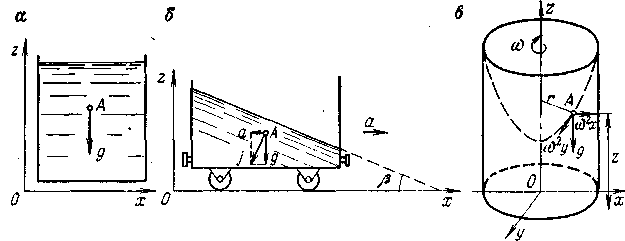этом случае проекции результирующей единичных массовых сил будут:a_Х= 0, a_Y = 0, a_Z= -g. Получим -gdz=0 или после интегрирования

Это - уравнение горизонтальной плоскости. Следовательно, в покоящейся однородной жидкости (р=idem) любая горизонтальная плоскость является плоскостью равного давления.

Пример 2. Жидкость находится в равновесии в резервуаре, движущемся горизонтально с некоторым ускорением а.

Вэтом случае любая частица жидкости находится под действием ускоренийа и g, следовательно, проекции результирующей единичных массовых сил будут:

a_X = -a, a_Y =0, a_Z = -g.

Подставляя эти значения в уравнение поверхности равного давления, получим -adx - gdx = 0 или после интегрирования

ах + gz= const.

Это - уравнение наклонной плоскости. Следовательно, в данном случае поверхности равного давления представляют собой плоскости, наклонные к осям Ох и Оz и параллельные оси Оу. Угол наклона плоскости к горизонту может быть найден из выражения β= arctg (a/g).

Пример 3. Жидкость находится в равновесии в цилиндрическом резервуаре, вращающемся вокруг вертикальной оси с постоянной угловой скоростью ω.

В этом случае любая частица жидкости находится под действием ускорений силы тяжести g и центробежной силы инерции ω ²г, следовательно, проекции результирующей единичных массовых сил будут: a_X = ω²x, a_Y = ω²y, a_Z = -g. Подставляя эти значения в уравнение, получим ω²xdx + ω²ydy –gdz=0 или после интегрирования

но так как то

Это - уравнение параболоида вращения. Следовательно, в данном случае поверхности равного давления представляют собой семейство параболоидов вращения вокруг вертикальной оси. При сечении их вертикальной плоскостью получится семейство парабол с вершинами на оси Оz, а при сечении горизонтальной плоскостью - семейство концентрических окружностей с центром на оси Оz.

В последних двух примерах рассмотрены случаи так называемого относительного покоя жидкости, когда она находится в резервуарах, движущихся тем или иным образом с постоянным ускорением, но частицы жидкости не перемещаются друг относительно друга и относительно стенок резервуара.