Лекция №4 Полиномиальное распределение (схемы)

Цветов шаров в урне больше 2-х, 1,2,……….N –цвета.

Из урны, содержащей такие шары, формируется выборка длиной n. Длина выборки n –это число выборок m:

m1- шаров с номером 1-ого цвета,

m2-шаров с номером 2-ого цвета,

- шаров с N-цветом.

Фиксируем номер шара и число выборки и используем принцип пересчета.

- вероятность появления объекта с номером N в одном элементарном опыте.

Распределение полинома - проводится серия независимых опытов, испытаний. В отдельном опыте может произойти один из N исхода.

Ассимтотические приближения биноминального распределения (для схемы Бернулли)

Проводятся испытания длиной N. Многие решения, которые базируются на этой схеме, используют вероятность такого события. Требуется определить вероятность того, что из n независимых испытаний успех произойдет m раз.

(*) - формула биноминального распределения

Если серия испытаний продолжительна. Преобразовать при большихN, чтобы улучшить ее наглядность.

3Способа аппроксимации данной формулы:

1. замена формулы (*) законом Пуассона. Если считать, что n, ,mp==const

Если на графике отложить целочисленные значения m, будет огибающая.

2. Локальная теорема Муавра-Лапласса, она предлагает вариант заме6ны (*) с помощью:

q=1-p,

n – число испытаний

- локальная теорема Муавра-Лапласса

р - малая, но конечная величина

3. Интегральная теорема Муавра-Лапласа

Р{a

Важное место занимает оценка точности этих исследований. Формируется выборка множества объектов респондентов, называемая выборкой. Попадание респондента в выборку есть случайное событие.

P(A)

Требуется определить V выборки, n-частота событий, рассчитанная по которой вероятность отличается от заданной вероятности Р не больше, чем на .

(***)

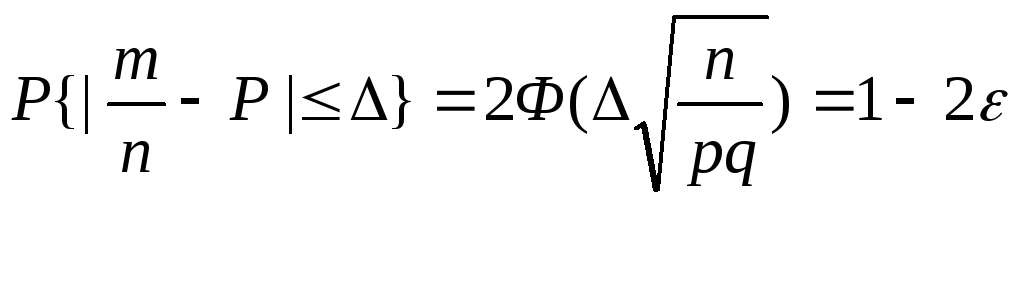- малая величина

Из уравнения (***) найдем значение аргумента функции Ф.

Лекция №5 Случайная величина

Случайная величина – это базовая вероятностная модель, которая широко используется при описании вероятностных явлений, в различных областях техники и науки, в том числе при проектировании информационных систем.

Случайной величиной называют функцию (известную функцию), которая ставит в однозначное соответствие случайному событию число:

X= φ (A); (1)

где X – случайная величина;

φ (А) – известная функция (правило);

А - случайное событие.

Если подставим случайное событие, то получим число. Смысл введения модели случайной величины заключается в том, чтобы от случайного события перейти к числовому образу этого события или перейти к числу.

Общая схема этого отображения

С событием А связан некий эксперимент, представленный множеством элементарных исходов:

А Е: Ώ = (ω_1, ω_2,…,ω_n);

Чтобы определить событие А, нужно сформировать множество Ώ, и на нем определить те элементарные исходы, которые связаны с событием А:

A_i = (ω_i1, ω_i2,…, ω_ik) (*);

C числом связана числовая ось

x

x₁ x

Берем произвольную точку x и относительно этой точки располагаем те элементарные события, которые связаны с событием А_i. Пользуясь определением случайной величины (1) рассмотрим расположение чисел x_1,которое определяется по правилу (1) как функция ω_i1, получаем точку x₁:

x_{1 =} φ (ω_i1); x₂ = φ (ω_i2); …; x_n = φ (ω_in).

Первое условие

Используя такое представление для произвольного события А для некоторого числа x, можно ввести событие:

ξ= φ (ω_i); (1а)

где ξ - точка на числовой оси;

φ (ω_i) –элементарное случайное событие.

Событие А заключается в том, что ξ будет меньше, чем точка, выбранная на числовой оси:

А : ξ < x;

Тогда это событие произойдет. После того как выберем точку, необходимо выяснить попадет ли выбранное событие А, при этом нас интересует случайное событие левее точки x. Значение x будет увеличиваться.

С точкой x связаны, таким образом, некоторые вероятностные свойства рассматриваемого события, чтобы описать зависимость вероятностных свойств этого события ( с учетом определения (1)) мы можем говорить о соответствующей случайной величине x; следует ввести функцию F_ξ(x), которая отражает закономерность случайной величины ξ от положения точки x на числовой оси. Эту функцию будем обозначать

F_ξ(x) = P {ξ ≤x}; (2)

Вероятность такого события, что значение случайной величины будет больше нами выбранного значения x. По правилу (1а) конкретное значение ξ в формуле (1а), тогда подставим ω_{i –} элементарный исход, получим конкретное значение случайной величины – реализация случайной величины.

Второе условие

Чтобы не вводить дополнительного обозначения для случайной величины, будем в общем случае обозначать ее заглавной X.

ξ = X, тогда функция F(x) по выражению (2):

F(x) = P {X ≤x}; (3)

Третье условие

Функцию F(x) называют функцией распределения случайной величины, хотя на самом деле распределяется вероятность этой случайной величины.

Виды представления случайных величин

1.Учитывая, что правило формирования случайной величины (1), правила формирования случайного события A_i, которому соответствует случайная величина X, соответствует событию A_i.

Если возьмем каждое благоприятствующее событие φ (ω_i2) подставим в (1), получим одно из значений случайной величины – реализацию случайной величины.

X = (x₁,x₂,…,x_k)

Случайная величина есть множество реализаций. Поскольку элементарные исходы независимые события, то и реализации есть независимые случайные числа.

2.Описание вероятностных свойств случайной величины. В общем случае задается выражением (2) или функцией F(x) распределения вероятностей. По определению функция F(x) – равная описывающая вероятность события, как X≤x, есть сумма тех реализаций, не превышающих x:

F(x) = P {X≤x}=∑ P(x_i)

x_i≤x

Чтобы уточнить особенность функции следует разделить все множество случайных величин на 2 группы:

1) Дискретные случайные величины; дискретной случайной величиной называют случайную величину, множество реализаций которой конечна, либо счетно (все реализации можно пронумеровать числами натурального ряда ).

2) Если число реализаций бесконечно, то такие случайные величины называют непрерывными, которые определены на отрезке [a,b], и на нем может принимать любое значение.

Рассмотрим общие свойства функции распределения случайной величины X. Если случайная величина может принимать любые значения внутри отрезка [a,b], то функция F(x) должна обладать такими свойствами:

• F(a) = 0, т.к. нет таких реализаций (a<x);

• F(b) = 1;

• P {α≤X≤β} = F(β) - F(α).

Для дискретной случайной величины ее вероятностные свойства удобно задавать в виде таблицы:

xi	x1	x2	…	xn
P(xi)	P(x1)	P(x2)	…	P(xn)

x – реализации.

Закон распределения дискретной случайной величины

P(x)

P(x₄)

P(x₂)

P(x₁) P(x5)

P(x₃)

x

x₁ x₂ x₃ x₄ x₅

Этот график еще называют полигон вероятности.

_n

∑ P(x_i) = 1

ⁱ⁼¹

Построим функцию распределения дискретной случайной величины:

F(x) = P {X ≤x};

F(x)

1

P(x₁) x

a x₁ x₂ x₃ x_n b

Если есть ≥, то в точке а может появиться случайная величина, если <, то в точке а вероятность равна 0.