Лекция № 9
Энтропия –это средняя мера неопределенности, связанная с неопределенностью одного выбора (одной реализации), осуществляем выбор одной из реализаций.
Энтропия-плотность распределения, измеряется в битах.
Системы случайных величин
Является развитие модели случайная величина. Необходимость использования обусловлена тем, что в практических задачах возникает ситуация, когда случайному событию необходимо поставить в соответствие набор чисел.
Если распространить на большое число координат, то точка набора будет характеризоваться набором координат. Числа будут изменяться от опыта к опыту. Следует изучить вероятностные свойства такой модели. Изучения начинают с конструирования обобщенного определения, им является система случайных величин.
Система- есть двойка
А-множество элементов
R- множество отношений между элементами- взаимосвязь.
Системой случайных величин называют функцию, правило от случайного события, ставящего в однозначное соответствие событию последовательность чисел.
Первичным является
некоторый эксперимент Е(1). Рассматриваем
множество элементарных исходов. На
множестве
перечисляем те элементарные исходы,
которые связаны с появлением
Формируем правило
- каждому элементарному исходу ставит
в соответствие номер чисел.
Каждая составляющая последовательность есть случайная величина.
Каждая позиция
системы – случайная величина. Фактически
мы имеем дело с одним число. Наблюдаем
реализацию
. Последовательность меняется от исхода
к исходу. Зафиксируем место в
последовательности.
I – определяем 1-ую случайную величину,
II – определяем l -ую случайную величину. Некоторому элементарному исходу соответствует последовательность чисел.
……
- это и
есть строчка в таблице.
Все числа в этой числовой последовательности есть реализации соответствующих случайных величин.
Множество А представлено числом случайных величин в системе l. Примерами отношения R является отношение зависимости между числами, координатами в этой последовательности. Чтобы выявить характер отношения между случайными величинами, входящими в систему , вводят в рассмотрение характеристику вероятностных свойств, входящих в систему. Для описания вероятностных свойств случайных величин, входящих в систему по аналогии с одной случайной величиной вводят функцию совместного распределения вероятности (функцию совместных вероятностей), системы случайных величин.
-
функция позволяет рассчитать вероятностные
свойства,
X- рассматривается как детерминированная функция.
Поскольку говорим по аналогии , то для одновременного случая функция распределения есть вероятность.
Произошло совместное событие.
Функция совместного распределения вероятности. Если функция известна, то вероятностные свойства системы вписаны. Рассмотрим какими общими свойствами обладает функция.
Вводим упрощение. Пусть даны 2 переменные:
;
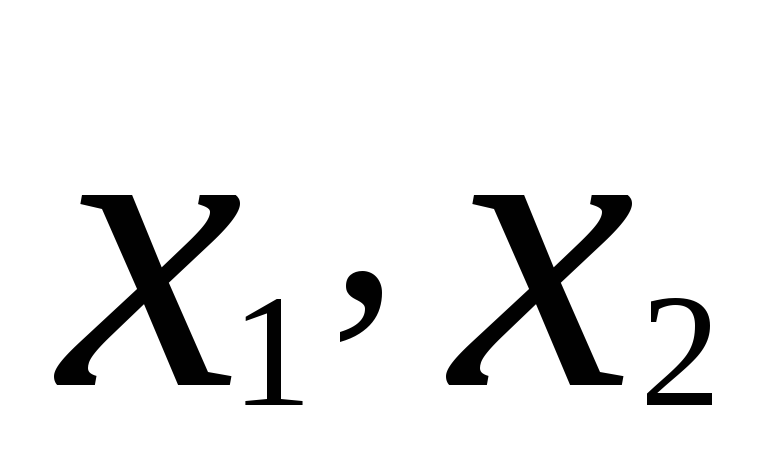а=-
F(
)
– функция задана на плоскости
(1)
Рассчитаем вероятность исходя из того, что функция F(x) задана.
Пользуясь формулой
(1) и выбирая
,
и выбирая такие значения , чтобы
прямоугольник считать малой величиной
и вспоминая определение частной
производной и выражения для плотности
совместного распределения случайной
величины и пользуясь формулой (1),
получаем:
Если плоскость известна, записываем следующее:
F(
)=
(2)
Можно найти интегральные свойства, пользуясь связью между ними.
Связь между плотностью совместного распределения и маргинальными одномерными распределениями
Нужно определить распределение одной случайной величины от другой, чтобы найти связь, нужно вспомнить, что такое
F(
)=
Пользуясь формулой (2), можно переписать:
F(
)=
=
В качестве подынтегрального выражения выступает внутренний интеграл. Формулы открывают некоторые отношения между случайными величинами, входящими в систему.
Понятия зависимых и независимых величин, входящих в систему
Рассмотрим элементарную вероятность попадания реализации в систему случайных величин в прямоугольник, ограниченный точками
Вероятность
может быть определена 2-мя способами
в
I
- ом способе пользуемся понятием плотности
совместного распределения.
вероятность
попадания в прямоугольник со сторонами:
События могут быть
зависимыми и независимыми. Вводим
условную плотность вероятности. Если
I
– случайная величина попадет в окрестность
точки
,
тоII
– я случайная величин – в
.
-
малый отрезок()
Если условия
выполняются, то и равенства выполняются
и f(
)=
- (3) - умножения плотности распределения
случайных величин
Основываясь на
формулу(3) можем уточнить понятия
зависимости и независимости случайных
величин. Если условная плотность не
зависит от условия
,
то формула (3) упрощается.
-
справедлива, если условная плотность
равна безусловной плотности. Значение
реализации случайной величины
не зависит от того, какие значения
принимала случайная величина
.
Система из таких случайных величин
называют системой , состоящей из
независимых случайных величин. Если
формула (3)- система случайных величин.
Числовые характеристики системы случайных величин
Для системы случайных величин по аналогии одной случайной величины можно ввести систему числовых характеристик. Например: моментные характеристики. Они бывают:
моментные
центральные
Чтобы найти момент нужно взять оператор математического ожидания:
