Вешкурцев- Бычков АСКиД РЭС

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Омский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

×vúù = 10,638.

.pdf

Скачиваний:

Добавлен:

10.04.2015

Размер:

796.03 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 116 7 8 9 10 11 > Следующая >>>

к различию критериев при принятии решений. В прикладных задачах распознавания наиболее часто используются критерии Байеса, последовательного анализа или Вальда, минимального риска, минимакса, Неймана-Пирсона, наибольшего правдоподобия. Рассмотрим некоторые из них [4, 17, 2527].

Метод Байеса

Метод основан на простой формуле Байеса. Если существует состояние (дефект) dj и признак hi, встречающийся в этом состоянии, то вероятность совместного появления события P(dj , hi ) определяется выражением [4 ]

	P(dj , h i ) = P(dj )·P( hi /dj ) = P( hi ) ·		P(dj / hi ).			(2.20)
Из выражения (2.20) получаем формулу Байеса
	P(dj / hi ) =	P (dj ) P(hi /dj)		,		(2.21)
						(2.21)


		P(hi )
или	P(dj / hi ) =	P (dj ) P(hi /dj)			,	(2.22)

		N
		N

Σ P(dj) P(hi / dj )

j=1

где hi - допустимый признак, hi H , i=1 … k; dj – возможные состояния dj Def;

P (dj) - априорная вероятность проявления дефекта (состояния) dj; P(hi / dj) – априорная вероятность проявления признака у объектов с состоянием dj ; P(hi) – вероятность проявления признака hi во всех объектах независимо от состояния (дефекта) dj ; P(dj/hi ) - апостериорная вероятность появления дефекта dj при условии проявления признака hi у объекта контроля после его обследования.

В правой части (2.22) компоненты задаются априорными диагностическими

матрицами вида

	h 1 ,		h 2	, … ,
d1	u11	,	u12	, … ,
d1	u11	,	u12	, … ,
d2	u21	,	u22	, … ,
M(dj, hi ) =			. . .
dj	uj1 ,		uj2	, … ,

h i u1i

u2i

, (2.33)

uji

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

где uji – априорное значение вероятности появления признака hi при условии наличия дефекта dj , при этом по строкам должно выполняться условие

å uj i = P(hi / di ) £ 1.

Матрицей-строкой вероятностей априорных состояний (дефектов) служит зависимость:

dj	1	2	3	…	j	,	(2.24)
P(d j )	в1	в2	в3	…	вj	,	(2.24)

где вj - априорное значение вероятности проявления дефекта dj . В матрице-строке (2.24) должно выполняться условие

å P(dj ) = 1.

В реальных условиях проверок (контроля) признаки h i , характеризующие текущее состояние объекта, могут проявляться одновременно. В этом случае если предположить, что они независимы, формула Байеса примет вид

P(d j / h1,h2 ,...,hi ) =	P(di ) ∏ P(hi / d j )
		i	.	(2.25)
	m		.	(2.25)
	åP(di ) ÕP(hi / d j )
	j=1	i

Решение о типе дефекта (состояния) принимается по правилу
do = arg max P(dj /h1 ,h2, …,hi ) .	(2.26)
j
Формула Байеса может быть использована и в том случае,	когда часть

признаков имеет дискретное распределение, а другая часть – непрерывное. Для непрерывного распределения используются плотности вероятностей.

Среди методов технической диагностики метод, основанный на обобщенной формуле Байеса (2.25), находит самое широкое распространение благодаря своей простоте и эффективности. Приведенный метод имеет и недостатки: требуется

большой объем информации, недостаточно четкое	улавливание	редко
встречающихся дефектов (состояний) и др. [4]. Тем	не менее, когда объем

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

статистической информации достаточен, применение метода Байеса целесообразно как одного из наиболее надежных и эффективных методов.

Достоверность правильного диагностирования при использовании метода Байеса можно оценить по выражению [27 ]

D пд =1 − Р(e)min ,			(2.27)
где P(e)min – минимальная вероятность	ошибки при распознавании		дефектов
djÎDef :			(2.28)
Р(e)min = å P ( bi) [ 1 – max P ( d j / b i)] .			(2.28)
i	j
Здесь bi – комбинация признаков hi;	P(dj / bi) – апостериорная	вероятность
определяется по (2.22) или (2.25).
Вероятность P(bi) определяется из матриц (2.23) и (2.24)		с	учетом ее
компонентов. Предположив, что проявление признаков hi		независимое,
вероятность P( b i) вычисляется по выражению
P ( bi) = P(h1 ,h2, …, hi) = Σ P(dj) ×Õ P(hi / dj).			(2.29)
j=1	i

Метод последовательного анализа (Вальда)

Метод последовательного анализа, предложенный Вальдом, применяется для дифференциальной диагностики (распознавание двух состояний). В отличие от метода Байеса, в методе Вальда число обследований заранее не устанавливается. Их приводится столько, сколько необходимо для принятия решения с определенной степенью риска. В методе последовательного анализа рассматривается отношение вероятностей признаков (отношение правдоподобия), общая процедура которого выглядит следующим образом:

B <	p(h1 / D2)		L	p(hr / D2)	< A ,	(2.30)
	p(h1	/ D1)		p(hr / D1)

где r – номер испытания, r = 1, v-1; v- общее количество испытаний;

В, A – нижняя и верхняя граница испытаний соответственно; D1,D2 – области состояний системы.

Правило принятия решения заключается в следующем:

1)если отношение (2.30) после v-го испытания (обследования) оказывается больше A, то принимается решение о состоянии D2;

2)если отношение (2.30) после v-го обследования оказывается меньше В, то

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

принимается решение о состоянии D1.

Пусть априорно известно, что условная плотность вероятностей значений признака h контролируемого объекта подчиняется нормальному закону

распределения. Среднее значение контролируемого параметра h1 характерно для

области состояний D1, а

h2 - для области состояний D2. При этом дисперсии

параметров соответственно равны σ12

= σ 22

= σ 2 .

Составим отношение

−

2)2

f(h(1)

e−

(1)

[(h(1)−

/ D2)

2σ2

h1)2−(h(1)−h2)2]

2σ

= e

f (h

/ D1)

(h(1)−

1)2

(2.31)

(1)

e−

2σ2

где (1) – означает первое обследование (испытание). Здесь отметим, что

f (h(1) / D2 ) º

p(h(1)

/ D2 )

и f (h(1)

/ D1 ) º

p(h(1) / D1 ) .

После проведения v-го обследования возьмем логарифм от (2.31) ,

f (h / D2 )

é v

f (hV / D2 )

h2 - h1

+ h1

(1)

×××ln

êåh(i) -

×vú .

f (h(2) / D1 )

f (hV / D1 )

ëi=1

получим

(2.32)

Тогда решение об исправном или неисправном состоянии технической системы будем принимать из условия

2 +

ln B <

h2 - h1

(2.33)

åh(i)

×vú < ln A .

ëi=1

Границы A и B определяются через вероятности ошибок первого рода α и

второго рода β :

(1- β )

A £

B ³

1-α

В практических расчетах α = β= 0,05

или α = β= 0,1. Сделав преобразование над

(2.33), получим

e1 + d v < åh (i) − < e2

+d v ,

(2.34)

i=1

σ 2

1− β

d =

где e1 =

;

h2 + h1

h2 − h1

− α

h2 − h1

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

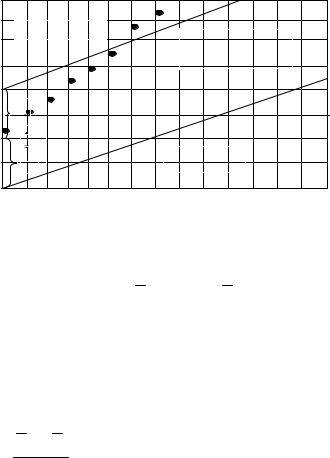
Условие (2.34)

при различном числе испытаний

v соответствует области

между двумя параллельными линиями ( рис.2.19). Если å h(i)

находится внутри

линий, то испытания продолжаются, если она выходит из

"коридора",

то

принимается решение о состоянии.

åhi

400

Неисправное

Продолжение

300

испытаний

200

100

-100

e 1

Исправное

-200

Рис. 2.19

Рассмотрим числовой пример.

Пусть σ = σ12

= σ 22

= 0.5, h1

= 2.5,

= 3,ν

= 10,

причем

h = (3,75 ; 3,72; 3,5;

3,44; 3,85; 3,66; 2,77; 2,88; 2,54)

и α = β =0,05.

Тогда А= (1-β) / α = 19;

В = β / (1-α) =

0,053;

A= 2,944; ln B = -2,944.

Отношение правдоподобия через v шагов будет равно :

h2σ-2h1 éåv h(i)

ëi=1

Следовательно, техническая система находится в неисправном состоянии, а количество шагов испытаний v < 10.

Итак, последовательные методы распознавания дефектов реализуются в виде многошаговой процедуры, на каждом шаге которой выполняется очередная проверка, а на основе полученной информации принимается решение о переходе к новой проверке объекта или остановке процесса контроля, если накопленная информация является достаточной для принятия решения о состоянии объекта.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

Метод минимального риска

Когда состояние технической системы характеризуется одним параметром (признаком), то рассматривается одномерное распределение случайного значения контролируемого параметра. В этом случае разделение производится на два класса состояний, т.е. выполняется дифференциальное диагностирование.

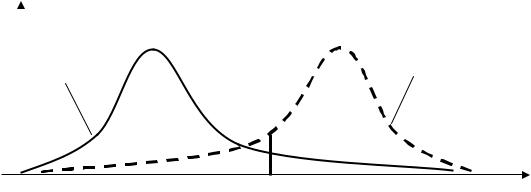
Рассмотрим плотность вероятности контролируемого параметра x для двух классов состояний системы ( D1 – исправное и D2 – дефектное ) (рис.2.20).

f(x/Di)	D1	D2
f(x/Di)		D2
f(x/D1)		f(x/D2)

x0	х

Рис. 2.20. Плотности вероятности параметра x для исправного D1 и дефектного D2

классов состояний

Из графика плотности вероятности (рис.2.20) следует правило принятия

решения о состоянии системы:
при	x < x0	x Î D1	ü
при	x > x0	x Î D2	ý	,	(2.35)
при	x > x0	x Î D2	þ

где х0 – граничное значение параметра для принятия решения.

Видно, что области исправного D1 и дефектного D2 состояний пересекаются.

Поэтому принципиально невозможно выбрать такое граничное значение xo , при котором правило (2.35) не давало бы ошибочных решений. В связи с этим

возникает задача оптимального выбора xo , которое бы давало наименьшее число ошибочных решений. Рассмотрим возможные ошибки при принятии решений.

Обозначим ошибку 1-го рода (''ложная тревога'') Н21 определили, что система находится в состоянии 2 – дефект есть, а на самом деле она находится в состоянии 1 – дефекта нет (исправное состояние), а ошибку 2-го рода (''пропуск дефекта'')

Н12.

Вероятность ложной тревоги равна произведению		вероятностей двух
событий:
α = P(H21) = P(D1 ) × P(x > x0 / D1) = P1 × òx∞0	f (x / D1)dx ,	(2.36)

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

где f(x/D1) – плотность распределения параметра x при условии, что имело место повреждение D1 ; P1 – априорная вероятность появления состояния D1 .

Вероятность пропуска дефекта

β = P(H12 ) = P(D2 ) × P(x < x0 / D2 ) = P2 × ò−x∞0 f (x / D2 )dx ,

(2.37)

где f(x/D2) – плотность вероятности параметра x при условии, что имело место повреждение D2 ; P2 – априорная вероятность появления состояния D2 . Для определения минимального (среднего) риска при принятии решения необходимо

составить матрицу потерь

С =	С11	С12	,	(2.38)
	С21	С22

где С11, С22 – затраты при правильном принятии решения о ''ложной тревоге'' или ''пропуске дефекта''; С12, С21 – затраты при неправильном принятии решения.

Тогда средний риск


R = C11 × P1 × ò−∞x0 f (x / D1 )dx + C21 × P1 × òx∞0	f (x / D1 )dx +
+ C12 × P2 × ò−∞x0 f (x / D2 )dx + C22 × P2 × òx∞0		f (x / D2 )dx.	(2.39)

Дифференцируя выражение (2.39) по х0 и приравнивая производные к нулю, получим следующее уравнение:


dR	= C × P × f (x		0	/ D )dx - C	21	× P × f (x	0	/ D	)dx +
	= C × P × f (x			/ D )dx - C		× P × f (x		/ D	)dx +
11		1		1		1		1
dx0
	+ C12 × P2 × f (x0 / D2 )dx - C22 × P2 × f (x0 / D2 )dx.									(2.40)

Из этого уравнения составим следующее соотношение:

		f (x0	/ D1 )		=	(C12 - C22 ) × P2		.	(2.41)

		f (x0 / D2 )				(C21 - C11 ) × P1
Откуда x Î D1		при		f ( x0 / D1 )			> (C12 - C22 ) × P2 ;		(2.42)

				f ( x0 / D2 ) (C21 - C11 ) × P1
x Î D2		при	f ( x0 / D1 )			< (C12 - C22 ) × P2 .			(2.43)

			f ( x0 / D2 ) (C21 - C11 ) × P1
Эти условия	справедливы при одномодальном ("одногорбом") распределении
значений параметра			диагностики x . В противном						случае для достижения
						57

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

минимума среднего риска R в точке x = xo					вторая производная должна быть
положительной	d 2 R	> 0 , что приводит к следующему условию:
	dxo2
		f ' (x0 / D1 )	<	(C12 - C22 ) × P2		,	(2.44)
		f '(x0 / D2 )		(C21 -	C11 ) × P1

т.е. для "двугорбых" распределений условие (2.44) должно проверяться в каждой точке экстремума.

Условие (2.42) соответствует x < xo , условие (2.43) - x > xo . Отношение

(C12 - C22 )× P2 = x

(C21 - C11 )× P1

представляет собой пороговое значение правдоподобия.

Рассмотрим пример. Предполагается, что плотность вероятностей признаков имеет вид гауссовой кривой. Задаемся величинами математических ожиданий

х1 и х2 , дисперсиями σ 12 , σ 22 и затратами С11, С12, С21, С22. Прологарифмировав левую и правую части выражения (2.41), определим

f (x0 / D1)

= -

[2x0 × (x2 - x1 ) + x12 - x22 ] =

f (x0 / D2)

σ12 × σ22

= ln

(C12

- C22) × P2

(2.45)

(C21 - C11) × P1

Решив это уравнение относительно xo , получим его значение:

x0 =

(x1 + x2 ) -

σ 2

× σ 2

C12

- C22 ù

× êln

+ ln

ú.

(2.46)

x2 - x1

C21

- C11 û

Рассмотрим числовой пример.

Пусть

имеем следующие исходные данные:

σ 2 = σ12

= σ 22 = 0,5;

x1 = 2,5;

x2 = 3,

вероятность

''ложной

тревоги'' P1= 0,1 , вероятность ''пропуска дефекта'' P2 = 0,009;

матрицу затрат

100

С= 1 0 .

Тогда, подставив исходные данные в (12), получим граничное значение параметра xo = 2,805.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

Метод наибольшего правдоподобия

Этот метод является частным случаем метода минимального риска. Правило

решения метода имеет вид

x Î D1 ,	если	f (x / D1 )	> 1,
		f (x / D2 )

x Î D2 ,		f (x / D1 )	(2.47)
	если		< 1.
		f (x / D2 )

Граничное значение диагностического параметра находят из условия

	f (x0 / D1) = f (x0 / D2 ).						(2.48)
Условия (2.41) и (2.48) совпадают, если принять
	(C12 - C22 ) × P2					= 1.	(2.49)
	(C21 - C11 ) × P1
В большинстве практических задач условные выигрыши (поощрения) для
правильных	решений не вводятся,					и тогда для	метода наибольшего
правдоподобия следует считать			×
		C12		P2	= 1.		(2.50)
		C21	×
				P1

Для задач по надежности ТС вероятность неисправного состояния представляет собой малую величину, но цена пропуска дефекта значительно больше цены ложной тревоги (С12 >>С21). Поэтому условие (2.50) дает решение, не требующее знаний точных оценок стоимости ошибок, и качественно отражает эти обстоятельства, т.е. P 2<< P1 , C 1`2>> C`21.

2.9.3.Нечеткие методы принятия решений

Впроцессе разработки диагностического обеспечения (ДО) сложных технических систем, например электронных систем (ЭС), как правило, отсутствует полная априорная статистическая информация об этих системах, как объектах диагностики. Аналогичная ситуация возникает при выявлении технического состояния сложных систем в процессе эксплуатации.

Вэтих случаях наиболее ценной и достоверной априорной информацией об объекте диагностирования является опыт экспертов (проектировщиков системы, инженерно-технического персонала, обслуживающего системы), который можно формализовать на основе концепций теории нечетких множеств.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

В п. 2.2 уже рассматривался один из подходов оценки технического состояния системы. Здесь будет рассматриваться метод принятия решения о состоянии системы на основе нечеткого интеграла [7, 19 ].

Пусть известны топология сложной цифровой системы G , допустимое

множество дефектов (состояний) Def = {dj} и допустимое множество контролируемых параметров (признаков, симптомов, контролируемых точек),

П = { п i }.

Предположим, что производится диагностический эксперимент над сложной системой, в результате которого по реакции контролируемых параметров (контрольных точек) пi Î П эксперт (эксперты) предполагает возможную область дефектов (состояний), представленную в форме нечеткого высказывания,

описываемого лингвистическим значением Dэ= {ПРИМЕРНАЯ ОБЛАСТЬ ВОЗМОЖНЫХ ДЕФЕКТОВ } , Dэ Def.

Процедура принятия решения на основе нечеткого интегрирования заключается в следующем.

Нечеткий интеграл представляет собой макси-минную композицию двух нечетких множеств. Первое множество может представлять апостериорную оценку какого-либо состояния, а второе множество дает априорную оценку элементов этого состояния. Первое множество является функцией принадлежности (ФП), а второе множество является нечеткой плотностью весов нечеткой меры элементов ФП.

Результатом нечеткого интегрирования является нечеткая мера апостериорного множества, которая может быть интерпретирована как "степень нечеткости", "степень важности", "степень уверенности", "степень доверия", "степень принадлежности", "степень предпочтения" или другими способами в зависимости от конкретной ситуации. Тогда распознавание ожидаемого типа

дефекта в ЦУ по результату диагностического эксперимента принимается из решения нечеткого интеграла

	d0 = arg òf μDэ (di )o gλ (×),		(2.51)
где òf	- знак нечеткого интеграла; Dэ – область возможных дефектов,
определяемых в результате испытания (эксперимента), описывается
убывающей функцией принадлежности μDэ(di); ο - знак композиции; gλ(×)			-
нечеткая	λ -мера упорядоченного	множества Fj = {d1, d2, …, dj } ,
которая определяется выражением [6 ]
	é	ù	(2.52)
	gλ (Fj ) = λ1 ê∏(1+ λ	× g(di )) -1ú	(2.52)
	ëi D	û

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

<<< < Предыдущая 1 2 3 4 56 / 116 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.04.2015469.9 Кб31Варианты по МФ.pdf
#
10.04.20155.27 Mб4ВВЕДЕНИЕ В ИГРЫ дидакти.pdf
#
24.11.2019434.28 Кб25Введение в предмет.docx
#
06.09.201979.36 Кб2вводные слова и предложения. Анна Каренина.doc
#
15.08.2019185.34 Кб2Вентиляция.doc
#
10.04.2015796.03 Кб59Вешкурцев- Бычков АСКиД РЭС.pdf
#
09.04.2015127.49 Кб11Виды и типы религии, секты.doc
#
16.09.20195.26 Mб22ВИХРЕТОКОВЫЙ КОНТРОЛЬ(Часть2).doc
#
15.03.2016380.08 Кб5ВКР. Специальность Менеджмент организации. Базилевич С.В., Беляева Е.Р..pdf
#
15.03.201620.42 Mб119ВЛ11К 2010г..doc
#
15.03.201620.15 Mб138ВЛ11К РЭ.pdf