Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Омский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Вешкурцев- Бычков АСКиД РЭС

.pdf

Скачиваний:

Добавлен:

10.04.2015

Размер:

796.03 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 114 5 6 7 8 9 10 11 > Следующая >>>

где	К( jω) =	bm (jω) m + bm-1 ( jω )m-1 + … + b1( jω)1 + b0
							.

		an( jω )n+ an-1 ( jω)n-1 + … + a1( jω )1 + a0
Например, для	LC–цепи частотный коэффициент			передачи определяется
выражением [14]	1

	К( jω) =				,

			( 1 - ω2 L C ) + j ωRC
а амплитудно-частотная характеристика (АЧХ) −
	1
	\| К( jω )\| =					.

			[ ( 1 − ω2 LC )2 +	ω2 R2 C2 ]1/2

Вышерассмотренные операторы функционирования электронных устройств описывают линейные аналоговые стационарные системы, на которых и остановимся. Операторы других видов более подробно рассматриваются в специальной литературе [ 15 ].

2.8.3. Математическая модель объекта контроля и диагностики

Рассмотрим классификацию систем ( рис. 2.4). Под объектом контроля и диагностики (ОКД) будем понимать некую техническую систему (ТС), являющуюся элементом системы технической диагностики (СТД), которая метрологически аттестована. Следовательно, СТД имеет технический паспорт при надежных и работоспособных всех ее элементах, в том числе и ТС. Тогда

отказ любого элемента системы или изменения его состояния сразу же сказывается на показателях технического паспорта СТД. Таким образом,

техническая система, включенная в общую	конфигурацию СТД, может
обеспечить самодиагностику.

Электронные технические системы в зависимости от использования элементной базы подразделяются на три основных класса: аналоговые, дискретные (цифровые) и гибридные (комбинированные) [16-18]. В связи с этим, как уже отмечалось ранее, математические модели ОКД соответственно подразделяются на аналоговые, цифровые и комбинированные, которые, в свою очередь классифицируются на детерминированные, стохастические и нечеткие

(fuzzy) модели [19] .
При разработке алгоритмов технического диагностирования	используются
математические модели как исправных состояний ОКД, так и	неисправных их

состояний. Поэтому математические модели радиоэлектронных систем, как ОКД,

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

по сложности существенно отличаются от моделей РЭС в традиционном (исправном) представлении, т. к. модели ОКД многопараметрические. В

обобщенном виде математическую модель ОКД можно представить в виде системы множеств

Mокд = á C, K, P, Def, Sп, Sd, Pd, Ф, L ñ ,

где бЧЧЧс - означает систему функциональных зависимостей; C - структура ОКД, которая определяется требуемой глубиной диагностики РЭС; K- множество контрольных точек; P - множество параметров (признаков) диагностирования, P= {п}; Def- множество возможных дефектов, Def={d}; Sп- подсистема множеств исправных состояний РЭС , Sп={sj} , sj= {rj1 ,rj2 ,…, rji} ,rji - элементарные априорные дискретные признаки (реакции); Sd - подсистема множеств неисправных состояний, порождаемые дефектами d, Sd={sj},

SпÇSd¹Æ; Pd - априорная статистика распределения. дефектов в ОКД ; Ф -

множество операторов функционирования или функций переходов системы из одного в другое состояние, отражающих механизм изменения состояния системы под воздействием внутренних и внешних возмущений; L – оператор выходов,

описывающий механизм формирования выходного сигнала как реакции ОКД на внутренние и внешние возмущения.

Операторы Ф и L реализуются отображениями
Ф : Х ´ (Sп È Sd ) ®(Sп È Sd )
L : Х ´ (Sп È Sd ) ® Y	,

где Х - множество входных сигналов; Y – множество выходных сигналов.

2.8.4. Цифровые модели объекта диагностики

Различают функциональные и структурные модели цифровых устройств (ЦУ). В функциональных моделях отсутствуют сведения о внутренней структуре устройства. Функциональной моделью комбинационного ЦУ может служить, например, таблица истинности или система булевых функций, соответствующих выходам устройства, причем аргументами функций являются входные сигналы устройства. Функциональной моделью ЦУ с памятью обычно служит конечный автомат [16].

Структурной моделью ЦУ является, как правило, логическая сеть, которая задается перечислением входов, выходов элементов ЦУ и связями между ними. Различные модели цифровых устройств подробно рассмотрены в [16, 20 ]. Для

решения задач технической диагностики моделируются не только исправные

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

состояния ЦУ, но и неисправные. При моделировании ЦУ как ОД чаще всего рассматривают класс одиночных константных неисправностей, тождественно равных единице ("1") или нулю ("0") , с учетом того, что многие полученные при

этом результаты можно будет распространить на другие классы неисправностей (например, короткое замыкание, обрыв, перепутывание контактов, изменение функций и т.д.) [16, 20].

Комбинационные ЦУ

В комбинационных логических схемах сигнал на выходе зависит только от сигнала на входе в данный момент.

Пусть имеется устройство с k входами и q выходами

x1	Комбинацион-	y1
x2	ное логическое	y2
xk	устройство	yq

Рис.2.12. Комбинационное ЦУ

Тогда в общем виде математическая модель комбинационного логического устройства имеет вид системы

y1 = f1 (x1 , x2 ,..., xk )	ü
y2 = f2 (x1 , x2 ,..., xk )	ïï	,
	ý	,
::::::::::::::::::::::::ï
yq = fq (x1 , x2 ,..., xk )	þï

при этом xk {0,1}, yq {0,1}.

Функции f1... fq , описывающие только комбинационные устройства, получили название булевых функций (БФ). Максимальное число входных воздействий,

составляющих k аргументов БФ,			равно 2k ,	которые можно	определить как
множество	входных состояний	Sвх	= {si }12k	с разрядностью	k.	Аналогично
множество	выходных состояний	Qвых = {qi }12q		с разрядностью		q. При этом

si , qi {0,1}. Например, пусть логическая схема ( рис. 2.13) имеет четыре входа и один выход: si = (x1 , x2 , x1 , x2 ). Булева функция имеет вид

y = (x1 È x2 )Ç (x1 È x2 )= x1x2 È x1x2

x1	1
x1	1
x2			(x1 È x2 ) Ç (x1 È x2 )


x1		&
		&


	1

Рис. 2.13. Логическая схема

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

Математическая модель комбинационной схемы может быть задана также таблицей истинности. Например, табл.2.1 для логической схемы "И" .

		Таблица 2.1
x1	x2		y
0	0		0
0	1		0
1	0		0
1	1		1

Модели цифровых устройств с памятью

Обобщенная модель цифрового устройства с памятью представляется конечным автоматом, который задается системой множеств

A = áX, Z, V,υ0 ,δ , λñ ,

где Х – конечное множество входных состояний (воздействий) или входной алфавит; Z – конечное множество выходных состояний (выходной алфавит реакций); V – конечное множество внутренних состояний (алфавит состояний) с

начальным состоянием uo; δ – функция переходов автомата,									δ: X × V → V ;
λ – функция выходов автомата, λ:				X × V → Z .
	Входной алфавит Х представляется					множеством			двоичных	векторов
x	= {x1 , x2 ,..., xn }, где n – число входных переменных или входов ЦУ.
	Выходной	алфавит	Z	–		множество		двоичных		векторов
z	= {z1 , z2 ,..., zm } , где m – число выходных переменных ЦУ (выходов ЦУ).
	Алфавит состояний V – множество двоичных векторов υ = {υ11 , υ2 ,..., υ p },
где р – число внутренних переменных автомата.
	Работа конечного автомата представляется в виде модели Миля									[20] и
описывается системой булевых функций
		r				r
		υ(t +1) =δ [υ(t), x(t)];ü
		r		r	r		ý
		z	(t) = λ[υ		(t), x(t)]		þ
или в виде модели Мура [20]
		υ(t +1)=δ[υ(t), x(t)];ü
		r		r	(t)].		ý
		z	(t)= λ[υ		(t)].		þ

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

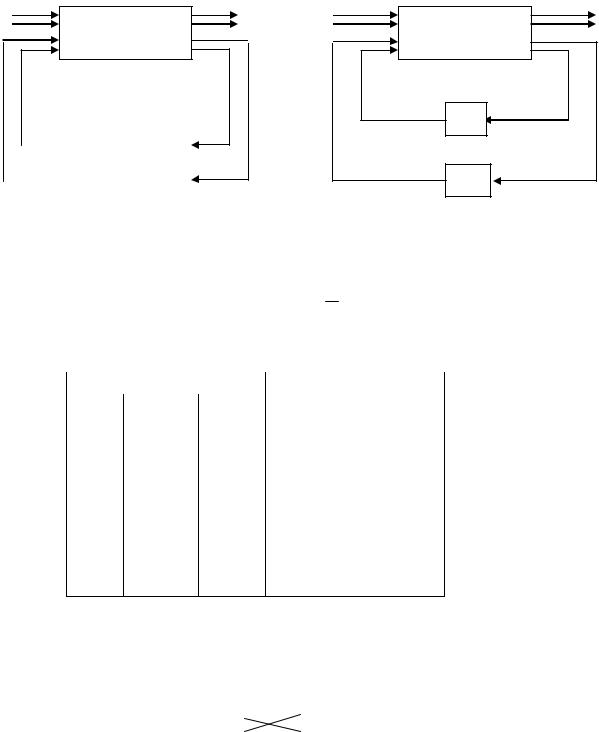
Структурные схемы синхронного и асинхронного автоматов представлены на рис. 2.14 и 2.15 соответственно.

x1	Комбинационная	Z1
xn		zm
	часть

y1		y1
	Запоминающая
	Запоминающая
	часть

yP		yP
yP		yP

Рис.2.14. Синхронный автомат

x1	Комбинационная	Z1
xn	Комбинационная	zm
	часть
	1	y1
	y1	y1
	P	yP
	yP	yP
	Рис.2.15. Асинхронный автомат

В качестве примера рассмотрим автомат на основе синхронного триггера типа RS ( рис. 2.16), который характеризуется уравнением

Qn +1 = S + RQn

и таблицей истинности (табл.2.2).

			Таблица 2.2
	t = n		t = n + 1
S	R	Qn	Qn+1
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	×
1	1	1	×

В табл. 2.2 знак × определяет неопределенное состояние триггера.

S		Q
S	&
R	&






	&
	&	Q
		Q

Рис. 2.16 . Триггер типа RS

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

Рассмотрим примеры построения диагностических тестов для ЦУ на основе метода булевой производной [ 12, 16].

Построение тестовых наборов методом булевой производной

Этот метод построения тестовых наборов относится к детерминированной генерации тестов при условии, что дефекты ЦУ проявляются в виде константных неисправностей типа ''0'' и ''1''.

Булевой производной функции f (x)= f (x1 ,x2 ,..., xn ) по xi называется функция

df (x ) = f (x1 ,x 2 ,..., xi ,..., xn ) Å f (x1 ,x 2 ,..., xi ,..., xn ), dx i

где Å – суммирование по модулю 2.

Булева производная также может быть вычислена по следующей формуле:

df (x ) = f (x 1 , x 2 ,..., 0 ,...,		x n )	Å f (x 1 , x 2 ,..., 1,..., x n )
dx i
Тестом для поиска неисправностей xi			0 и xi 1 являются значения логических
переменных, при которых xi	df (x)	= 1 ,	xi	df (x)	= 1.

	dx i
				dxi

Вышеприведенные формулы распространяются и на внутренние переменные. Приведем примеры построения тестов методом булевой производной.

Пример 1. Пусть задана схема.

x1
x1	&	1	f (x)=x1x2	+ x2
x2	&	1


x3

Найти тесты неисправностей x1 0 и x1 1 . Тогда булева производная имеет вид

df (x) = (1× x2 + x3 )Å (0 × x2 + x3 )= (x2 + x3 )Å x3 = (x2 + x3 )x3 + (x2 x3 )x3 = x2 x3 .

dx1

Тест для x1 0 определяется из уравнения (условия)

x1	df (x)	= 1, т.е. x x		x		= 1 (x = 1; x		= 0).
	dxi		2		3		3
		1				1

Тест для x1 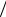1 определяется из уравнения (условия)

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

x1	d ( f ) = x1 x2 x3 = 1 (x = 0; x =1;x = 0).
	dx1	1	2	3

Пример 2. Пусть задана следующая схема.

	f (x)	= x1 x2 + x1 x2


&
&

Найти тесты неисправностей x2 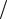0 и x2 1. Находим булеву производную

df (x) = (x1 × 1 + x1 × 0) Å (x1 × 0 + x1 × 1) = 0 . dx2

Это означает, что

f (x) не зависит от x2 .

Следовательно, могут возникать случаи,

когда вход

схемы методом булевой

производной не проверяется.

Пример 3. Дана схема.

f(x)

Найти тест неисправности

y2 0 . Выразим f(x)

через внутренние переменные

схемы: f (x)

. Затем находим булеву производную

y1 + y2

= (y1 + 0) Å (y1 + 1) = y1 Å 0 = y1 = x1 + x2 .

Тест для y2

0 найдем из условия у

= 1,

dy2

т.е.

(x3 + x4 )(x1 + x2 )= x3 x4 (x1 + x2 )= x3 x4 x1 + x3 x4 x2 =1.

Следовательно,

тестом

является

набор

x1 = 1; x2 = 0; x4 = 0

или

x2 = 1; x3 = 0; x4 = 0 .

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

В тех случаях, когда в схеме имеются разветвления, для вычисления полного

теста схемы необходимо найти булеву производную для всех разветвлений по переменной, обозначающей разветвленную линию. В связи с этим вводится понятие булевой производной по переменной xi для пути Рk .

Пусть в схеме имеется путь Pk

= {xi , y j , yi , ym , f }.

Булева производная для этой схемы имеет вид

df (Рk )

dym

dyi

dxi

dym

dyi

dy j

Пример 4.

Дана схема.

f (x)= x1 x2 x3 + x1 x2 x3

Для вычисления тестов неисправностей линий 1 и 8 найдем булевы производные f (x) по x1 для путей

Р1 = (x1 , y4 , y7 , f ); P8 = (x1 , y6 , y8 , f ).

				df (p1 )			=			df			dy7			dy4			.
				dx			=			dy									.
				dx						dy	7		dy	4		dx
						1					7			4				1
df						f (x)= y7 + y8 .
df	= x		= x			+ x			+ x				= x			x		+ x x			+ x		.
	= x	8	= x		5	+ x		6	+ x			3	= x		2	x	3	+ x x		3	+ x	3	.
dy7		8			5			6				3			2		3	1		3		3
dy7

y7 = x2 y4 y5 .

dy = x2 y5 = x2 (x2 + x3 )= x2 x3 .

dy4

y		=			.	dy4	= x		.
	4		x x	2				2

		1				dx1

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

df (Р1 )

= (x2 x3 + x1 x3 + x3 )(x2 x3 ) x2 = x2 x3 .

dx1

Тесты неисправностей 1 0 , 1 1 находятся из условий

x 1

df ( P )

= 1; x1

df ( P )

= 1 .

dx 1

Тест 1 0

x2 x3 →110 . Тест 1 1

x1 x2

x3 → 010.

Аналогично находятся тесты для неисправностей 8 0 , 8 1 .

df (p8 )

dy8

dy6

= x2 x3

dy8

dx1

dy6

dx1

Тест 8 0

x1 x2

x3 →101. Тест 8 1 x1 x2

x3 → 0 01.

Метод булевой производной для ОКД с памятью

При вычислении тестов для ОКД с памятью необходимо:

1)составить множество булевых функций, описывающих ОКД с памятью;

2)выбрать одну из выходных функций z j (j =1,m). Выбрать путь Рk ,

начинающийся от входа

xi (i =

)

и заканчивающийся z j , и вычислить булеву

1,n

производную z j по переменной

xi для этого пути

dz j (Рk )

;

dxi

3) выбрать по возможности терм, удовлетворяющий условиям

dz j (Рk )

¹ 0 и x

dz j (Рk )

¹ 0 ,

dxi

если dz j (Рk ) содержит более одного терма. dxi

4) проанализировать терм, выбранный на предыдущем шаге, если он содержит одну и более переменных обратной связи, требующих предварительной установки состояния ОКД , то найти соответствующий установочный набор.

Если терм не содержит переменных обратной связи, то установочного набора не требуется. Тесты вычисляются из условия равенства единице результата логического умножения xi и xi на выбранный на шаге 3 терм.

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

Рассмотрим схему триггера с булевыми функциями F = x1x2 + x1 x2f + x2f;

= x1x2 + x1

+ x2

, где f – переменная обратной связи.

				_
&		f	&
&			&
3	y2		4		F


				y3
				y3

В установившемся режиме f

= F .

Выберем путь P1 = (x1, y1, F)

и найдем булеву производную

dF(P1 )

öæ

dy1

÷ç

ç dy

÷ç dx

÷; F = y1 × y2 .

øè

dF =1Å y3

= y3 .

dy1

y3 =

= y2 +

;

y2 f

y2 =

; y2 = y1x2 ;

y1x

y3 = y1 x2 + f; y1 =

= x1 x2 +

x1 x2

= x1 x2 +

;

dy1 =1Å x2 = x2 .

dy1

dx1

dF(P1 )

= (x1 x2 +

)x2 = x1 x2 + x2

dx1

Это выражение определяет две пары тестовых наборов: x1x2 x1 ,

x1x2 x1 и

x1, x2

x1 , при этом x1x2 x1 = 0 . Тест x1x2

обеспечивает тестирование только

неисправности x1

/ 1. Поэтому

необходимо

выбрать вторую

пару

тестовых

наборов с соблюдением условия

= 1,

при этом

= 1.

Установочный

набор для

= 1

определяется из равенства

= x1 x2 + x1

+ x2

Из трех

возможных термов

(x1 x2 , x1f и x2f )

PDF создан испытательной версией pdfFactory Pro www.pdffactory.com

<<< < Предыдущая 1 2 34 / 114 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.04.2015469.9 Кб31Варианты по МФ.pdf
#
10.04.20155.27 Mб4ВВЕДЕНИЕ В ИГРЫ дидакти.pdf
#
24.11.2019434.28 Кб25Введение в предмет.docx
#
06.09.201979.36 Кб2вводные слова и предложения. Анна Каренина.doc
#
15.08.2019185.34 Кб2Вентиляция.doc
#
10.04.2015796.03 Кб59Вешкурцев- Бычков АСКиД РЭС.pdf
#
09.04.2015127.49 Кб11Виды и типы религии, секты.doc
#
16.09.20195.26 Mб22ВИХРЕТОКОВЫЙ КОНТРОЛЬ(Часть2).doc
#
15.03.2016380.08 Кб5ВКР. Специальность Менеджмент организации. Базилевич С.В., Беляева Е.Р..pdf
#
15.03.201620.42 Mб119ВЛ11К 2010г..doc
#
15.03.201620.15 Mб138ВЛ11К РЭ.pdf