3.1.3. Оценка результирующей систематической погрешности и внесение поправок

После анализа схемы измерения и вычисления систематических погрешностей имеется ряд значений _сj,j= 1k. Каждая из_сjимеет свою природу возникновения, а также свои значение и знак. Результирующая систематическая погрешность вычисляется по формуле:

, (3.9)

где k– количество вычисленных неисключенных погрешностей.

Затем вычисляют поправку

. (3.10)

Если , т. е. не зависит от времени, то ее можно внести в среднее значение:

. (3.11)

В случае, когда является функцией времени, поправку вводят в каждый результат наблюдения:

, (3.12)

а затем определяют

. (3.13)

Внеся поправку в результат наблюдения, получают несмещенное значение измеряемой величины, которое является неокончательным, поскольку еще не учтены погрешности приборов и модельные составляющие погрешности измерения (погрешности сопротивления, емкости, индуктивности, температуры, источников питания и т. д.), т. е. все то, что относится к неисключенным остаткам систематической погрешности.

3.1.4. Неисключенные остатки систематической погрешности

Неисключенные остатки (НО) систематической погрешности () – это та ее часть, которая остается после оценки и устранения этой погрешности (рис. 3.3).

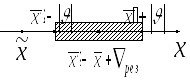
Рис. 3.3. Смещенный интервал неисключенных остатков

Исследование неисключенных остатков предполагает выполнение следующей работы:

• анализ источников возникновения;

• оценка _i(i= 1, 2, ...,k) по каждому источнику возникновения;

• оценка результирующей составляющей неисключенных остатков систематической погрешности.

Особенность исследования неисключенных остатков, представляющих собой составляющую систематической погрешности, заключается в том, что значения _iнедетерминированы, т. е. представляют собой случайную величину, которую можно охарактеризовать средним квадратическим отклонением (СКО).

Тогда _резсоответствует свое результирующее СКО:

, (3.14)

где b_i– функция влияния_iна конечный результат.

Если влияние компонентов на конечный результат неизвестно, то вводится гипотеза об одинаковом влиянии каждого компонента (b_i= 1).

В том случае, когда закон изменения каждого компонента неизвестен и нет возможности определить хотя бы его вид, вводится гипотеза о том, что отдельные компоненты неисключенных остатков распределены равномерно. Реализация этой гипотезы позволяет для каждого _iвыбрать границы_i, для_рез–_рез:

, (3.15)

где k– поправочный коэффициент, зависящий от числа компонентов и доверительной вероятности.

Зависимость kот числа компонентов слабая. Значение коэффициентаkпри доверительной вероятностиРприведены в табл. 3.1.

Таблица3.1

Значения коэффициента kв зависимости от числа слагаемых и доверительной вероятностиP

Число слагаемых n	Значение погрешности kпри доверительной вероятностиР
	0,9	0,95	0,99	0,9973
2	0,97	1,10	1,27	1,34
3	0,96	1,12	1,37	1,50
4	0,96	1,12	1,41	1,58
5	0,96	1,12	1,42	1,61
6	0,96	1,12	1,42	1,64
…	…	…	…	…
	0,95	1,13	1,49	1,73

Результат измерения при доверительной вероятности Р записывается в следующем виде:

. (3.16)