2.4. Распределение Бозе-Эйнштейна. Теоретические сведения

Частицы, которые описываются симметричной волновой функцией (2.12), имеют целый спин и называются бозонами. Бозонами являются все частицы-переносчики взаимодействия: фотон (спин ), гравитон (спин ), -мезоны (спин ). Числа заполнения квантовых состояний при симметричных волновых функциях ничем не ограничены и могут иметь произвольные значения. Основным квантово-статистическим свойством бозонов является то, что вероятность появления бозона в некотором квантовом состоянии тем больше, чем больше таких же бозонов уже находится в этом состоянии. ИГ, состоящий из бозонов и описываемый симметричными относительно перестановок частиц волновыми функциями (2.12), называется идеальным бозе-газом.

Среднее число бозонов на уровне с энергией вычисляется по формуле:

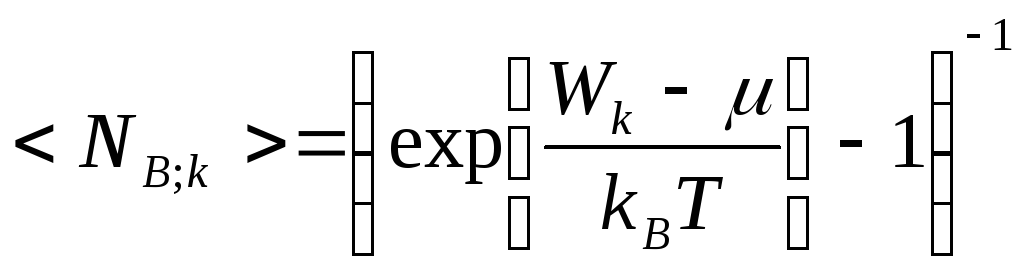
Формула (2.21) определяет распределение частиц идеального бозе-газа по энергетическим уровням и называется распределением Бозе-Эйнштейна. Химический потенциал системы бозонов .

На рис. 2.5 показано распределение массивных бозонов по уровням энергии в различных областях значений энергии.

Рис. 2.5, а отвечает идеальному случаю: при К все бозоны расположены на самом нижнем энергетическом уровне – наблюдается явление конденсации Бозе-Эйнштейна.

При увеличении температуры часть бозонов переходит в более высокие энергетические состояния за счет теплового возбуждения.

Распределение бозонов, имеющих при К небольшие значения энергии, показано на рис. 2.5, б.

При больших значениях энергии частиц в правой части выражения (2.21) единицей можно пренебречь по сравнению с экспонентой:, а распределение Бозе-Эйнштейна (2.21) переходит в распределение Максвелла-Больцмана (рис. 2.5, в, г), определяемое при заданной температуре функцией:

,

(число бозонов, имеющих высокие энергии, очень мало по сравнению с числом возможных состояний) причем множитель является нормировочным (сравните с формулами (1.4) – (1.7)) и определяется условием нормировки.

Для системы бозе-газа безмассовых частиц, например, фотонов⁷ или фононов, химический потенциал равен нулю, так как в систему, содержащую таких частиц, всегда можно добавить-ую частицу с исчезающе малой (в пределе – нулевой) энергией, поэтому формула (2.21) для распределения Бозе-Эйнштейна принимает вид:

.

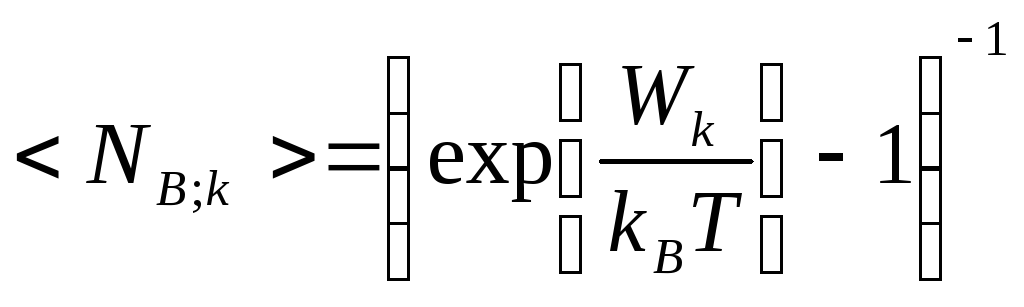Как следует из (2.22) при K газ безмассовых бозонов перестает существовать [1].

2.5. Тепловое излучение. Применение распределения Бозе-Эйнштейна к тепловому излучению. Теоретические сведения.

Все нагретые тела испускают электромагнитное излучение (ЭМИ). Средняя мощность излучения, испускаемого с единицы поверхности тела, называется интенсивностью излучения (энергетической светимостью). Максимум интенсивности в спектре равновесного теплового излучения нагретого до температуры тела приходится приближенно на волну длиной, определяемой законом смещения Вина:

,

где константа = 2,9 мм·К - постоянная Вина.

Абсолютно черное тело (АЧТ) – (идеальное) тело, полностью поглощающее весь падающий на него поток ЭМИ. Моделью АЧТ является полое тело с абсолютно непрозрачными (непропускающими ЭМИ) стенками и очень маленьким отверстием, через которое ЭМИ попадает в эту полость, и, отражаясь от стенок, образует трехмерные стоячие электромагнитные волны (ЭМВ). ЭМИ находится в термодинамическом равновесии со стенками полости, то есть температуры вещества и поля одинаковы. Поэтому тепловое излучение АЧТ является равновесным.

Вследствие закона излучения Кирхгофа [5,7] тело, которое при данной температуре сильнее поглощает ЭМИ, должно интенсивнее излучать. Поэтому наибольшей интенсивностью теплового излучения обладает АЧТ. Интенсивность ЭМИ АЧТ можно вычислить по закону Стефана-Больцмана:

,

где = 56,7 нВт/(м² K⁴) - постоянная Стефана-Больцмана.

а б в

г

Рис. 2.5. Распределение массивных бозонов в различных областях значений энергии: а - при К все бозоны расположены на самом нижнем энергетическом уровне; б - при К и небольших значениях энергии; в, г - приК и больших значениях энергии

Распределение энергии излучения АЧТ по спектру при заданной температуре рассчитывается по закону излучения Планка, полученному им на основе экспериментальных данных:

,

где величина -испускательная способность АЧТ - энергия излучения, испускаемого единицей площади поверхности тела в единицу времени, отнесенная к единичному интервалу частот.

Закон излучения Планка теоретически был получен А. Эйнштейном при изучении квантовых переходов атомов, находящихся в равновесии с ЭМИ. Каждой стоячей волне можно сопоставить колеблющейся с такой же частотой линейный гармонический осциллятор (ЛГО). При переходе ЛГО в состояние с меньшей энергий, в виде кванта энергии ЭМВ излучается фотон. Чем выше энергия ЭМВ с данной частотой, тем больше число фотонов такой частоты в полости, и, следовательно, тем большее число таких фотонов излучается. Так как весь спектр частот ЭМИ в полости занимает область много большую, чем интервал между соседними частотами, его можно считать непрерывным. В таком представлении полость нагретого излучающего тела рассматривается как объем, заполненный газом фотонов различных типов (различной энергии). Количество фотонов в полости не фиксировано, они могут рождаться и умирать. Кроме того, фотоны не локализованы: нельзя сказать, в каком месте полости находится каждый фотон.

Фотоны обладают энергией и спином, равным единице. Импульс безмассового фотона, движущегося в вакууме со скоростью света, .Однако, каждой частоте отвечает не три (), а два типа фотонов, так как вдоль заданного направления могут распространяться две поперечных ЭМВ, поляризованных во взаимно перпендикулярных направлениях. Поэтому можно считать, что одному фотону отвечает двавозможных спиновых состояния. Учитывая это и подставив в равенство (2.10) выражение для импульса фотона, определим концентрацию состояний ⁸ с частотами в диапазоне от до [5]:

.

В формуле (2.23) легко распознается распределение (2.22), чего и следовало ожидать, принимая во внимание, что фотоны, из которых состоит ЭМИ, относятся к классу безмассовых бозонов и подчиняются статистике Бозе-Эйнштейна при равном нулю химическом потенциале:

.

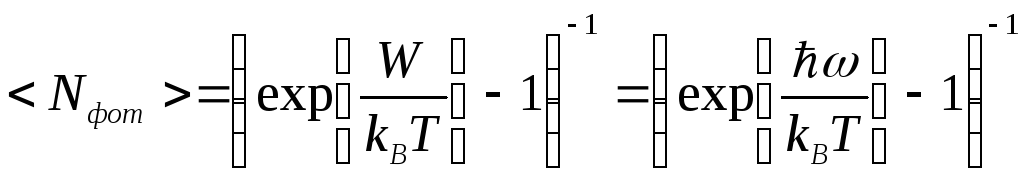Формула (2.25) позволяет найти среднее число фотонов с энергией в полости при температуре . Чем выше температура, тем больше число фотонов. Чем фотоны более высокочастотные, тем меньше их возникает при данной температуре.

В соответствии с равенством (2.11) концентрация фотонов с частотами в диапазоне от до в излучении АЧТ, получится, если умножить концентрацию состояний вблизи частоты (2.24) на среднее число фотонов, находящихся в данном состоянии, то есть обладающих энергией, отвечающей данной частоте (2.25):

.

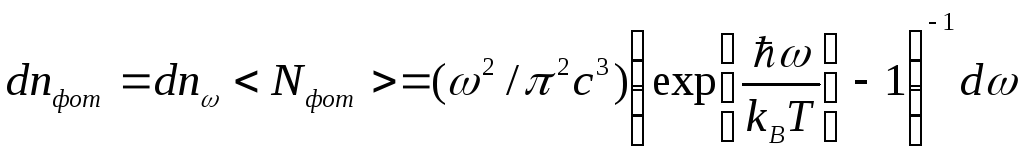Среднюю энергию излучения с частотой можно рассматривать как сумму энергий фотонов с энергией , то есть как произведение энергии одного фотона на среднее число фотонов, обладающих данной энергией (2.25):

.

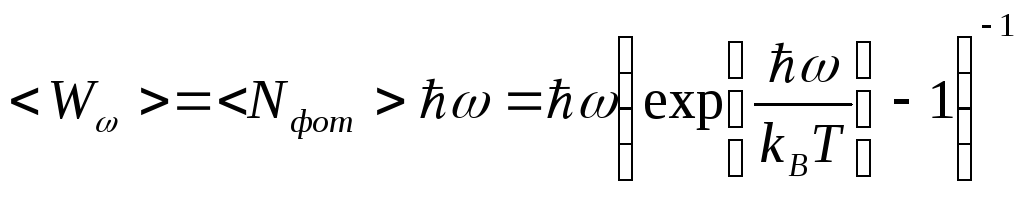Объемная плотность энергии излучения в диапазоне частот от до определяется произведением концентрации соответствующих фотонов (2.26) на энергию одного фотона:

,

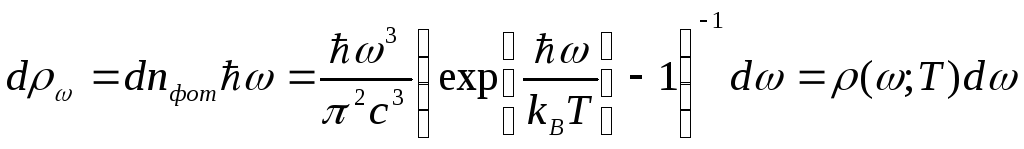где объемная плотность излучения АЧТ, отнесенная к единичному интервалу частот

,

связана с испускательной способностью АЧТ соотношением: . Формула (2.27), как и (2.23), называется законом излучения Планка.