1.2. Распределение Максвелла. Теоретические сведения

Найдем функцию распределения для импульса частицы ИГ.

Интегралы по компонентам импульса в правой части равенства (1.6) разделяются и вычисляются с помощью табличного интеграла [2]:

.

Тройное интегрирование в условии нормировки (вероятность найти частицу хоть с каким-нибудь импульсом равна единице) дает значение, а формула (1.6) принимает вид:

.

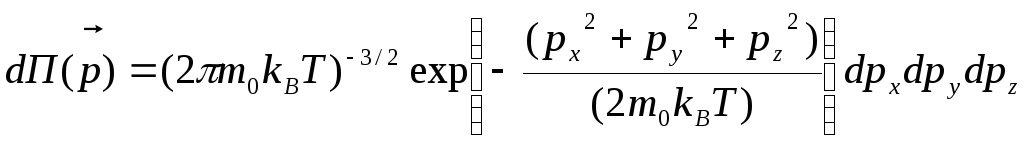Используя выражение , можно перейти от импульсов к скоростям и получить распределение вероятности для скорости:

.

Функция распределения по скоростям классических нерелятивистских частиц физической системы, находящейся в статистическом равновесии, задаваемая формулой

,

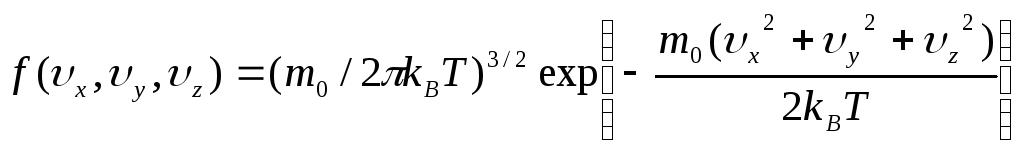называется распределением Максвелла по проекциям скорости. Распределение Максвелла (1.11) определяет вероятное число частиц ИГ, компоненты скоростей которых лежат в интервалах от до , от до , от до .

Отсюда можно найти функцию распределения для модуля скорости частиц ИГ, которая называется распределением Максвелла по модулю скорости и задается формулой:

.

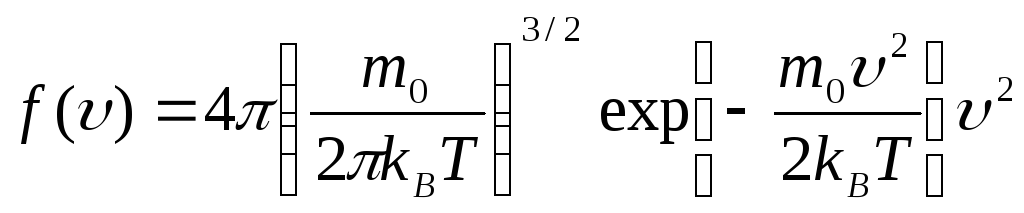Она позволяет определить число молекул в объеме , занимаемом ИГ, модуль скорости которых лежит в интервале значений от до :

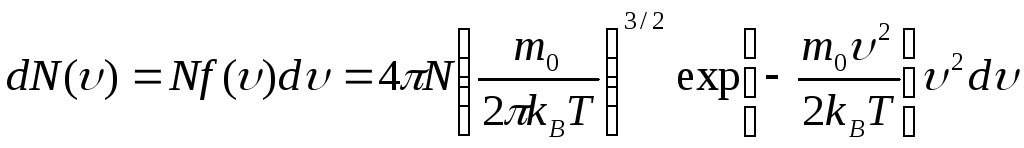
где – полное число частиц ИГ.

Чтобы найти среднее число частиц , модули скоростей которых лежат в интервале значений от до , нужно проинтегрировать функцию (1.13) в заданных пределах¹:

.

Вероятность обнаружения, или, другими словами, относительное число частиц ИГ, модуль скорости которых лежит в интервале значений от до , равна:

.

Вероятность обнаружения (относительное число) частиц ИГ, модуль скорости которых принимает значение в интервале от до , находится по формуле:

.

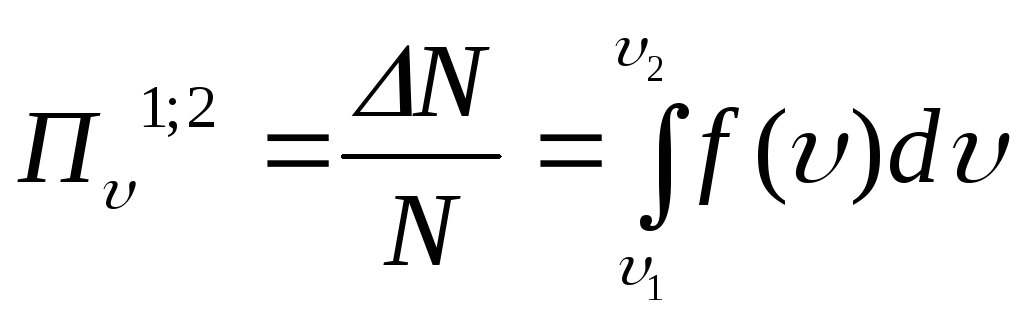Значение модуля скорости, при котором распределение Максвелла (1.12) максимально, называется наиболее вероятной скоростью. Наиболее вероятная скорость .

С помощью распределения Максвелла можно найти среднее значение любой функции, зависящей от скорости частицы. Например, среднее значение модуля скорости и среднеквадратичная скорость соответственно равны: и .

Для решения задач на распределение Максвелла в дополнение к интегралу (1.8) понадобятся следующие интегралы [2]:

; ;.

Кроме того, с учетом свойства монотонности подынтегральной функции значение интеграла (1.14) (и подобных ему) при близких значениях пределов интегрирования и () достаточно точно вычисляется по приближенной формуле: , где – значение функции распределения Максвелла (1.12) при .

1.3. Распределение Максвелла. Задачи для самостоятельного решения

1(1). При н. у. в сосуде объемом 5 л находится аргон. Вычислить количество молекул аргона, скорости которых лежат в интервале от 300 до 310 м/с.

2(2). Найти отношение вероятностей обнаружения молекул азота и кислорода со скоростями, отличающимися на 20 м/с от первой космической скорости при температуре 27 C.

3(2). Найти вероятность того, что молекула кислорода при 297 K имеет скорость, отличающуюся от не более, чем на 1 %.

4(2). У какой части молекул водорода при температуре 127 C скорости движения отличаются от наиболее вероятной не более, чем на 2 %?

5(1). Найти отношение вероятности обнаружить молекулы аргона со скоростями, отличающимися на 1 м/с от наиболее вероятной при температуре 200 K, к вероятности обнаружить эти же молекулы со скоростями, отличающимися на 1 м/с от наиболее вероятной при температуре 300 K.

6(2). Определить относительное число молекул азота, модуль скорости которых при 24 C меньше на 1 %.

7(2). Вычислить долю молекул ксенона, находящихся при температуре -73 C, скорости которых лежат в интервале от 100 до 110 м/с.

8(2). Во сколько раз для молекул аргона при температуре 400 C вероятность иметь скорость, отличающуюся на 15 м/с от первой космической скорости, больше, чем вероятность иметь скорость, отличающуюся на 15 м/с от второй космической скорости?

9(2). Во сколько раз относительное число молекул кислорода больше относительного числа при 280 К, если модуль скорости и тех, и других частиц принадлежит интервалу: а) от 19,8 до 20,2 м/с; б) от 1980 до 2020 м/с?

10(3). Используя распределение Максвелла, получить выражение для наиболее вероятной скорости частиц ИГ.

11(3). Используя распределение Максвелла, получить выражение для средней кинетической энергии поступательного движения и среднеквадратичной скорости частиц ИГ.

12(3). Используя распределение Максвелла, получить выражение для средней скорости частиц ИГ.