17

3.Информационные ресурсы дисциплины

3.1.Библиографический список

Основной:

1.Кремер, Н. Ш. Эконометрика / Н. Ш. Кремер, Б. А. Путко. – М.: ЮНИТИ-

ДАНА, 2002, 2005. – 311 с.

Дополнительный:

2.Доугерти, К. Введение в эконометрику: учебник: пер. с англ. / К. Доугерти. – М.: ИНФРА – М, 2004. – 418 с.

3.Эконометрика / под ред. И. И. Елисеевой. – М.: Финансы и статистика, 2005. – 576 с.

4.Практикум по эконометрике / под ред. И. И. Елисеевой. – М.: Финансы и статистика, 2005. – 192 с.

3.2.Опорный конспект*

Введение

Эконометрика – это наука, которая устанавливает и исследует количественные закономерности и взаимозависимости в экономике на основе анализа реальных статистических данных.

Эконометрика базируется на математической статистике и экономической теории. Экономическая теория выявила и исследовала большое число устоявшихся связей между различными показателями. Эти закономерности сформулированы качественно. Например, экономическая теория утверждает, что спрос на товар с ростом его цены убывает, но при этом не отвечает на вопрос, как быстро. Эконометрика с помощью математико-статистических методов в каждом конкретном случае придает количественное выражение общим закономерностям.

Задачей эконометрики является построение эконометрических моделей и оценивание их параметров, проверка гипотез о свойствах экономических показателей и формах их связи.

* Нумерация разделов, параграфов, формул, таблиц и рисунков в опорном конспекте является автономной.

18

Раздел 1. Парная линейная регрессия

Вразделе рассматриваются три темы:

1.Классическая линейная модель парной регрессии.

2.Оценка качества модели парной регрессии.

3.Прогноз по модели парной регрессии.

По каждой теме излагается основной теоретический материал и приводятся иллюстрирующие его примеры.

После проработки теоретического материала раздела студентам очнозаочной и заочной форм обучения надо выполнить задания контрольной работы в соответствии со своим вариантом. Студенты очной формы обучения во время первой практической работы выполняют задания, приведенные в контрольной работе.

После изучения данного раздела необходимо ответить на вопросы теста № 1. Более подробная информация по данной теме содержится в учебнике [1].

1.1.Классическая линейная модель парной регрессии

Изучаемые вопросы:

взаимосвязи экономических переменных;

педпосылки модели;

оценка параметров парной регрессии методом наименьших квадратов;

статистические свойства МНК-оценок.

При работе с теоретическим материалом следует разобрать примеры решения задач и ответить на контрольные вопросы, приведенные в конце темы.

Взаимосвязи экономических переменных

Одной из основных задач в экономических исследованиях является анализ взаимосвязей экономических показателей. Обычно согласно некоторой экономической гипотезе выделяют зависимые и независимые переменные. Зависимую переменную называют также результативным признаком,

19

объясняемой или эндогенной переменной, независимую переменную – факторной, объясняющей или экзогенной переменной.

Зависимость между переменными может быть строгой (функциональной) либо статистической. Связь между показателями называется функциональной, если каждому значению x соответствует определенное значение y , т. е. y =ϕ(x), где ϕ – обычная числовая функция.

В экономике функциональная зависимость между переменными проявляется редко. Обычно на связь переменных накладывается воздействие случайных факторов и каждому конкретному значению объясняющей переменной соответствует не одно, а множество значений зависимой переменной, точнее, некоторое вероятностное распределение зависимой переменной.

Если при изменении значений x изменяется закон распределения случайной величины y , то зависимость переменной y от переменной x

называется статистической. Для изучения статистической зависимости необходимо располагать большими совокупностями наблюдений переменной y для каждого значения переменной x . Обычно исследуют, как изменяется среднее значение y при изменении значений x . Зависимость, при которой

изменение x приводит к изменению математического ожидания случайной величины y , называется корреляционной.

Функцией регрессии (уравнением регрессии) y на x называется функция,

описывающая изменение условного математического ожидания (среднего значения) зависимой переменной y при изменении x :

корреляционная зависимость отсутствует.

Реальное значение зависимой переменной y не всегда совпадает с ее

20

статистическую суть зависимости, вводят случайную составляющую u , которая является случайной величиной. Таким образом, связь между зависимой

которая называется регрессионной моделью.

В зависимости от количества факторов регрессионные модели подразделяются на модели парной регрессии и модели множественной регрессии. В парной регрессионной модели результативная переменная зависит только от одной факторной переменной.

Отметим характерную особенность эконометрической модели – наличие двух составляющих: неслучайная составляющая f (x) – это часть зависимой переменной, которая полностью объясняется значением независимой переменной x , случайная составляющая u – часть зависимой переменной, которая не может быть объяснена значением x .

Построение регрессионной модели выполняется в несколько этапов:

•спецификация модели;

•сбор статистической информации;

•оценка параметров модели (параметризация);

•проверка адекватности модели (верификация). Остановимся чуть подробнее на каждом из этапов.

На этапе спецификации модели определяется набор экономических

переменных, описывающих функционирование системы, и устанавливается их взаимосвязь. Основная задача, решаемая на этом этапе, – выбор вида функции регрессии в эконометрической модели. В зависимости от типа уравнения регрессии регрессионные модели подразделяются на линейные и нелинейные.

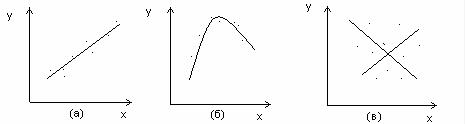
В случае парной регрессии формулу связи выбирают по графическому представлению данных наблюдений в виде точек в декартовой системе координат. Такой график называется корреляционным полем (диаграммой рассеяния). На рис. 1.1.1 изображены три ситуации. На графике (а) взаимосвязь

21

x и y близка к линии. На графике (б) связь, скорее всего, описывается нелинейной функцией, а на графике (в) взаимосвязь между x и y отсутствует.

Рис. 1.1.1

Основой эконометрических моделей являются статистические данные, сбор которых осуществляется на втором этапе. В эконометрике рассматривается два типа выборочных данных.

Пространственными являются данные по некоторому экономическому показателю, полученные для разных объектов за один и тот же период или момент времени. Например, данные о количестве работников, доходе разных фирм в один и тот же момент времени.

Временные данные (временные ряды) – это данные, характеризующие один и тот же объект в различные моменты времени. Например, месячные или ежеквартальные данные о средней заработной плате, инфляции, ежедневный курс доллара. Отличительной особенностью временных данных является упорядоченность этих данных по времени. Кроме того, наблюдения в близкие моменты времени часто бывают зависимы.

На третьем этапе определяются параметры модели. При этом следует иметь в виду, что на практике множество возможных реализаций экономических показателей (генеральная совокупность) неизвестно. Исследователь располагает выборочными значениями показателей (выборочная совокупность), с помощью которых можно оценить, а не определить точно значения параметров модели. Эти оценки являются случайными. Цель оценивания – получить как можно более точные значения неизвестных параметров генеральной совокупности.

22

На четвертом этапе проверяется соответствие модели эмпирическим данным. Если модель неадекватна, то снова выполняются этапы построения модели и параметризации.

Если эконометрическая модель удовлетворяет всем требованиям качества, то она может быть использована для задач анализа и прогнозирования исследуемых экономических процессов. Процесс построения, изучения и применения эконометрических моделей называется эконометрическим моделированием.

Предпосылки модели

Парная линейная регрессионная модель имеет вид

где y – зависимая переменная – результативный признак (случайная величина); x – факторная переменная (детерминированная величина); a0, a1 – параметры модели (постоянные неизвестные коэффициенты); u – случайное возмущение или отклонение (случайная величина), характеризующее отклонение от уравнения регрессии f (x)=a0 +a1x (теоретической линейной зависимости).

Наличие случайного члена u (ошибки регрессии) связано с воздействием на зависимую переменную других неучтенных в уравнении факторов, с возможной нелинейностью модели и ошибками измерения.

Уравнения для отдельных наблюдений зависимой переменной y

записываются в виде

Зависимость дисперсии возмущения от номера наблюдения называется

гетероскедастичностью.

3. Возмущения для разных наблюдений являются некоррелированными:

т. е. предполагается отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях i и j. В случае нарушения данного условия говорят об автокорреляции возмущений.

4.x – детерминированная (неслучайная) величина.

5.Возмущения являются нормально распределенными случайными

Регрессионная модель с учетом условий Гаусса-Маркова (1.1.5)-(1.1.7)

называется классической регрессионной моделью. Если в предпосылки регрессионной модели включено условие нормального распределения возмущения, то модель называется классической нормальной регрессионной моделью.

Для получения уравнения регрессии достаточно первых четырех предпосылок. Требование выполнения пятой предпосылки необходимо для оценки точности уравнения регрессии и его параметров.

Точные значения параметров модели могут быть определены с использованием значений переменных x и y всей генеральной совокупности,

что практически невозможно. Поэтому задача линейного регрессионного анализа состоит в том, чтобы по имеющимся статистическим данным (xi , yi ), i =1, K, n , для переменных x и y получить наилучшие оценки неизвестных

24

параметров. Следовательно, по выборке нужно построить так называемое

неизвестных параметров a0 и a1, называемые коэффициентами регрессии.

Для оценки параметров a0 и a1 обычно применяют метод наименьших квадратов (МНК). Существуют и другие методы оценки параметров, например метод моментов, метод максимального правдоподобия.

Оценка параметров парной регрессии методом наименьших квадратов

Пусть по выборке (xi , yi ), i =1, K, n , требуется определить оценки b0, b1,

т. е. построить выборочное уравнение регрессии (1.1.9) yˆ =b0 + b1x .

Очевидно, наблюдаемые значения yi не будут совпадать с расчетными значениями, вычисленными по формуле (1.1.9): yˆi =b0 + b1xi . Обозначим через ei разность

(1.1.10)

Случайная величина ei называется остатком регрессии в i-м наблюдении.

Методом наименьших квадратов называется метод нахождения неизвестных параметров функции регрессии из условия, чтобы сумма квадратов остатков была минимальной:

25

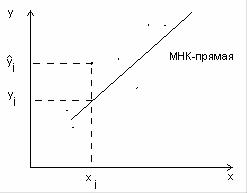
С геометрической точки зрения минимизация суммы квадратов отклонений (1.1.11) означает выбор прямой, которая ближе всего “прилегает” по ординатам к системе выборочных точек (xj,yj), что показано на рис. 1.1.2.

Рис. 1.1.2.

Нетрудно заметить, что функция Q является квадратичной функцией двух параметров b0 и b1, поскольку xi , yi , i =1, K, n – известные данные наблюдений.

Так как функция Q непрерывна, выпукла и ограничена снизу (Q ≥ 0 ), то она имеет минимум. Необходимым условием существования минимума функции двух переменных является равенство нулю ее частных производных по неизвестным параметрам b0 и b1:

После преобразований получим следующую систему нормальных уравнений:

Разделив оба уравнения системы (1.1.12) на n , получим:

выборочные средние.

27

Пример 1.1.1

В табл. 1.1.1 приведены данные о зависимости объема продаж y (тыс. шт.)

от расходов на рекламу x (усл. ед.) по 8 предприятиям концерна.

Таблица 1.1.1

Решение. Коэффициенты регрессии b1, b0 вычислим по формулам (1.1.17).

Для удобства вычисления сумм оформим в виде табл. 1.1.2.

Таблица 1.1.2

В результате получим

b0 = y − b1 x =16,9 − 2,78 3,85 = 6,18.

Таким образом, уравнение парной линейной регрессии имеет вид yˆ = 6,18 + 2,78x .

28

Полученные значения коэффициентов легко проверить с помощью стандартных статистических функций MS Excel НАКЛОН(Y;X) и ОТРЕЗОК(Y;X) соответственно.

Величина b1 показывает, что с увеличением расходов на рекламу на 1 усл.

ед. объем продаж предприятия возрастает в среднем на 2,78 тыс. шт. Величина b0 имеет значение объема продаж предприятия в случае отсутствия рекламы.

Статистические свойства МНК-оценок

Рассмотрим вопросы качества и точности полученных оценок. Найденные по МНК коэффициенты являются лишь выборочными

точечными оценками истинных параметров регрессии. Выборочные оценки b0

и b1 являются случайными величинами, так как зависят от выборки xi и yi , а

также от метода расчета. Критериями качества точечных оценок в статистике являются такие их свойства, как несмещенность, состоятельность и эффективность.

Учитывая, что y = a0 + a1x + u , и воспользовавшись разложением

cov(x, y)= cov(x,a0 + a1x + u)= a1 cov(x, x)+ cov(x,u)= a1Sx2 + cov(x,u),

выражения (1.1.14) для b0 и b1 можно представить в эквивалентном виде

Таким образом, выборочные коэффициенты регрессии представлены в виде суммы постоянной составляющей (истинного значения) и случайной составляющей, зависящей от случайного отклонения модели u , а значит, и от свойств u .

Из (1.1.19) находятся статистические характеристики коэффициентов b0 и

b1.

Из выражений (1.1.20)-(1.1.22) следует, что оценки параметров b0 и b1

являются несмещенными (математическое ожидание оценки равно истинному значению) и состоятельными. Действительно, оценка состоятельна, если сходится по вероятности к истинному значению параметра. Для несмещенных оценок достаточным условием сходимости является сходимость их дисперсии к нулю при неограниченном возрастании объема выборки. Справедлива также теорема Гаусса-Маркова.

Теорема Гаусса-Маркова. Если регрессионная модель (1.1.3) удовлетворяет условиям (1.1.5)-(1.1.8), то МНК-оценки имеют наименьшую дисперсию в классе всех линейных несмещенных оценок (являются эффективными оценками).

Несмещенной оценкой дисперсии возмущений σ2 является величина

которая служит мерой разброса зависимой переменной и называется

остаточной дисперсией. Величина S называется стандартной ошибкой регрессии.

Несмещенные оценки дисперсий коэффициентов b0 и b1 получаются путем

30

Величины Sb1 и Sb0 – стандартные отклонения (ошибки) МНК-

коэффициентов регрессии.

После этапа оценивания модели следует этап проверки ее качества, который включает:

•проверку статистической значимости оценок параметров регрессии;

•построение доверительных интервалов параметров регрессии, дающих определенные гарантии точности их оценок;

•проверку общего качества уравнения регрессии;

•проверку качества прогнозов результативного признака.

Пример 1.1.2

Для данных примера 1.1.1 рассчитать стандартную ошибку регрессии и стандартные ошибки коэффициентов регрессии.

Решение. Подставляя рассчитанные в примере 1.1.1 значения b0 и b1 в

формулу yˆi = b0 + b1 xi , найдем значения yˆi и разместим их в седьмом столбце табл. 1.1.3.

Таблица 1.1.3

31

В восьмом столбце таблицы рассчитаем значения (yi − yˆi )2 . Вычислив

соответствующие суммы, найдем несмещенную оценку дисперсии ошибки σ2 по формуле (1.1.23) и оценки дисперсий коэффициентов регрессии по формулам (1.1.24):

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1.Какая зависимость называется статистической?

2.Какая связь между переменными называется корреляционной?

3.Какая функция называется функцией регрессии?

4.Чем отличаются парная и множественная регрессионные модели?

5.Перечислите этапы построения модели регрессии.

6.Как выглядит линейная модель парной регрессии?

7.Каковы предпосылки классической регрессионной модели?

8.Назовите основные причины наличия в регрессионной модели случайного отклонения.

9.В чем суть метода наименьших квадратов (МНК) и для чего он используется?

10.Приведите формулы расчета оценок коэффициентов линейной модели по МНК.

11.Дайте содержательную интерпретацию коэффициента регрессии в линейном парном уравнении регрессии?

12.Какими свойствами обладают МНК-оценки классической линейной эконометрической модели?

13.Как оценивается дисперсия истинной ошибки модели?

32

1.2. Оценка качества модели парной регрессии

Изучаемые вопросы:

показатели качества регрессии;

проверка значимости коэффициентов парной регрессии.

При работе с теоретическим материалом следует разобрать примеры решения задач и ответить на контрольные вопросы, приведенные в конце темы.

Показатели качества регрессии

Качество уравнения регрессии оценивается по тому, как хорошо уравнение регрессии согласуется со статистическими данными. Другими словами, насколько широко рассеяны точки наблюдений относительно линии регрессии.

Пусть на основе выборочных наблюдений (xi , yi ), i =1, n построено уравнение регрессии, тогда значение зависимой переменной y в каждом наблюдении можно разложить на две составляющие: yi = yˆi +ei . В качестве меры общего разброса значений зависимой переменной y вокруг среднего значения y возьмем сумму квадратов отклонений (вариацию) y от y . Общая вариация может быть разложена на две составляющие:

Часто уравнение (1.2.1) записывают в следующих обозначениях:

TSS=ESS+RSS,

i

sum of squares);

33

Величина R2 показывает, какая доля вариации зависимой переменной обусловлена вариацией объясняющей переменной.

Из формулы (1.2.2) следует, что в общем случае справедливо соотношение

0 ≤ R2 ≤1. При R2 = 0 вариация зависимой переменной полностью обусловлена

Таким образом, чем ближе значение коэффициента детерминации к 1, тем лучше качество подгонки регрессионной модели к наблюденным значениям yi .

Заметим, что вычисление R2 корректно лишь в том случае, когда константа b0 включена в уравнение регрессии. Только в этом случае справедливо разложение (1.2.1).

Для определения статистической значимости коэффициента детерминации

34

F = 0 в том случае, если R 2 = 0 . Поэтому, проверяя значимость F- статистики, мы можем проверить статистическую значимость коэффициента детерминации.

35

Еще одним показателем качества модели регрессии является средняя ошибка аппроксимации:

Чем меньше рассеяние эмпирических точек вокруг теоретической линии регрессии, тем меньше средняя ошибка аппроксимации. Ошибка аппроксимации меньше 7 % свидетельствует о хорошем качестве модели.

Пример 1.2.1

Для данных примера 1.1.1 рассчитать выборочный коэффициент корреляции.

Решение. Выборочный коэффициент корреляции вычислим по формуле

Полученное значение можно проверить с помощью стандартной

статистической функции КОРРЕЛ(X;Y).

Пример 1.2.2

Вычислить коэффициент детерминации R2 и F-статистику для регрессии, оцененной в примере 1.1.1.

Решение. По формуле (1.2.2) рассчитаем величину выборочного коэффициента детерминации. Значения ESS и TSS вычислены в табл. 1.1.3 и

расположены в строке “сумма” восьмого и девятого столбцов.

функции Fраспобр. Параметры функции: вероятность – уровень значимости

α , число степеней свободы 1 – для парной регрессии 1, число степеней свободы 2 – для парной регрессии 2.

Проверка значимости коэффициентов парной регрессии

При проверке качества модели наиболее важной является задача установления наличия линейной зависимости между результативной и факторной переменными.

Мы выбрали регрессионную модель в виде (1.1.3). В действительности может оказаться, что фактор x не влияет на результативный признак, и потому параметр a1 должен быть равен нулю. Значение оценки b1, найденное для конкретной выборки, при этом может быть отличным от нуля. Для проверки существенности отклонения b1 от нуля проверяется значимость коэффициента.

исходных предпосылок модели эта величина имеет распределение Стьюдента с числом степеней свободы ν = n −2 , где n – число наблюдений.

Если модуль вычисленного по выборке (фактического) значения

38

Если в границы доверительного интервала попадает ноль, то оцениваемый коэффициент принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.

Пример 1.2.3

Выполнить проверку значимости коэффициента b1, оцененного в примере

1.1.1, для уровня значимости α =5 % .

Решение. Оцененную регрессионную модель обычно записывают следующим образом:

yi =b0 + b1 xi + ui

(Sb0 ) (Sb1 ) (S),

1.Приведите формулу расчета коэффициента детерминации R2 . Что характеризует коэффициент детерминации? В каких пределах изменяется коэффициент детерминации для парной линейной регрессии?

2.Как связаны коэффициент корреляции и коэффициент детерминации для парной линейной регрессии?

3.Приведите формулу расчета выборочного коэффициента корреляции. Назовите основные свойства выборочного коэффициента корреляции.

39

4.Как связан коэффициент линейной регрессии с выборочным коэффициентом корреляции?

5.С помощью какого критерия проверяется значимость коэффициентов регрессии? Каков алгоритм проверки значимости коэффициентов регрессии?

1.3. Прогноз по модели парной регрессии

Изучаемые вопросы:

предсказание среднего значения;

предсказание индивидуального значения зависимой переменной;

использование MS Excel при решении задач регрессионного анализа. После изучения темы Вам следует ответить на вопросы для самопроверки.

Под прогнозированием в эконометрике понимается построение оценки зависимой переменной для значений независимой переменной, которых нет в исходных наблюдениях. Рассматривают два вида прогнозов для определенного значения факторной переменной: предсказание условного математического ожидания зависимой переменной (ожидаемого или среднего значения) и предсказание индивидуального значения зависимой переменной.

Предсказание среднего значения

Пусть построено уравнение парной регрессии yˆi = b0 +b1 xi . На основе построенной модели рассчитываются точечные и интервальные прогнозы. Точечный прогноз при x = x0 получается путем подстановки значения x = x0 в

уравнение регрессии:

(1.3.1) yˆ0 является точечной оценкой условного математического ожидания

(среднего значения) переменной y при x = x0 . Чтобы измерить точность полученной оценки и построить доверительный интервал для среднего