Точечные оценки математического ожидания и дисперсии

Пусть случайная выборка порождена наблюдаемой случайной величиной ξ, математическое ожиданиеи дисперсиякоторой неизвестны. В качестве оценок для этих характеристик было предложено использовать выборочное среднее

и выборочную дисперсию

. (3.14)

Рассмотрим некоторые свойства оценок математического ожидания и дисперсии.

1. Вычислим математическое ожидание выборочного среднего:

. (3.15)

Следовательно, выборочное среднее является несмещенной оценкой для .

2. Напомним, что результаты наблюдений – независимые случайные величины, каждая из которых имеет такой же закон распределения, как и величина, а значит,,,. Будем предполагать, что дисперсияконечна. Тогда, согласно теореме Чебышева о законе больших чисел, для любогоε> 0 имеет место равенство,

которое можно записать так: . (3.16)

Сравнивая (3.16) с определением свойства состоятельности (3.11), видим, что оценка является состоятельной оценкой математического ожидания.

3. Найдем дисперсию выборочного среднего:

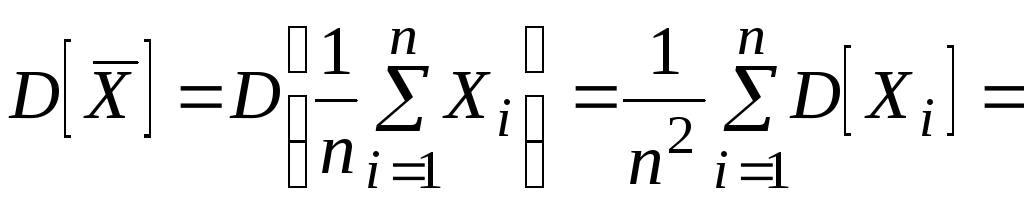
. (3.17)

Таким образом, дисперсия оценки математического ожидания уменьшается обратно пропорционально объему выборки.

Можно доказать, что если случайная величина ξраспределена нормально, то выборочное среднееявляется эффективной оценкой математического ожидания, то есть дисперсияпринимает наименьшее значение по сравнению с любой другой оценкой математического ожидания. Для других законов распределенияξэто может быть и не так.

Выборочная дисперсия является смещенной оценкой дисперсии, так как. (3.18)

Действительно, используя свойства математического ожидания и формулу (3.17), найдем

.

Чтобы получить несмещенную оценку дисперсии, оценку (3.14) нужно исправить, то есть домножить на . Тогда получим несмещенную выборочную дисперсию

. (3.19)

Отметим, что формулы (3.14) и (3.19) отличаются лишь знаменателем, и при больших значениях выборочная и несмещенная дисперсии отличаются мало. Однако при малом объеме выборкиследует пользоваться соотношением (3.19).

Для оценки среднего квадратического отклонения случайной величины используют так называемое “исправленное” среднее квадратическое отклонение, которое равно квадратному корню из несмещенной дисперсии: .

3.4. Интервальные оценки

В статистике имеются два подхода к оцениванию неизвестных параметров распределений: точечный и интервальный. В соответствии с точечным оцениванием, которое рассмотрено в предыдущем разделе, указывается лишь точка, около которой находится оцениваемый параметр. Желательно, однако, знать, как далеко может отстоять в действительности этот параметр от возможных реализаций оценок в разных сериях наблюдений.

Ответ на этот вопрос – тоже приближенный – дает другой способ оценивания параметров – интервальный. В соответствии с этим способом оценивания находят интервал, который с вероятностью, близкой к единице, накрывает неизвестное числовое значение параметра.