Гистограмма

Если наблюдаемая случайная величина ξнепрерывна или объем выборкибольшой, то вариационный и статистический ряды будут трудно обозримыми множествами, практически не будет равных элементов выборки. В этом случае используется процедура группировки выборки, которую рассмотрим для реализации выборки. Интервал возможных значенийξделят точкаминанепересекающихся полуинтервалов (разрядов),. Для каждого разрядаподсчитывают частоту- число элементов выборки, попавших в этот разряд. При этом. В интервал включают значения, большие или равные нижней границе и меньше верхней границы. Далее находят относительные частоты (статистические вероятности). Группированные данные удобно представить в виде интервального статистического ряда – последовательности пар, или в виде таблицы (табл. 3.3). Часто группу элементов выборки, входящих в интервал, заменяют средней точкой.Таблица 3.3

			…
			…

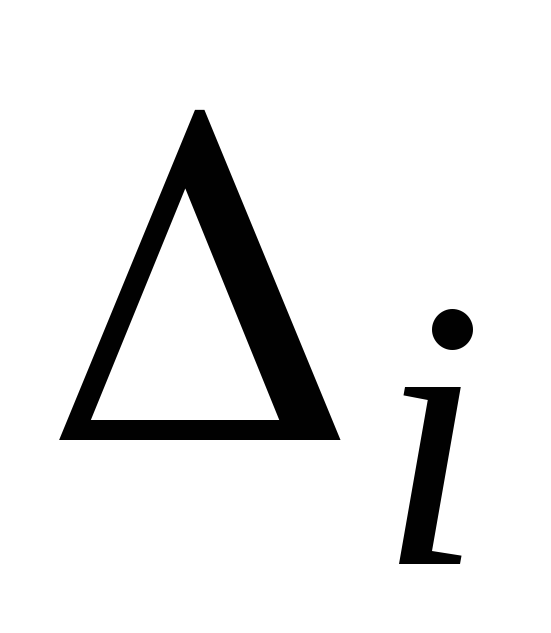
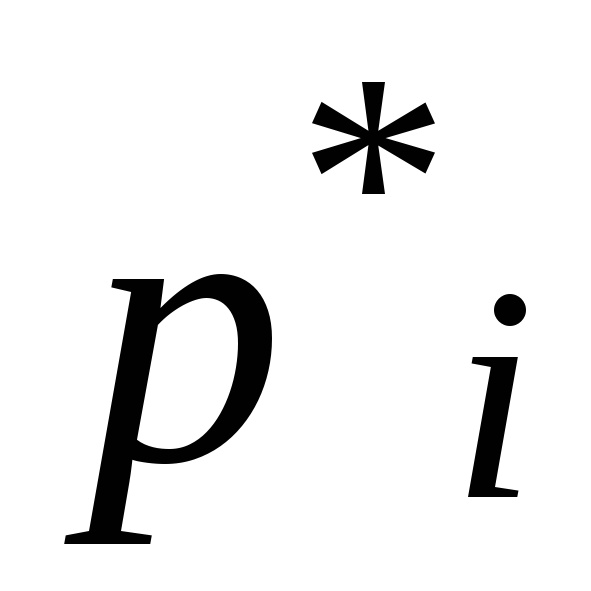
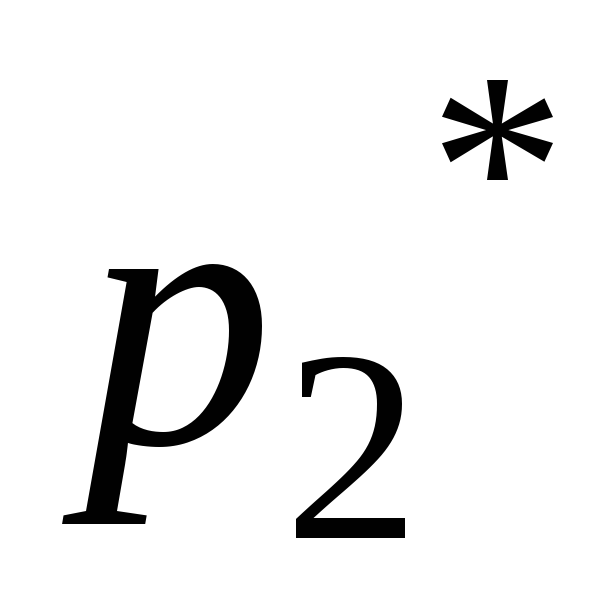
Обычно длина разрядов выбирается одинаковой, т.е. равной . Число разрядоввыбирается в зависимости от объема выборкитак, чтобы построенный ряд не был громоздким и в то же время позволял выявить характерные особенности изменения случайной величины. Для определенияможно рекомендовать формулу Стерджеса

, (3.4)

которая дает нижнюю оценку величины . В качестве значенияследует брать ближайшее целое число.

Группированный статистический ряд наглядно можно изобразить в виде гистограммы. Для ее построения на оси абсцисс откладывают разряды длиною, и на каждом из них, как на основании, строят прямоугольник. В результате получают ступенчатую фигуру, которую называютгистограммой.

Высота i–го частичного прямоугольника при построении гистограммы частот равна отношению (плотность частоты).

Площадь i–го частичного прямоугольника численно равна ,

а площадь гистограммы частот численно равна объему выборки, т.е.

.(3.5)

При построении гистограммы относительных частот:

высота i–го частичного прямоугольника равна отношению относительной частоты к длине интервала (плотность относительной частоты); площадьi–го частичного прямоугольника численно равна ; площадь гистограммы относительных частот численно равна

1. (3.6)

Гистограмма относительных частот является статистическим аналогом плотности распределения наблюдаемой случайной величины ξ.

Гистограмма изображена на рис. 3.4.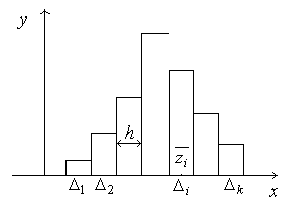

Рис. 3.4

3.3. Точечные оценки параметров распределения

На практике часто удается предсказать или оценить с помощью гистограммы вид распределения наблюдаемой случайной величины ξс точностью до неизвестного параметра(или нескольких параметров). Одной из основных задач математической статистики является нахождение оценки (приближенного значения) неизвестного параметра по имеющейся выборке.

Основные понятия

Пусть наблюдается случайная величина ξс функцией распределенияи плотностью распределения. Случайная выборка представлена векторомс реализацией. (3.7)

Параметром распределенияслучайной величиныназывается любая числовая характеристика этой случайной величины (математическое ожидание, дисперсия и т.п.) или любая константа, явно входящая в выражение для функции или плотности распределения.

Если параметр неизвестен, то его точечной оценкойназывается произвольная функция элементов выборки

. (3.8) Реализацию оценки, т.е. значение оценки для наблюдавшейся в эксперименте реализации выборки, принимают за приближенное значение неизвестного параметра

Из соотношения (3.8) видно, что как функция случайных величин сама также является случайной величиной. Закон распределения оценкизависит от вида функции, числа наблюдений и значения оцениваемого параметра.

Ясно, что существует много разных способов построения точечной оценки, и не всякая зависимость может давать удовлетворительную оценку неизвестного параметра. Рассмотрим некоторые свойства, которыми должна обладать оценка, чтобы ее можно было считать хорошим приближением к неизвестному параметру.

Оценка параметраназываетсянесмещенной, если ее математическое ожидание равно оцениваемому параметру, то есть

. (3.9)

Если свойство (2.2) не выполняется, то есть

, (3.10)

то оценку называютсмещенной, при этом величинуназывают систематической ошибкой оценки.

Требование несмещенности означает, что выборочные значения оценок, полученных в результате повторения выборок, группируются около оцениваемого параметра.

Оценка параметраназывается состоятельной, если приона сходится по вероятности к оцениваемому параметру, т.е. для любогоε> 0 выполняется равенство

. (3.11)

Следующая теорема устанавливает достаточные условия состоятельности оценки параметра.

Теорема. Если прии, то оценкапараметраявляется состоятельной.

Состоятельность оценки означает, что, при достаточно большом объеме выборки с вероятностью близкой к единице, отклонение оценки от истинного значения параметра меньше ранее заданной величины.

Обычно в качестве меры точностиоценкииспользуется среднеквадратическая ошибка (среднее значение квадрата ошибки). Очевидно, чем меньше эта ошибка, тем теснее сгруппированы значения оценки около оцениваемого параметра. Поэтому всегда желательно, чтобы ошибка оценки была по возможности малой. Используя свойства математического ожидания, нетрудно получить

. (3.12)

Для несмещенных оценок

, (3.13)

то есть их мерой точности является дисперсия.

Несмещенная оценка параметра называется егоэффективной оценкой, если ее дисперсияявляется наименьшей среди дисперсий всех возможных оценок параметра, вычисленных по одному и тому же объему выборки.