1.3.4. Формула полной вероятности и формула Байеса

Теорема. Пусть A - некоторое событие, и события H₁, H_2, , H_n , _, попарно несовместные, т.е. H_i H_j= , ij, образующие полную группу, и появление одного из них и только одного есть событие достоверное.

Допустим, что событие A может произойти вместе с одним из событий H_i Тогда имеет место формула полной вероятности

p(A) = p( A  H_i) (1.10)

и формула Байеса p(H_i  A)=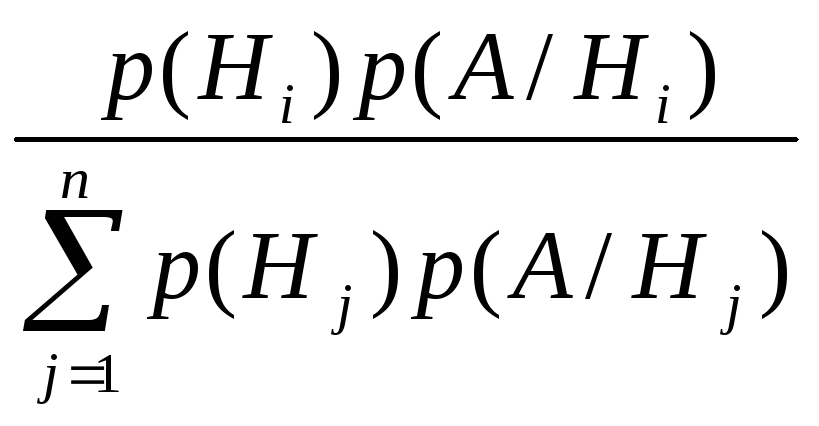. (1.11)

Замечание. События H_i называют гипотезами, вероятности p(H_i) - априорными вероятностями гипотез H_i, а вероятности p(H_iA) - апостериорными вероятностями гипотез H_i.

Пример 1.19. В первой урне находится 4 белых и 6 черных шаров, а во второй – 2 белых и 7 черных шаров. Из первой урны во вторую наудачу перекладывают один шар. После этого из второй урны наудачу извлекают один шар.

1) Найти вероятность, что шар, извлеченный из второй урны, белый.

2) Известно, что из второй урны извлечен белый шар. Найти вероятность того, что из первой урны во вторую был переложен черный шар.

Решение. Обозначим события

H₁ = {из первой урны во вторую был переложен белый шар},

H₂ = {из первой урны во вторую был переложен черный шар},

A = {шар, извлеченный из второй урны, белый}.

а) По классическому определению вероятности находим вероятности гипотез H₁ и H₂ :

p(H₁) - вероятность того, что из всех находящихся в первой урне шаров во вторую был переложен белый шар - p(H₁) = 4 / 10 = 0,4,

p(H ₂) - - вероятность того, что из всех находящихся в первой урне шаров во вторую был переложен черный шар - p(H₂) = 6/ 10 = 0,6,

и условные вероятности:

p(A/H₁) – вероятность того, что из второй урны будет вынут белый шар, при условии, что в нее был переложен белый шар - p(A/H₁) = 3/10 = 0,3.

p(A/H₂) - вероятность того, что из второй урны будет вынут белый шар, при условии, что в нее был переложен черный шар - p(A/H₂) = 2/10 = 0,2.

Тогда по формуле полной вероятности находим вероятность искомого события A

p(A) = p(H₁) p(A/H₁)+p(A/H₂)p(H₂) = 0,40,3 +0,60,2 = 0,24.

б) Во второй части задачи требуется найти условную вероятность p(H₂/A). Для этого можно использовать формулу Байеса (1.11):

p(H₂/A) = .

Вопросы для самопроверки

1. Какие условия должны быть выполнены для проведения опытов по схеме Бернулли?

2. По какой формуле вычисляется условная вероятность?

3. Как вычисляется вероятность произведения:

а) для независимых событий?

б) для несовместных событий?

в) для любых других типов событий?

4. В чем смысл формулы полной вероятности?

В результате изучения материала раздела 1 студент может выполнить задание № 1 из методических указаний по выполнению контрольной работы по вычислительной математике, основам теории вероятностей и элементам математической статистики [ 8 ] .

Раздел 2. Случайные величины

В этом разделе содержится материал о случайных величинах: дискретных и непрерывных. Приводятся определения и описываются способы задания случайных величин с помощью ряда распределения и функции распределения. Способы определения плотности вероятности зависят от того, какое распределение имеет случайная величина. Рассматривается решение задач, в которых необходимо вычислить числовые характеристики случайных величин, а также написать выражение для плотности вероятности случайной величины, если она имеет биномиальное распределение, равномерное распределение или нормальное распределение.

Изучение материала раздела заканчивается ответами на вопросы для самопроверки и рассмотрением репетиционного теста №2, приведенного в блоке контроля и освоения дисциплины. После того, как эта часть работы проделана, студент может приступить к выполнению задачи № 2 из методических указаний к выполнению контрольной работы по вычислительной математике, основам теории вероятностей и элементам математической статистики [ 8 ].