4.Функция выбора

Функция выбора, одно из наиболее абстрактных понятий теории принятия решений. Сам выбор часто ставит перед человеком проблемы неопределенности. Достаточно вспомнить сообщение: «Казнить нельзя помиловать». Положение запятой в этом выражении кардинальным образом меняет смысл сообщения. Такие же проблемы вынужден решать менеджер при принятии решений по управлению фирмой. При этом он вынужден не только прогнозировать будущее состояние фирмы и экономической внешней среды, в которой она будет действовать, но и пожелания собственника, которые также не всегда осуществимы.

Функция выбора ставит в соответствие каждому рассматриваемому множеству объектов (альтернатив, вариантов) некоторое его подмножество, трактуемое как множество выбираемых объектов. Пусть - множество всех потенциальных объектов выбора,- некоторое семейство его непустых подмножеств. Тогда функцией выбора наназывается отображение, такое, чтопри всех. Нередко на функцию выбора налагают дополнительные требования – в частности, непустота выбора:при всех, или, более того, одиночность выбора:(одноэлементное множество).

Иногда функцией выбора называются функции несколько более общего вида, допускающие зависимость от параметров. В частности, функция выбора может рассматриваться как параметрически зависящая от той структуры данных , на основе которой совершается выбор:. Например, в ролиможет выступать отношение предпочтения лица, принимающего решение, или набор предпочтений всех членов коллектива. Еще одна возможность параметризации функции выбора – зависимостьот параметра:. В результате функция выбора преобразуется в функцию. Последнее представление встречается в теории потребительского спроса.

Первоначальная интерпретация множеств иподразумевала, что всякое- это совокупность взаимоисключающих объектов выбора. Поэтому в реальном акте выбора реализуется какая-либо одна альтернатива. Множествотрактовалось как совокупность всех тех и только тех альтернативиз, каждая из которых является предпочтительной в том или ином смысле. В последующем развитии теории выбора интерпретацииистали более широкими. Так, если в роливыступает множество всех потенциально мыслимых состояний системы, то в качествеможно принять множество реализуемых состояний в силу устройства системы. Например,может быть множеством состояний равновесия – экономической системы, абстрактной игры и т.д. В общем случае- это множество чем-либо примечательных, выделенных объектов из, не обязательно «лучших» в обычном понимании. Наконец, само множествоне обязано состоять из взаимоисключающих объектов, и все элементы множествамогут сосуществовать в виде выбранного набора объектов.

Понятие «функция выбора» получило распространение в различных областях, связанных с принятием решений. Термин «функция выбора» введен первоначально в общей теории множеств.

Историческим прототипом абстрактной функции выбора послужила, по-видимому, функция потребительского выбора (спроса), которая в простейшей форме определяется следующим образом. Пусть потребитель может приобретать любые из продуктов в любых количествах по ценам, и пусть он покупает набор продуктов, исходя из оптимизации своей функции полезностипри ограниченном бюджете. Тогда допустимым множеством его выбора является, а выбором – множество всех факторов, максимизирующих функцию полезности:. Для функции однозначного потребительского спросаП. Сэмюэлсоном была введена аксиома выявленного предпочтения (в слабой форме) как необходимое условие того, чтобы поведение потребителя действительно описывалось вышеуказанным образом при какой-либо функции полезности. Эта аксиома послужила отправной точкой для последующих аксиоматических описаний оптимизационного набора. С другой стороны, Г. Черновым была введена система аксиом, характеризующих аналогичную оптимизационную природу выбора статистических решающих правил. В этих работах были заложены основы метода функций выбора на базе характеризующих их свойств, развитых далее К. Эрроу, А. Сеном и другими авторами.

Современную тематику функции выбора можно разделить на три сферы:

1. свойства функции выбора и их взаимосвязи;

2. механизмы порождения функции выбора;

3. применения функции выбора в других областях.

Свойства функции выбора обычно описываются в терминах изменения выбора при определенных изменениях предъявлений. Функции выбора может рассматриваться как внешне «входо-выходное» описание некоторого механизма выбора, ее порождающего, т. е. преобразующего входв выходпо некоторому правилу, действующему на некоторой структуре данных. Важное значение имеет задача восстановления механизма, способного порождать заданную функцию выбора. Классический пример такой задачи – вопрос о порождаемости функцииоптимизацией какой-либо скалярной функции, т. е. о представимости ее в виде(рациональность выбора в узком смысле). Для конечного множества, семейства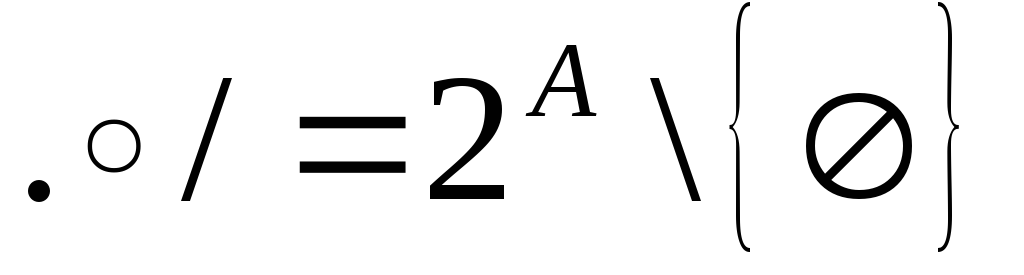и функции непустого выборанаответ дается теоремой Эрроу: необходимо и достаточно выполнение версии слабой аксиомы выявленного предпочтения, в виде,. Аналогично ставится вопрос о рациональности выбора в широком смысле, т. е. о представимостикак множества доминирующих (или недоминируемых) элементов впо некоторому бинарному отношениюна:. Ответ дается обобщенной теоремой Сена: необходимо и достаточно выполнение условия.

С 1980-х годов в экономико-математическом анализе происходит отход от стремления ограничиваться только рациональными в указанном смысле функциями выбора. В ходе исследований выяснилось, что даже достаточно разумно ведущие себя функции выбора могут не порождаться оптимизацией по скалярным критериям или даже бинарным отношениям и вообще не определяться одними лишь парными сравнениями объектов выбора. Для описания таких функций привлекаются более общие структуры – такие, как множественные отношения и гиперотношения (отношения между множествами объектов), параметрические функции и отношения, - и более общие правила выбора на таких структурах.

К «внутренним» задачам теории функции выбора относятся вопросы образования составных функций из нескольких исходных и, обратно, вопросы «разложения» заданных функций выбора на более простые. Такие задачи, как и задачи характеристики механизмов выбора в терминах функции выбора, встречаются, в частности, при изучении методов коллективного принятия решений и игрового взаимодействия участников группы. Функции выбора могут служить средством описания и анализа поведения взаимодействующих индивидов и систем. Основная сфера применения функций выбора – теоретические модели целенаправленного поведения в социальных, экономических и других системах.