В. А. Жилкин

Отсюда вывод48: при решении инженерных задач в пакете MathCAD всегда проверяйте результат с позиций здравого смысла и, если есть возможность, сопоставляйте с результатами приближённых решений рассматриваемой задачи!

8.2. Перемещения при растяжении (сжатии)

Умение вычислять деформации и перемещения необходимо для расчетов на жесткость, а также для определения усилий в статически неопределимых системах.

8.2.1. Перемещение точек оси бруса

Исследуем взаимное перемещение точек C и B оси бруса AD, имеющего площадь поперечного сечения F и нагруженного некоторой системой сил (рис. 8.5).

Рис. 8.5

С осью бруса совместим ось x прямоугольной системы координат xoz, начало которой разместим заделке. Положения точек C и B задаются координатами xB и xC. Произвольное поперечное сечение бруса на участке BC определяется координатой x.

Из соотношений Коши (4.4) относительная продольная деформация в направлении оси x определяется выражением

x u du ,x dx

48 Жилкин В. А. Решение задач земледельческой механики в MathCAD. Челябинск : ЧГАА, 2010. 409 с.

308

ГЛАВА8 Растяжение и сжатие

из которого следует

найдем перемещения точек оси бруса относительно точки B:

мости (8.6) для определения перемещений в произвольном сечении бруса можно придать вид

Из зависимостей (8.7), (8.7*), (8.8), (8.8*) следует, что перемещения произвольного сечения бруса можно вычислять и в системе координат xo (локальной системе координат), размещаемой в начале каждого участка бруса. В этом случае перечисленные формулы примут вид

309

В. А. Жилкин

то удлинение бруса, как это следует из формулы (8.7), равно ( xB 0 и u xB 0 ):

Пример 8.3. Для бруса, изображенного на рис. 8.6 а, построить эпюры N,

x , u.

Всоответствии с общим правилом построения эпюр:

–выбираем систему координат (ось z помещаем в левом крайнем сечении бруса, а ось x направляем вдоль его оси);

–изображаем расчетную схему бруса;

–разбиваем брус вдоль его оси на участки, в пределах которых одновременно должны оставаться постоянными следующие

величины:

1) выражения для внутренних усилий N, если хотят построить только эпюру N;

2) выражения для внутренних усилий N и площади F, если хо-

тят построить эпюру x ;

3) выражения для внутренних усилий N, площади F, модуля Юнга E, если хотят построить эпюру перемещений u.

310

ГЛАВА8 Растяжение и сжатие

А. Определение опорных реакций В рассматриваемой задаче опорные реакции мож-

но было бы и не определять, если рассматривать не левые, а правые отсеченные части бруса (рис. 8.6, б).

а

б

в

г

д

е

ж

з

и

Рис. 8.6

311

В. А. Жилкин

Отсюда

XA P1 P2 P3 20 кН;

ZA 0 ;

MA 0 .

Итак,

XA 20 кН; ZA 0 кН; MA 0 кН.

Б. Определение внутренних усилий в поперечных сечениях бруса Учитывая только характер приложенной к брусу нагрузки, разбиваем его на три участка: 1, 2 и 3 (рис. 8.6, б). В пределах каждого участка мысленно рассекаем брус на две части, отбрасываем правую часть, а для левой записываем уравнение равновесия системы сил, приложенных к отсечен-

ной части бруса (рис. 8.6, в, г, д).

Участок 1 0 x1 1 м.

X 0 : XA N1 0 ; N1 XA 20 кН.

Участок 2 0 x2 3 м.

X 0 : XA P1 N2 0 ;

N2 XA P1 20 60 40 кН.

312

ГЛАВА8 Растяжение и сжатие

Участок 3 0 x2 3 м.

X 0 : XA P1 P2 N3 0 ;

N3 XA P1 P2 20 60 80 40 кН.

По вычисленным значениям Ni ( i 1, 2, 3 ) строим эпюру N (рис. 8.6, е).

Все ординаты эпюры на чертеже изображаются в одном, выбранном вами, масштабе!

В. Определение напряжений и перемещений Брус разбиваем вдоль его оси на пять участков, в преде-

лах которых выражения для напряжений и перемещений постоянны (рис. 8.6, ж). Для построения эпюр x и u будем использовать локальные системы координат xo . Построение эпюры u целесообразно начать от заделки, т. к. в этом сече-

висит от текущей координаты x1 , и для построения ее графика (отрезка прямой линии) достаточно знать две ее ординаты.

313

В. А. Жилкин

Обычно выбирают точки в начале ( x1 0 м) и в конце участка ( x1 1 м) бруса.

Итак, в пределах первого участка

314

ГЛАВА8 Растяжение и сжатие

Функция u3 x2 линейным образом зависит от текущей координаты x3 , и для построения ее графика (отрезка прямой линии) достаточно знать две ее ординаты в начале ( x3 0 м) и в конце участка ( x3 1 м) бруса.

Итак, в пределах третьего участка

315

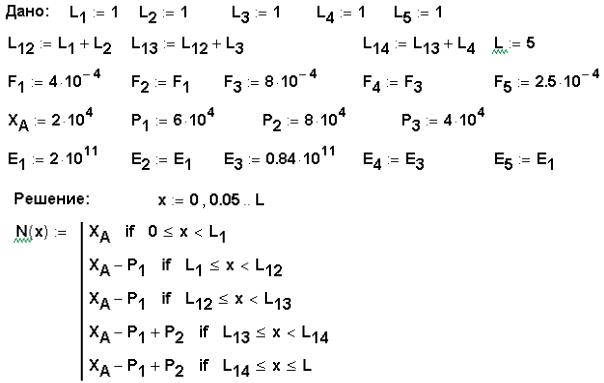
В. А. Жилкин

щей координаты x5 , и для построения ее графика (отрезка прямой линии) достаточно знать две ее ординаты в начале ( x5 0 м) и в конце участка ( x5 1 м) бруса.

Итак, в пределах четвертого участка

x,5 160 МПа; u5 0 uG 0,25 мм;

u5 1 uH 0,55 мм.

По результатам расчета строим эпюры нормальных напряжений x и перемещений поперечных сечений бруса u (рис. 8.6, з и и).

Решим эту же задачу в MathCAD. При записи значений физических и геометрических величин будем использовать систему СИ.

316

ГЛАВА8 Растяжение и сжатие

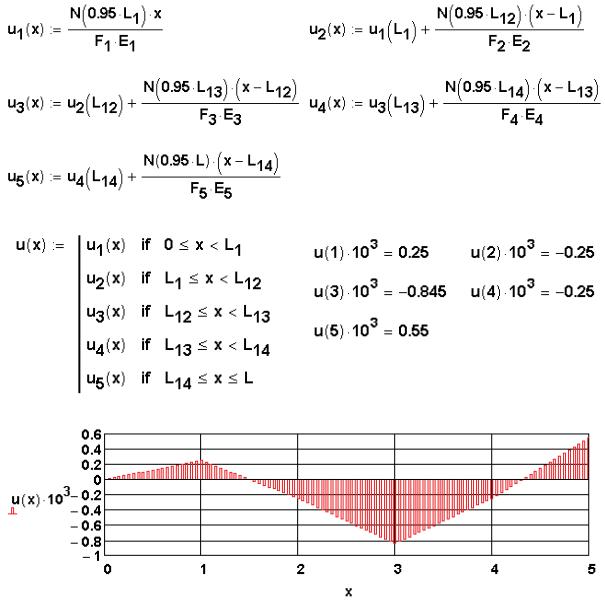
Ввиду громоздкости выражений для перемещений сечений бруса по участкам их целесообразно вычислить отдельно. Для того чтобы не набирать выражения для нормальной силы на каждом из участков используется функция

317

В. А. Жилкин

N x , а так как она в пределах участка постоянна, то можно брать любое значение в пределах участка за исключением крайней правой точки, ибо оно не вычислено ( x Li , i 1, 12, 13, 14 ).

Результаты вычислений в MathCAD полностью совпадают с полученными ранее традиционным путём. Преимущество использования MathCAD состоит в том, что если выражения для вычисляемых величин записаны правильно, то арифметические ошибки отсутствуют.

318

ГЛАВА8 Растяжение и сжатие

Пример 8.4. Определить полное удлинение стального бруса, изображенного на рис. 8.7, а с учётом его собственного веса, если известны объёмный вес материала и его модуль E , а также построить эпюры N , x , u .

Решение. Так как в дальнейшем необходимо будет построить эпюру перемещений поперечных сечений бруса u, то начало координатной системы xoy целесообразно разместить в заделке, т.к. её перемещение равно нулю, а ось x направить вдоль стержня, как показано на рис. 8.7.

Брус имеет два участка, в пределах которых вид нагрузки и геометрические характеристики поперечных сечений не изменяются.

Интенсивности распределённых нагрузок в пределах участков равны произведению удельного веса материала на объём элемента бруса единичной длины: q1 kF 1 kF ;

q2 F 1 F , т.е. q1 kq2 .

Величина опорной реакции RA определяется из условия равновесия системы сил, приложенных к брусу:

319

В. А. Жилкин

X 0 : RA P q1 a q2a 0 .

Откуда

RA P q1 a q2a .

Нормальные силы в пределах участков изменяются по линейному закону и равны

N1 x RA q1 x ; N2 x RA q1 a q2 x a ,

а напряжения –

1 x N1F1 x ; 2 x N2F2x .

Перемещения поперечных сечений бруса в пределах участков (в соответствии с формулой (8.7) будут определяться квадратичными функциями

Все дальнейшие вычисления выполним в MathCAD. Для получения аналитических выражений для полного удлинения бруса сначала используем символьный процессор, а затем для конкретного бруса построим эпюры N , x , u .

320

ГЛАВА8 Растяжение и сжатие

Итак, полное удлинение стального бруса определяется зависимостью

L a k 1 P Fa .

EFk

Если положить k 1 , P 0 , a L2 , то мы получим формулу для определения полного удлинения бруса длиною L , нагруженного только собственным весом.

где G FL – вес стержня, приложенный в центре тяжести стержня, расположенного на расстоянии L2 от заделки, чем и объясняется наличие коэффициента 2 в знаменателе формулы.

Построим эпюры N , x , u для конкретного стержня. Геометрические, физические и силовые параметры стержня приведены в программе.

321