ГЛАВА2 Геометрические характеристики поперечных сечений брусьев

2.7.Свойство моментов инерции относительно осей симметрии

Пусть ось y будет осью симметрии сечения, а ось z ей перпендикулярна (рис. 2.12). В силу симметрии каждой площадке с положительным произведением координат справа будет соответствовать площадка с таким же, но отрицательным произведением координат слева, поэтому

Jyz yzdF 0 .

F

Рис. 2.12

Ось симметрии сечения и любая ось, ей перпендикулярная, есть главные оси сечения.

2.8.Свойство моментов инерции правильных фигур относительно центральных осей

Для правильных фигур (рис. 2.13.) Jyz 0 ; Jy Jz .

Для квадрата последнее равенство очевидно, так как он одинаково расположен относительно осей y и z .

Для остальных фигур это можно доказать следующим образом: в правильной фигуре всегда найдется ось y1 , относительно которой фигура будет расположена так же, как относительно оси y , и потому Jy1 Jy .

101

В. А. Жилкин

Рис. 2.13

В соответствии с зависимостью (2.18)

Jy1 Jy cos2 1 Jz sin2 1

или

Jy 1 cos2 1 Jz sin2 1 ,

откуда Jy Jz . Тогда

Ju Jy cos2 Jz sin2

или Ju Jy .

Моменты инерции правильных фигур относительно центральных осей равны и любые центральные взаимно перпендикулярные оси являются главными.

2.9. Вычисление моментов инерции сложных фигур

Всякую сложную фигуру обычно можно разбить на ряд простых фигур, моменты инерции которых относительно их центральных осей известны.

Способ вычисления моментов инерции сложных сечений основывается на том, что любой интеграл можно рассматривать как сумму интегралов и, следовательно, момент

102

ГЛАВА2 Геометрические характеристики поперечных сечений брусьев

103

В. А. Жилкин

Для определения Jyz поступают следующим образом: из

с помощью формулы (2.27) для случая поворота осей по известным значениям Ju , Jv и величине угла определяется

центробежный момент инерции Jyz Ju Jv sin2 .

2

Алгоритм определения главных моментов инерции сложной фигуры

A.Выбирают некоторую глобальную систему координат так, чтобы сложная фигура была расположена, как правило, в её первой четверти.

B.Разбивают сложную фигуру на ряд простых фигур, определяют координаты центра тяжести простых фигур и проводят через центры тяжести простых фигур центральные оси, параллельные осям глобальной системы координат.

C.Вычисляют площади, статические, осевые и центробежные моменты простых фигур.

D.Определяют координаты центра тяжести сложной фигуры, с которым совмещают начало координат центральных осей всей фигуры, параллельных осям глобальной системы координат.

E.Вычисляют осевые и центробежный моменты инерции заданной фигуры относительно этих осей.

F.Определяют ориентацию главных осей и вычисляют главные моменты инерции фигуры.

2.10.Примеры определения главных центральных осей и главных моментов инерции сечений

Все вычисления будем проводить в системе MathCAD. Пример 2.4. Определить главные моменты и главные радиусы инерции

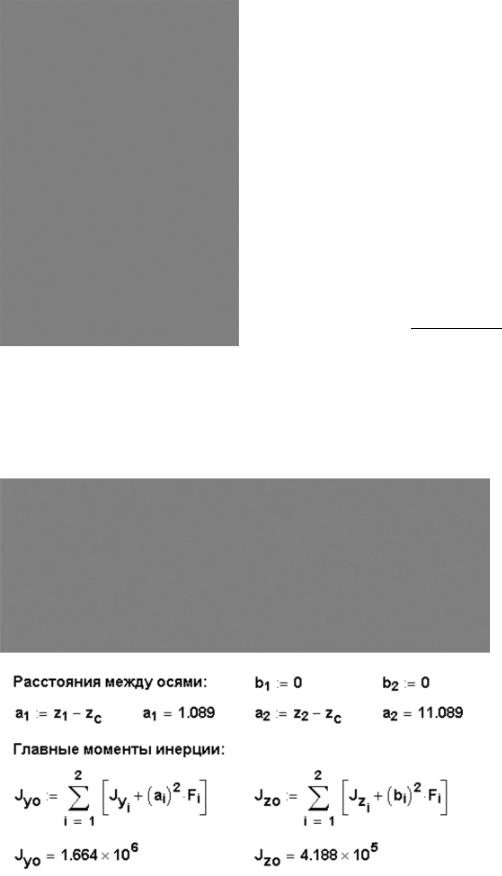
для сечения, представленного на рис. 2.16, m = 20 cм. Решение. Сечение имеет вертикальную ось симметрии и состоит из двух

простых фигур: прямоугольника, с осями симметрии которого

104

ГЛАВА2 Геометрические характеристики поперечных сечений брусьев

совместим глобальную систему координатy1, z1 , и круга радиуса а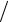2 . Оси y1 , z1 являются главными центральными осями инерции первой фигуры, оси y2 , z2 являются главными центральными осями инерции второй фигуры. Ось симметрии сечения совпадает с главной центральной осью z0 сечения. Вторая главная центральная ось y0 перпендикулярна оси z0 и должна проходить через центр тяжести сечения.

Координату zС центра тяжести сечения найдем, воспользовавшись формулой

zC z1F1 z2F2 , F1 F2

Рис. 2.16

где z1 , z2 – координаты центров тяжести первой и второй фигур;

F1 , F2 – площади простых фигур.

105

В. А. Жилкин

Пример 2.5. Для составного несимметричного сечения из прокатных профилей:

1)найти координаты центра тяжести фигуры;

2)определить положение главных центральных осей инерции;

3)определить величину главных моментов и главных радиусов инерции.

Форма сечения представлена на рис. 2.17. Размеры сечений взять из сортамента прокатной стали.

Рис. 2.17

106

ГЛАВА2 Геометрические характеристики поперечных сечений брусьев

Пусть швеллер № 20 будет первой фигурой, уголок 100×100×10 мм – второй, а лист 200×10 мм будет третьей

простой фигурой; c = 10 мм. Так как размеры простых сечений 1 и 2 будем брать из сортамента прокатной стали, то в расчетах единицами измерения геометрических величин будут см.

107

В. А. Жилкин

2.11.Конструктор сечений программного комплекса

SCAD OFFICE10

Проектно-вычислительный комплекс SCAD, широко используемый для расчета и проектирования конструкций зданий и сооружений, в последнее время окружен «свитой»

10 SCAD Structure. Формирование сечений и расчет геометрических характеристик. Руководство пользователя / В. С. Карпиловский, Е. З. Криксунов, А. В. Перельмутер, М. А. Перельмутер. К. : ВВП Компас, 2000. 80 с.

108

ГЛАВА2 Геометрические характеристики поперечных сечений брусьев

малых специализированных программ. К их числу принадлежат программы Конструктор Сечений, Консул, Тонкостенные сечения, а также Каталоги сортаментов, которые ориен-

тированы на реализацию проектных процедур, связанных с расчетом элементов стальных конструкций и их соединений. Каждая из этих программ может работать автономно, а все вместе они входят в набор взаимоувязанных по управлению и информации программных средств, который по из-

вестной аналогии называется SCAD Office.

Конструктор Сечений предназначен для формирования произвольных составных сечений из стальных прокатных профилей и листов, а также расчета их геометрических харак-

теристик, необходимых для выполнения расчета конструкций. Элементы пользовательского интерфейса Конструктора

не отличаются от большинства других программ, работающих в среде Windows.

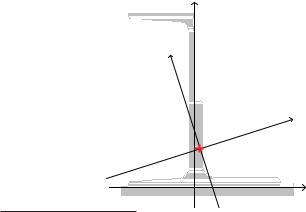
На рис. 2.18 приведён интерфейс рабочего окна программы Конструктор сечений и составное сечение, рассмо-

тренное в примере 2.4.

После активизации кнопки Расчет выполняется расчет геометрических и жесткостных характеристик сечения, появляется диалоговое окно, в котором эти характеристики представлены. Значения характеристик выводятся с назначенной точностью и в установленных для текущего сечения выходных единицах измерения. Нажатие кнопки позволяет сформировать отчет11, содержание которого приводится ниже:

Z

V

U

Y

11 Отчет сформирован программой Конструктор сечений, версия: 11.3.1.1 от 28.02.2009.

109

110

Жилкин .А .В

Рис. 2.18

ГЛАВА2 Геометрические характеристики поперечных сечений брусьев

Габариты 200×210 мм

Геометрические характеристики

111

В. А. Жилкин

Геометрические характеристики

Как следует из приведённой таблицы отчета, величины

геометрических характеристик, вычисленные в примере 2.4 и программой Конструктор Сечений, отличаются незначи-

тельно. Отличие обусловлено тем, что характеристики прокатных профилей взяты из разных ГОСТов и тем, что в SCADе эти характеристики приводятся с двумя или с тремя знаками после запятой. Координаты центра тяжести zC отличаются на единицу, так как в примере 2.4 ось y расположена на нижней поверхности пластины, а в SCADе – на верхней.

112