5.3 Параллельность прямой и плоскости, двух плоскостей

^{Прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (рисунок 25).}

^{Рисунок 25 – Параллельность прямой и плоскости}

^{Рисунок 26 – Параллельность плоскостей}

^{Для построения прямой l (l1, l2), проходящей через точкуK (K2, K1)и параллельной заданной плоскости треугольникаАВС (А1В1С1; А2В2С2) достаточно провести линию, параллельную любой прямой, принадлежащей плоскости. На рисунке 25 показано построениеl (l1; l2)параллельной прямойА1(А111; А212,), лежащей в плоскости АВС (А1В1С1; А2В2С2).}

^{Плоскости параллельны между собой, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. На рисунке 26 построена плоскость θ(ЕD  GF), проходящая через точкуK (K2, K1)и параллельная плоскостиР (CA  AB).Для этого черезК2 проведеныD2Е2‖А2С2, G2F2‖А2В2и черезК1 – D1Е1‖А1С1, G1F1‖A1B1. Таким образом, построенная плоскость (ЕD  GF)будет параллельна заданнойР (CA  AB).}

6 Метрические задачи

^{Задачи, в которых требуется определить величины углов, длин, площадей, называются метрическими. Решение таких задач упрощается, если геометрические образы занимают частное положение относительно плоскостей проекций. В случае, когда объект занимает общее положение возникает необходимость преобразования комплексного чертежа. Наиболее часто применяются при решении задач два способа преобразования чертежа: способ плоско-параллельного перемещения; способ замены плоскостей проекций.}

^{Рисунок 27 – Способ плоскопараллельного перемещения}

^{При применении способа плоско-параллельного перемещения (рисунок 27), важно уяснить следующие основные положения:}

^{1) плоскости проекций неподвижны, а геометрический образ перемещается в пространстве.}

^{2) все точки геометрического образа перемещаются во взаимно-параллельных плоскостях уровня (каждая в своей плоскости).}

^{Если рассматривать плоско-параллельное перемещение, например, прямой, то важно учитывать, что в процессе перемещения она не изменяет угол наклона к той плоскости, относительно которой совершается ее плоско-параллельное перемещение. Отсюда правило, построение комплексного чертежа (рисунок 28):}

^{1) проекция оригинала на плоскости, параллельно которой совершается его движение, сохраняет свою форму и величину, изменяя только положение.}

^{Рисунок 28 – Перемещение прямой}

^{2) проекции точек оригинала на другой плоскости проекций перемещаются по прямым, перпендикулярным соответствующим линиям связи (при этом проекция оригинала на эту плоскость меняет свое положение и форму).}

^{При способе замены плоскостей проекций геометрический образ не изменяет положения в пространстве, а заданная система плоскостей проекций заменяется новой так, чтобы геометрический образ занял частное положение относительно вновь выбранной системы плоскостей проекций.}

^{На рисунке 29 даны проекции точки А (А1, А2), заменим2на4; 4  1; получим новую систему1, 4с новой осьюX14; спроецируем точкуАна4,получимА4.}

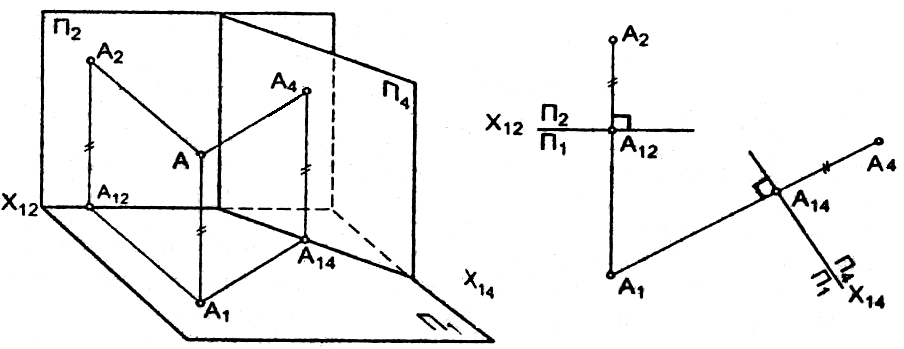
^{а) б)}

^{Рисунок 29 – Способ замены плоскостей проекций}

^{Рассматривая рисунок 29а, видим, что расстояние от А4до новой осиX14 равно расстоянию отА2до старой осиX12, то отрезокZА4 = ZА2.}

^{На комплексном чертеже проводят ось X14 и обозначают новую систему плоскостей проекций1, 4, затем изА1проводят линию связи X14 и на продолжении этой линии связи отА14 откладывают расстояние равное расстоянию от старой проекции точки до старой оси проекции, т.еА2А12.}

^{Получим А4на новой плоскости4; аналогично выполняют построение при1на5(рисунок 29б).}

^{Следует заметить, что при решении различных метрических задач положение новой плоскости проекций определяется в зависимости от поставленной задачи.}