8.6 Построение линии пересечения поверхностей методом вспомогательных секущих плоскостей

^{Задача. Построить линию пересечения полусферы Р и пирамидыQ(рисунок 72)}

^{Рисунок 72 – Пересечение пирамиды и сферы}

1. Задача решается при помощи посредников. За посредники выбираем горизонтальные плоскости уровня. Они пересекают Р по параллелям, а Qпо треугольникам – графически простым линиям.

2. Определяем опорные точки на линии пересечения m. Находим точки пересечения ребер пирамиды с полусферой:M₁,F₁и Е₁. Точку М=SBPнаходим с помощью плоскости(₁) – плоскости главного меридиана полусферы Р. Точки Е иFполучаются в результате пересечения реберASиSCи полусферой Р, найдены точки с помощью плоскости(₂) – плоскость экватора полусферы. Точки М, Е, F являются экстремальными точками, а так же очерковыми на П₂, точки Е и F очерковыми на П₁, и они же точки смены видимости на П₁.

3. Случайные точки определяем с помощью плоскостей уровня (₂) и Г(Г₂);P=n(n₂,n₁) - параллель полусферыQ=l(l₂,l₁) – треугольник DTS; nL=точки 1 и 2. Аналогично с помощью плоскости Г(Г₂) находятся точки 3 и 4.

4. Соединяем найденные точки линии mс учетом видимости.

5. Определяем взаимную видимость Р и Q.

8.7 Построение линии пересечения поверхностей методом вспомогательных концентрических сфер

^{Известно, что если ось поверхности вращения проходит через центр сферы и сфера пересекает эту поверхность, то линия пересечения – окружность, плоскость которой перпендикулярна оси поверхности вращения. При этом если ось поверхности вращения параллельна плоскости проекций, то линия пересечения на эту плоскость проецируется в отрезок прямой линии.}

^{Рисунок 73 – Пересечение сферы с поверхностями вращения}

^{На рисунке 73 показана фронтальная проекция линий пересечения сферой радиуса Rс поверхностями вращения – конусом, тором, цилиндром, сферой, оси которых проходят через центр сферы. Окружности, по которым пересекаются указанные поверхности вращения с поверхностью сферы, проецируется на плоскость в виде отрезков прямых. Это свойство используется для построения линии пересечения двух поверхностей вращения с помощью вспомогательных сфер, но при следующих условиях:}

^{1. Обе поверхности – поверхности вращения}

^{2. Оси поверхностей пересекаются в точке (центр вспомогательных сфер)}

^{3. Плоскость, образованная осями поверхностей (плоскость симметрии) должна быть параллельна плоскости проекции.}

^{Задача.Построить проекции линии пересечения поверхностей цилиндра (Г) и конуса () (рисунок 74).}

^{1. Заданы две поверхности вращения. Оси поверхностей пересекаются. Имеется общая плоскость симметрии ,параллельнаяП2.}

^{2. Линия пересечения – пространственная замкнутая кривая 1-4-3-5-2-5-3-4-1(рисунок 74).}

^{3. Опорные точки: 1, 2– экстремальные; точки3и3– очерковые относительноП1.}

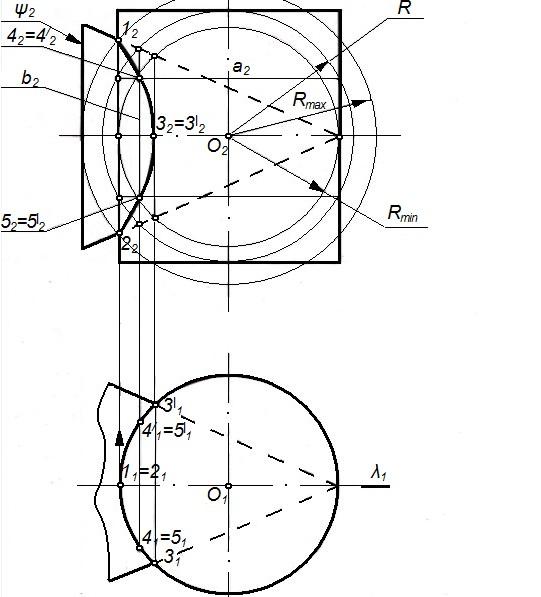
^{Рисунок 74 – Пересечение цилиндра и конуса}

^{4. Промежуточные точки: 4, 4,5, 5найдены с помощью вспомогательной сферы () с центром в точкеО, соосной с заданными поверхностями.}

^{5. Найденные точки соединены плавной кривой с учетом видимости.}