Однополостный гиперболоид вращения

^{На рисунке 51 поверхность имеет две образующие линии l (BC)иl'(B'C')наклоненные в разные стороны и пересекающиеся в толчке(А),принадлежащей наименьшей параллели.}

^{Отрезок ОАявляется кратчайшим расстоянием между образующей и осью. Таким образом, на поверхности однополостного гиперболоида располагаются два семейства прямолинейных образующих. Все образующие одного семейства – скрещивающиеся прямые. Каждая образующая одного семейства пересекает все образующие другого. Через каждую точку поверхности проходят две образующие разных семейств. Меридианом поверхности является гипербола.}

^{Рисунок 51 – Поверхность вращения – однополостный гиперболоид}

7.4 Поверхности, образуемые при вращении окружности Сфера

^{Тело, полученное от вращения полукруга вокруг диаметра, называется шаром, а поверхность, образуемая при этом окружностью, называется сферической (рисунок 52).}

^{Можно также сказать, что эта поверхность есть геометрическое место точек, одинаково удаленных от одной и той же точки, называемой центром. Отрезок, соединяющий центр с какой-нибудь точкой поверхности, называется радиусом, а отрезок, соединяющий две точки поверхности и проходящий через центр, называется диаметром сферы.}

^{На рисунке 52 ось вращения сферической поверхности совпадает с вертикальным диаметром.}

^{Всякая проекция сферической поверхности является окружностью, очерками проекций на плоскость П1является проекция экватора, на плоскостьП2иП3являются проекции меридианов.}

^{Рисунок 52 – Поверхность вращения - сфера}

^{На рисунке 53 отмечены проекции оси i, экватораb, фронтального меридианааи профильногоl.}

^{Задача 1.Построить проекции точекАиВ, принадлежащие сфере рисунок 53.}

^{Недостающие проекции точек, определяются с помощью параллелей, которым эти точки принадлежат.}

^{Видимость точек АиВопределена в зависимости от того, на какой части сферы они лежат (на видимой части – видимы, на невидимой – невидимы).}

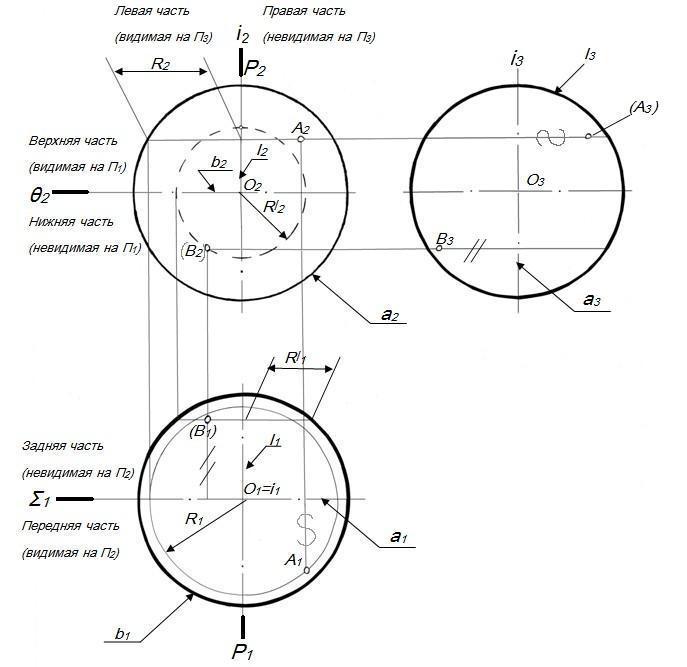
^{Рисунок 53 – Определение видимости сферы}

^{Задача 2. Построить недостающие проекции видимых линий, принадлежащих поверхности сферы.}

^{На рисунке 54а показано построение А1В1С1иА3В3С3по заданнойА2В2С2;L1K1иL3K3по заданнойL2K2;M2N2иM1N1по заданнойM3K3.}

^{На рисунке 54б показано построение А3В3С3D3E3K3по заданнойА2В2С2D2E2K2.}

^а)

^б)

^{Рисунок 54 – Построение линий на поверхности сферы}

Закрытый тор

^{Закрытый тор образован вращением дуги окружности радиуса Rвокруг осиi, расположенной в плоскости окружности, но не проходящий через ее центр, причем ось вращения имеет с окружностью две общие точки (рисунок 55).}

^{Рисунок 55 – Поверхность вращения - закрытый тор}

Открытый тор (круговое кольцо)

^{Открытым тором называется тело, полученное от вращения окружности (образующей) вокруг оси, расположенной в её плоскости, но не проходящей через ее центр, причем ось вращения не имеет общих точек с окружностью (рисунок 56).}

^{Рисунок 56 – Поверхность вращения – открытый тор}

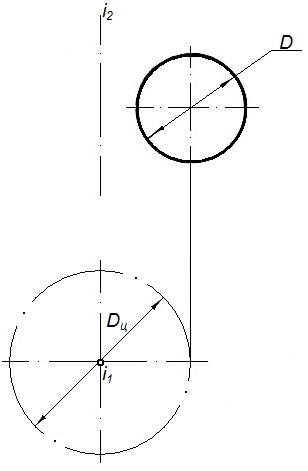
^а)

^б)

^{Рисунок 57 - Комплексный чертеж тора}

^{i– ось кольца(П1) D– диаметр окружности центров образующих окружностей (рисунок 57а). Горизонтальная проекция кольца (рисунок 57б) выразится двумя концентрическими окружностямиDц+DиDс-d. Фронтальная проекция кольца выразится двумя образующими окружностями, сопряженными прямыми.}