Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Конспект_ИЭЭ_14

.pdf

Скачиваний:

Добавлен:

31.03.2015

Размер:

10.55 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 397 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Просуммируем это выражение по всем точкам:

A	A	W		W	W	W
	i	к2i		к1i	к2	к1

Wк

, ч. т. д.

В этом доказательстве мы не делали никаких различий между внешними и внутренними силами и их работами, поэтому подразумевается, что A = Ae + Ai.

1.8.4. Потенциальная энергия материальной точки

Поле (в математике) – величина как функция радиуса-вектора (или координат). Задать силу как функцию радиуса-вектора материальной точки, воздействие на которую описывается этой силой, значит задать силовое поле.

Поле в физике – физический объект (см. РАЗДЕЛ 0.1 и, более подробно, 3.1.1).

Поле потенциально (сила потенциальна), если работа поля при перемещении материальной точки по замкнутой траектории равна нулю (иначе говоря, циркуляция силы по замкнутому контуру равна нулю):

A1 1

Fdl 0

В этом случае работа поля по перемещению материальной точки не зависит от формы её траектории, а зависит только от начального и конечного положения точки.

Доказательство

Пусть в потенциальном поле материальная точка пе-

2ремещается из положения 1 в положение 2 сначала по траектории 1-3-2, а затем по траектории 1-4-2 (РИС. 6.5). Работа по замкнутой траектории 1-3-2-4-1

A	0
13241

Рис. 6.5	по определению потенциального поля. Но, согласно
	определению работы,

A	A	A	A	A
13241	132	241	132	142

A132

A142

, ч. т. д.

Изменением потенциальной энергии материальной точки при перемещении точки из положения 1 в положение 2 называется работа потенциального поля, совершаемая при этом перемещении, взятая с обратным знаком:

Wп12

Aп 12

Потенциальная энергия материальной точки – работа потенциального поля по перемещению материальной точки в данное положение из точки, где потенциальная энергия принята равной нулю, взятая с обратным знаком:

	1		Wп 0
Wп Aп		Fdl	Fdl	.
	Wп 0		1

Физический смысл имеет изменение потенциальной энергии. Сама же по себе потенциальная энергия определяется с точностью до произвольной постоянной. При ответе на вопрос, чему равна потенциальная энергия, нужно обязательно указывать, где выбрано начало её отсчёта (нулевой уровень).

ПРИМЕРЫ РАСЧЁТА РАБОТЫ И ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ

1. Работа силы сухого трения

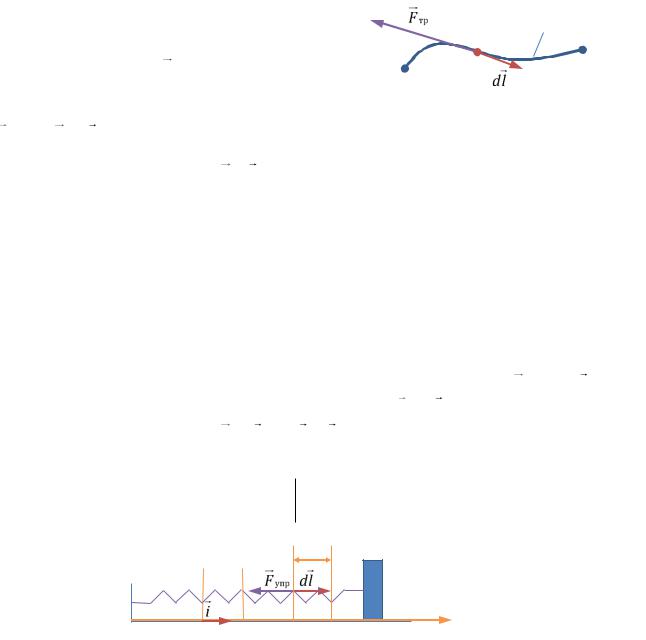
Пусть материальная точка B скользит по шеро-

ховатой плоской поверхности по траектории l,

соединяющей начальную и конечную точки 1 и 2

(РИС. 6.6). Сила трения F тр постоянна по модулю

(Fтр = Fтр max, см. РАЗДЕЛ 1.4.5) и всегда направлена

противоположно элементарному

перемещению

Рис. 6.6

dl , т. е.

Fтр ,dl

π . Элементарная работа

dA Fтрdl Fтрdlcosπ Fтрdl ,

работа при перемещении из точки 1 в точку 2

Fтрdl Fтрl .

Видно, что работа силы трения зависит от длины траектории, соединяющей

начальную и конечную точки, следовательно, сила трения не является потенци-

альной.

2. Работа силы упругости

Пусть пружина жёсткостью k растягивается из состояния с деформацией x1 до де-

формации x2 (РИС. 6.7). В промежуточном положении x сила упругости

упр

kxi

Элементарная работа при увеличении деформации на dl dxi

dA F упрdl kxi dxi kxdx ;

полная работа при растягивании пружины от x1 до x2

kxdx

Рис. 6.7

Эта работа не зависит от того, каким образом пружина переходит от деформации

x1 к деформации x2, значит, сила упругости потенциальна. Изменение потенци-

альной энергии

	A	kx	2	kx	2
W		kx	2	kx	1
W

п12		2		2
		2		2

Положим начало отсчёта потенциальной энергии в положении недеформированной пружины: Wп(0) = 0; при этом потенциальная энергия деформированной пружины

	62

		kx	2
W		kx		.
W
п		2
		2

3. Работа силы тяжести

Пусть материальная точка массы m перемещается из точки 1 в точку 2 по траектории l (РИС. 6.8).

Элементарная работа силы тяжести			Fт mg	на
малом перемещении dl
dA F dl F dlcosα F dh mgdh
т	т	т

(знак «–» появляется из-за того, что изменение высоты отрицательно). Полная работа

1 l

α dh

2 h

	h
	2	2
		2
A		mgdh mg h
	h
	1

h
1

Рис. 6.8

где h1 – высота точки 1 над нулевым уровнем, h2 – высота точки 2. Эта работа не зависит от формы траектории l, а определяется только высотой начального и конечного положений материальной точки массой m, следовательно, сила тяжести потенциальна. Аналогично, любое однородное поле будет потенциальным.

Изменение потенциальной энергии

Wп12

mg h2

h
1

Положим начало отсчёта потенциальной энергии на нулевом уровне: Wп = 0 при h = 0, тогда потенциальная энергия тела массы m в однородном гравитационном поле (поле тяжести)

Wп

mgh

27.

4. Поле центральных сил

Центральная сила – сила, модуль которой зависит только от расстояния от точки, называемой силовым центром, направленная вдоль радиуса-вектора, соединяющего O центр силы с точкой приложения силы:

F f	r	r	.
		r

Пусть материальная точка B движется в поле центральной силы F (силовой центр – точка

1 l

Рис. 6.9

O) от точки 1 к точке 2 по траектории l (РИС. 6.9).Работа силы F

2	2	2
A12 Fdl Fdlcosα Frdr .
1	1	1

Эта величина может зависеть только от r1 и r2, поэтому центральное поле потенциально. Потенциальная энергия

27 Это выражение не является определением потенциальной энергии, как ошибочно полагают многие студенты.

	W 0
	п		r dr
W		F	r dr	.	(6.2)
п		r		.	(6.2)
	r

Частный случай

Гравитационное поле (см. РАЗДЕЛ 1.4.5)

Пусть материальная точка массы m находится в гравитационном поле тела массы M на расстоянии

r от его центра масс (РИС. 6.10). По закону всемир- M  m ного тяготения

F	r	GMm
			2
r		r

Рис. 6.10

G – гравитационная постоянная. Положим начало отсчёта потенциальной энергии в бесконечно удалённой точке: Wп(∞) = 0. Согласно (6.2),

		GMm			GMm
п		GMm		dr	GMm
п			2
W		r			r
	r	r			r
	r

		GMm
		r
		r

1.8.5. Градиент

Из определения потенциальной энергии

dWп dA Fdl	F	dW
	F	п	.
		п
		dl
		dl

Это записывается как

FWп gradWп .

– оператор «набла» – оператор векторного дифференцирования картовых координатах

			i		j		k ,
		x	i	y	j	z	k ,
		x		y		z
	– частная производная функции трёх переменных x, y, z по x и т. д.
x
x

	d

	dl

, в де-

Градиент – произведение вектора на скалярную функцию – векторная функция скалярного аргумента; в декартовых координатах

gradW W		W	i	W
gradW W		п	i	п
		п		п
п	п	x		y
		x		y

	j	W
	j	п
		п
		z

(6.3)

Направление градиента совпадает с направлением наиболее быстрого возрастания скалярной функции. Из II закона Ньютона


F ma,
	a
F gradW
	п

gradW
п

(здесь a – ускорение материальной точки, m – её масса). Материальная точка ускоряется в направлении, противоположном градиенту потенциальной энергии.

В точках, где grad Wп = 0, a 0 и материальная точка находится в положении рав-

новесия. Устойчивое равновесие имеет место в точках, соответствующих минимуму потенциальной энергии.

ПРИМЕР

Дана зависимость потенциальной энергии материальной точки в некотором поле от декартовых координат: Wп = axyz, где a – постоянная. Найти силу, с которой поле действует на материальную точку, как функцию координат.

Из (6.3) получим

	W		i	W	j	W		a yzi xz j xyk .
F gradWп		п		п		п	k

		x		y		z
Видно, что F 0	в любой точке на всех трёх осях декартовой системы координат –

там имеет место равновесие (устойчивое при a > 0 и неустойчивое при a < 0).

1.8.6. Потенциальная энергия механической системы

Если механическая система находится во внешних потенциальных полях, а также взаимодействие тел, входящих в эту систему, описывается потенциальными силами, то можно характеризовать состояние системы потенциальной энергией.

Потенциальная энергия механической системы равна работе внешних и внут-

ренних потенциальных сил при переходе системы из данной конфигурации в конфигурацию, где потенциальная энергия системы принята равной нулю (конфигурация системы – это совокупность координат тел (материальных точек), входящих в эту систему):

W	A	0	A	0	.
п	W	0	W	0	.
	п		п

ПРИМЕР

Потенциальная энергия системы двух гравитирующих тел

Рассмотрим систему из двух тел массами M и m, взаимодействующих гравитационно. Расстояние между центрами масс этих тел равно r (РИС. 6.10). Найти потенциальную энергию системы.

Единственная сила, которая здесь учитывается, гравитационная сила – внутренняя и ПОТЕНЦИАЛЬНАЯ. Положим начало отсчёта потенциальной энергии в бесконечно удалённой точке: Wп(∞) = 0. Найдём работу гравитационной силы при удалении тела массой m (или тела массой M) в бесконечность. Она будет равна потенциальной энергии системы

			F r dr		GMm			GMm

W A							dr
						2
п	r				r			r
		r		r					r

здесь G – гравитационная постоянная.

		GMm
		r
		r

Лекция 7

1.8.7. Закон сохранения и изменения механической энергии

Рассмотрим механическую систему; тела, входящие в эту систему, претерпевают внешние и внутренние воздействия, описываемые потенциальными и непотенциальными силами, и конфигурация системы изменяется. Изменение кинетической энергии системы (см. РАЗДЕЛ 1.8.3) равно сумме работ внешних и внутренних сил:

Wк

Ae п

Ae нп

Ai п

нп

где Ae п – сумма работ внешних потенциальных сил, Ai нп – сумма работ внутренних непотенциальных сил и т. п. Перенесём работу потенциальных сил в левую часть этого равенства:

W A	A
e п	i п
к

Wп

В левой части равенства (7.1) стоит сумма альной энергии системы. Введём величину

W W
к

e нп	i нп	.	(7.1)
A	A

изменений кинетической и потенци-

Wп

– механическая энергия системы – сумма кинетической и потенциальной энергии. Соответственно левая часть уравнения (7.1) равна изменению механической энергии системы. Т. е.

W A	A
e нп	i нп

– закон изменения механической энергии системы: изменение механической энергии системы равно сумме работ внешних и внутренних непотенциальных сил.

Закон сохранения механической энергии: механическая энергия системы не из-

меняется с течением времени, если сумма работ внешних и внутренних непотенциальных сил равна нулю, а все внешние потенциальные силы стационарны (т. е. не зависят явным образом от времени).

Консервативные силы – потенциальные силы и непотенциальные силы, работы которых равна нулю.

Диссипативные силы – непотенциальные силы, работа которых меньше нуля.

При наличии взаимодействий, описываемых диссипативными силами, происходит диссипация энергии – переход механической энергии в другие виды энергии.

Демонстрации: 1) Маятник Максвелла 2) «Мёртвая петля»

1.9. Удар

1.9.1. Абсолютно неупругий удар

Абсолютно неупругий удар – удар, после которого соударяющиеся тела движутся как единое целое.

При неупругом ударе импульс системы соударяющихся тел сохраняется, а механическая энергия – нет. Происходит диссипация энергии.

Рассмотрим абсолютно неупругое центральное соударение двух шаров. (Цен-

тральное соударение – соударение, перед которым центры шаров движутся по прямой, их соединяющей.) Массы шаров равны m1 и m2, их скорости до соударения

– соответственно v1

и v2

(РИС. 7.1). Найдём скорость

шаров после удара.

До удара:	m1	m2
До удара:
После удара:		m1 + m2	x
		m1 + m2

		Рис. 7.1
Закон сохранения импульса:
		m1 v1 m2 v2 m1 m2 u .

Спроецируем это равенство на ось x (вдоль направления движения шаров):

m1v1x m2v2x m1 m2 ux .

Отсюда получим

ux	m v		m v		.
	1	1x	2	2x

		m m
		1	2

В этой формуле содержится информация о модуле и о направлении скоростей ша-

ров;

Найдём долю η механической энергии, перешедшей во внутреннюю при ударе:

к1

к2

к1

здесь Wк1 – кинетическая энергия системы до удара, Wк2 – после удара, Wк – из-

менение кинетической энергии при ударе;

m v2

2 ,

к1

m m

m v

1 2

1 1x

2 2x

1 1x

2 2x

к2

2 m m

2 m1 m2

m v

η 1

1 1x

m m

m v

Если шары до соударения двигались в одну сторону, то v1x = v1, v2x = v2 и

	2	2			2				2		2	2		2	2	2m m v v					2	2
η	m v		m m v			m m v				m v			m v								m v
	1	1	1	2	2		1	2	1		2	2		1	1	2	1	2	1	2	2	2
										2			1
								1				1			2
							m m						2			2
											m v			m v

	m
	m
	1

m m		v		v		2

1	2		1	1	2	2	2
2			1
m				2			2
			m v		m v

Если же шары двигались в разные стороны, то

	m m		v	v	2
η	1	2	1	2		.
η	m1 m2 m1v12 m2v22					.

При v2 = 0

η	m
η	2
	2
	m m
	1	2

1.9.2. Абсолютно упругий удар

Абсолютно упругий удар – удар, при котором соударяющиеся тела испытывают упругую деформацию.

При абсолютно упругом ударе сохраняется и импульс, и механическая энергия системы соударяющихся тел.

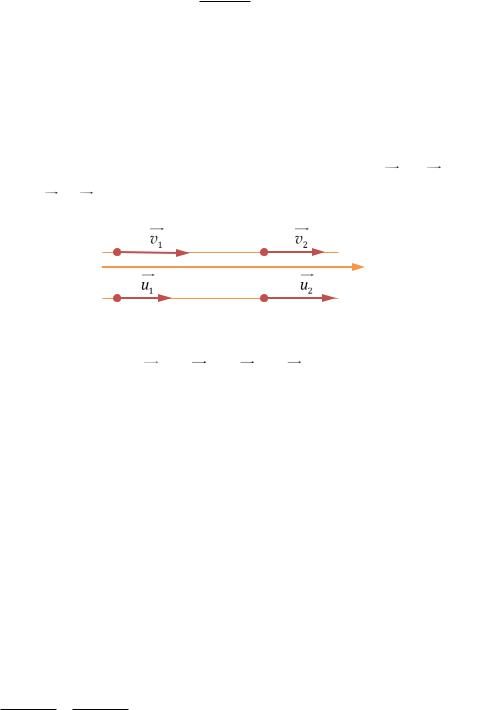
Рассмотрим абсолютно упругое центральное соударение двух шаров. Массы шаров равны m1 и m2, их скорости до соударения – соответственно v1 и v2 (РИС. 7.2).

Найдём скорости u1	и u2	шаров после удара.
До удара:		m1	m2
До удара:
После удара:		m1	m2	x
		m1	m2

Рис. 7.2

Закон сохранения импульса:

m1 v1 m2 v2 m1u1 m2u2

Закон сохранения механической энергии:

m v		2	m v		2		2		2
						m u		m u
1	1		2	2		1	1	2	2

2			2			2		2

(7.2)

(7.3)

Спроецируем векторное равенство (7.2) на ось x (вдоль направления движения

шаров), преобразуем уравнение (7.3) (подставим				2		2	и т. п.) и запишем систе-
шаров), преобразуем уравнение (7.3) (подставим				v1	v1x		и т. п.) и запишем систе-
му уравнений
m v	m v	m u	m u			,
1 1x	2 2x	1 1x		2	2x
	m v2	m u2	m u2 .
m v2	m v2	m u2	m u2 .
1 1x	2 2x	1 1x		2	2x

Решим эту систему самым быстрым способом:


m v				m u		m u		m v			,
	1	1x		1	1x	2	2x	2	2x
			2		2		2	m v		2	;
m v				m u		m u		m v			;
	1	1x		1	1x	2	2x	2	2x

затем разделим нижнее уравнение на верхнее и исключим u2x:

v	u	v	u
2	2	2	2
1x	1x	2x	2x
1x	1x	2x	2x
v	u	v	u
1x	1x	2x	2x

v1x u1x v2x u2x

u2x

v1x

v2x

u1x

	m1v1x m1u1x m2v1x m2v2x m2u1x m2v2x ,
	m1v1x m2v1x 2m2v2x		m1 m2 u1x ,
u	m1 m2 v1x 2m2v2x	, u		m2 m1 v2x 2m1v1x	.	(7.4)

1x		2x		m1 m2
	m1 m2

Частные случаи

1. Упругое соударение шаров одинаковой массы

При m1 = m2 = m из (7.4) получим

u1x v2x , u2x v1x .

Соударяющиеся тела обмениваются скоростями.

2. Удар шара об упругую плиту

Масса плиты намного больше массы шара (m2 >> m1); в лабораторной системе отсчёта плита покоится (v2 = 0). Из

(7.4) получим
0	m
	m		1		v
		1	1		v
		m			1x
u1x		m			v1x
		2				(РИС. 7.3).
		m				(РИС. 7.3).
		m		1
			1	1
			1
		m
			2
				0		Рис. 7.3

Демонстрация: Удары шаров

1.10. Повторение: Поступательное и вращательное движение

Цель данного параграфа – обобщение материала, касающегося механики точки (поступательного движения твёрдого тела) и вращения твёрдого тела вокруг неподвижной оси, который отрабатывается на практических занятиях в I семестре.

1.10.1.Сравнение физических величин и законов поступательного и

вращательного движения

Величина / закон

Перемещение

Скорость

Ускорение

Таблица 7.1

Поступательное движение				Вращательное движение
Перемещение r				Угловое перемещение			φ
Скорость					Угловая скорость
v	dr				ω	dφ
v	dt				ω	dt
	dt					dt
Ускорение					Угловое ускорение
a dv	d2r				ε dω	d2φ
dt	dt2				dt	dt2

		v ωr
	a εr		ω ωr

Таблица 7.1 (продолжение)

Величина / закон	Поступательное движение
Закон движения	r r			t
Закон движения
Частные случаи:
Равномерное	v const
движение	r t r			vt
			0
Равноускоренное	a const
Равноускоренное	r t r0 v0t at2
движение	r t r0 v0t at2
					2
Мера инертности	Масса m
Мера взаимодействия	Сила			F
Мера инертности и	Импульс
Мера инертности и
движения	p mv
Основной закон
Основной закон
динамики	dp	F
в дифференциальной	dt	F
в дифференциальной	dt
форме
	Условие сохранения
Условие сохранения	импульса
Условие сохранения
	P const	при F 0
Элементарная работа	dA Fdr
Кинетическая энергия	W mv2
	к			2
				2
1.10.2. Методы решения задач по механике
	Методы решения задач

Вращательное движение

φφ t

ωconst

φ t φ0 ωzt

ωconst

φt φ0 ω0zt εz2t2

Момент инерции I

Момент силы M

Момент импульса

	L Iω
	dL	M
	dt

Условие сохранения момента импульса

L const при		M 0
dA Mdφ
	2
W	Iω
W
к	2
	2

через основной закон динамики

Найти: t, , , …

Важно знать закон изменения искомой величины со временем.

через законы сохранения

Найти: v, ω, S, …

Важно знать характеристики начального и конечного состояния системы, процесс перехода от начального к конечному состоянию не имеет значения.

<<< < Предыдущая 1 2 3 4 5 67 / 397 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.03.201590.73 Кб23КоммуникацияЛекция.docx
#
31.03.20153.47 Mб19Конс по УП 2013 (12 лекций).pdf
#
31.03.20154.34 Mб306Конспект лекций (Цифровая техника) 2013.doc
#
13.03.20163.73 Mб233Конспект лекций_ФИЗИКА_2сем.pdf
#
31.03.20151.2 Mб690конспект.pdf
#
31.03.201510.55 Mб94Конспект_ИЭЭ_14.pdf
#
31.03.2015289.21 Кб36КОНСТР_ТР_6.docx
#
21.09.2019767.55 Кб5контролинг_итог.docx
#
23.09.201921.23 Кб5Концепция научного менеджмента.docx
#
31.03.20153.97 Mб12КП2.pdf
#
10.11.201934.66 Кб20кПр 2.docx