
Конспект_ИЭЭ_14
.pdf
|
|
170 |
Для анизотропных диэлектриков |
D |
и E не параллельны. Диэлектрические свой- |
ства вещества определяются тензором диэлектрической проницаемости
|
ε |
|
|
ε |
|
|
||
|
||
|
ε |
|
|
||
|
xx yx zx
ε ε ε
xy yy zy
ε |
|
|
|
xz |
|
ε |
|
|
yz |
||
|
||
ε |
|
|
zz |
||
|
и
|
ε |
|
ε |
|
ε |
E |
|
|
|
xx |
|
xy |
|
xz |
x |
D ε0 |
εyx |
εyy |
εyz Ey . |
||||
|
εzx |
εzy |
|
|
|
||
|
εzz Ez |
||||||
ПРИМЕР
Поле точечного заряда в однородном диэлектрике
Точечный заряд Q > 0 находится в безграничном диэлектрике с относительной диэлектрической проницаемостью ε (РИС. 21.4). Найдём ряд векторных характеристик электрического поля, создаваемого этим зарядом.
 S
S
ε
Q |
|
r |
|
A |
|
|
|
Рис. 21.4
охваченный заряд q |
S |
|
Связь между D |
и E : |
Так как в пространстве имеется диэлектрик, воспользуемся теоремой Остроград-
ского-Гаусса для D
|
DdS q |
S |
. |
|
|
||
S |
|
|
|
Выберем поверхность интегрирования S в виде сферы радиуса r – расстояние от заряда Q до точки A, в которой исследуется поле, с центром в точке, где расположен
заряд Q; нормаль dS направлена радиально, как и D . Поток D
DdS Dr 4πr2 ,
S
Q . Получим |
|
|
||
D 4πr2 |
Q, D |
Q |
. |
|
4πr2 |
||||
r |
r |
|
||
D ε |
εE |
0 |
|
Dr
ε εE |
r |
0 |
,
Er
|
D |
|
Q |
|
|
r |
|
|
|
||
|
|
|
|
|
|
|
ε ε |
|
4πε |
εr |
2 |
|
|
|
|||
|
0 |
|
0 |
|
|
.
Поляризованность, исходя из определения
D
(21.5),
P D ε0 E
P D ε E |
|
|
Q |
|
|
ε Q |
|
||
|
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
r |
r |
0 |
r |
|
4πr |
2 |
|
4πε εr |
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
|
Q |
|
4πr |
2 |
|
|
1 |
|
1 |
|
|
ε |
|
||
|
|
|
|
.
Найдём также напряжённость электрического поля свободных и связанных зарядов. Проекция напряжённости электрического поля свободных зарядов на радиальное направление (см. 3.2.2)

171
E0r
|
Q |
|
|
4πε r |
2 |
||
|
|||
|
|
||
|
0 |
|
.
Так как E E0 E , напряжённость электрического поля связанных зарядов
E E |
|
E |
|
|
Q |
|
|
Q |
|
|
Q |
|
|
1 |
1 |
|
0 |
r |
0r |
|
2 |
|
2 |
|
2 |
|
|
|
|||||||
r |
|
|
4πε εr |
|
4πε r |
|
4πε r |
ε |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
|
|
0 |
|
|
0 |
|
|
|
|
– поле связанных зарядов направлено против поля свободных зарядов. Отношение
E |
r |
|
1 |
1 |
|
|
|
|
|||
|
|
|
|
|
|
E |
0r |
|
ε |
|
|
|
|
|
|
||
– диэлектрик ослабляет электрическое поле свободных зарядов в ε раз. Демонстрация: Изменение потенциала при вводе диэлектрической пластины
4. Теорема Остроградского-Гаусса в дифференциальной форме
Дивергенция
divE E
– скалярная функция векторного аргумента. В декартовых координатах
divE |
E |
x |
|
E |
y |
|
E |
z |
; |
|
|
|
|
||||||||
x |
y |
z |
||||||||
|
|
|
|
|||||||
в сферических координатах
divE |
1 |
|
2 |
|
|
|
1 |
|
|
E |
|
sinθ |
|||||
r |
2 |
r |
r E |
r |
r sinθ θ |
θ |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
в цилиндрических координатах |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
divE |
1 |
rEr |
1 Eφ |
|
Ez |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
r r |
r |
φ |
z |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
1 |
Eφ |
r sinθ φ |
|
.
;
Можно доказать, что из теоремы Остроградского-Гаусса в интегральной форме (21.4), (21.5), (21.7) следует теорема Остроградского –Гаусса в дифференциальной форме:
PdS q S
S
divP ρ
,
(21.8)
DdS q S
S
divD ρ
,
EdS q S |
q S |
S |
ε0 |
divE |
ρ ρ |
|
ε |
||
|
||
|
0 |
.

172
ПРИМЕР
Расчёт объёмной плотности связанных зарядов (см. ПРЕДЫДУЩИЙ ПРИМЕР)
Точечный заряд Q находится в безграничном диэлектрике относительной диэлектрической проницаемостью ε. Найти объёмную плотность связанных зарядов в диэлектрике как функцию от расстояния r от заряда Q.
РАНЕЕ была получена зависимость поляризованности от r:
P |
r |
r |
|
Q |
|
4πr |
2 |
|
|
1 |
|
|
||
|
|
|
1 ε
.
Рассчитаем объёмную плотность связанных зарядов по теореме ОстроградскогоГаусса для P в дифференциальной форме (21.8):
|
|
1 d |
2 |
|
1 d |
|
r2Q |
|
|
1 |
|
|||||||||
ρ |
divP |
|
|
|
|
r |
Pr |
|
|
|
|
|
|
|
|
1 |
|
|
|
0 . |
r |
2 |
|
dr |
r |
2 |
|
|
4πr |
2 |
ε |
||||||||||
|
|
|
|
|
|
|
|
dr |
|
|
|
|
|
|
||||||

173
Лекция 22
3.3.3. Электрическое поле в диэлектриках (продолжение)
5. Условия на границе раздела двух диэлектриков
Проанализируем, как изменяется электрическое поле при переходе из одной среды (диэлектрика) в другую.
Пусть имеются два изотропных диэлектрика (относительные диэлектрические проницаемости ε1 и ε2), граничащие друг с другом (РИС. 22.1). В среде с ε1 суще-
ствует электрическое поле с напряжённостью E1 и электрическим смещением
D1
. Свободные заряды на границе раздела сред отсутствуют. Найдём векторные
характеристики поля в среде с ε2 – E2 |
и |
D2 |
тельную τ к поверхности раздела сред). |
|
|
(в проекциях на нормаль n и каса-
ε1 |
|
ε1 |
1 |
2 |
|
|
|
|
|
ε2 |
|
ε2 |
4 |
3 |
S |
|
|
|
L |
а |
|
|
|
б |
|
Рис. 22.1 |
|
|
|
1) Dn
Воспользуемся теоремой Остроградского-Гаусса для
|
DdS q |
S |
. |
|
|
||
S |
|
|
|
D
Выберем поверхность интегрирования S в виде цилиндра, основания которого параллельны границе раздела сред, а высота мала (РИС. 22.1А). Поток D
|
DdS D |
S |
торц |
|
|
DdS D |
S |
торц |
|
|
1n |
|
|
|
2n |
|
|
||||
S |
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
бок |
|
|
|
|
|
охваченный поверхностью S заряд q 0S 0 , так |
||||||||||
нице раздела отсутствуют. Поэтому |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
D |
|
|
|
|
|
|
|
|
|
2n |
1n |
|
|
|
D2n D1n Sторц ;
как свободные заряды на гра-
(22.1)
– нормальная составляющая вектора электрического смещения не претерпевает скачка на границе раздела диэлектриков.
2) En
Связь D
поэтому
и
E
в изотропном диэлектрике
D ε0εE ,

174
D1n ε0ε1E1n , D2n ε0ε2E2n .
С учётом условия (22.1)
ε0ε1E1n ε0ε2E2n |
E |
|
|
ε |
|
2n |
1 |
||
|
|
|||
E |
|
|
ε |
|
|
1n |
|
||
|
|
|
2 |
(22.2)
– нормальная составляющая напряжённости электрического поля претерпевает скачок на границе раздела диэлектриков.
3) Eτ
Воспользуемся I уравнением Максвелла – условием потенциальности электростатического поля
Edl 0.
L
Выберем контур интегрирования L в виде прямоугольника, одна пара сторон которого параллельная границе раздела сред (стороны 1-2 и 3-4 на РИС. 22.1Б), а дру-
гая мала (стороны
L
2-3 и 4-1).
Edl E |
l |
|
1τ 12 |
Циркуляция
|
3 |
|
|
|
|
|
|
|
Edl E |
|
l |
||
|
|
|
2τ |
34 |
||
|
2 |
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
E |
2τ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E
E
по контуру L
1 |
Edl E |
|
|
|
l |
|
|
1τ |
E |
2τ |
|||
|
|
|
12 |
|||
4 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1τ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0
,
(22.3)
– тангенциальная составляющая напряжённости электрического поля не претерпевает скачка на границе раздела диэлектриков.
4) Dτ
Из связи между
D
и
E
и условия
D |
ε ε |
E |
1τ |
0 1 |
|
(22.3) получим
1τ , D2τ ε0ε2E2τ
D2τ ε2
D1τ ε1
D |
|
D |
, |
|
1τ |
2τ |
|||
|
|
|||
ε |
|
ε |
|
|
1 |
|
2 |
|
(22.4)
– тангенциальная составляющая электрического смещения претерпевает скачок на границе раздела диэлектриков.
3.3.4. Проводники в электростатическом поле
Свойства электростатического поля в проводниках55
1.Внутри проводника напряжённость электрического поля равна нулю:
Eвнутри 0.
В противном случае по проводнику будет идти ток, так как в проводнике имеются свободные заряды, свободно перемещающиеся под действием электрического поля.
Демонстрация: Клетка Фарадея
55 Следует отметить, что эти утверждения относятся только к электростатическому полю в проводниках, т. е. к случаю, когда электрический ток отсутствует.

175
2.Напряжённость электрического поля перпендикулярна поверхности проводника:
Eτ
0
,
E En
.
Если Eτ ≠ 0, то по поверхности проводника будет идти ток.
3.Нескомпенсированный заряд располагается на поверхности проводника:
ρ0 .
Доказательство
Проведём внутри проводника произвольную замкнутую поверхность S (РИС. 22.2). Теорема Остроградского-Гаусса для D
|
|
|
|
|
DdS q |
S |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
Но |
D 0 |
, так как |
E 0 |
, |
поэтому DdS 0 |
и |
q |
S |
0 |
, т. е. |
||
S
нескомпенсированного заряда внутри проводника нет.
 S
S
Рис. 22.2
Демонстрация: Стекание заряда с острия 4. Поверхность проводника эквипотенциальна (а также весь объём проводника):
φ const
.
Доказательство |
|
|
Найдём разность потенциалов между точками 1 и 2 на одном |
2 |
|
проводнике, соединив эти точки кривой, целиком лежащей внут- |
||
|
||
ри проводника (РИС. 22.3), и воспользовавшись интегральной свя- 1 |
|
|
зью напряжённости и потенциала электростатического поля: |
|
12 |
|
2 |
|
|
|
Edl 0 |
|
φ |
|
||
|
|
1 |
|
φ1
φ2
, ч. т. д.
Рис. 22.3
Демонстрация: Распределение заряда на поверхности проводника
5.Нормальная проекция электрического смещения у поверхности проводника равна поверхностной плотности свободных зарядов:
Dn
Доказательство
σ
.
Применим теорему Остроградского-Гаусса для D , выбрав поверхность интегрирования S в виде цилиндра, одно из оснований которого лежит внутри проводника, а другое плотно прилегает к поверхности проводника с внешней стороны (РИС. 22.4):
|
DdS q |
S |
; |
|
|
||
S |
|
|
|
DdS DnSторц ,
S
S
Рис. 22.4
так как внутри проводника D 0 ме внешнего торца, равны нулю;
и потоки D через все стороны цилиндра S, кро-
q S σSторц ,

176
так как заряд распределён только по поверхности проводника;
D S |
торц |
σS |
торц |
n |
|
Dn
σ
, ч. т. д.
3.4. Электрическая ёмкость
3.4.1. Ёмкость уединённого проводника
Уединённый проводник – проводник, удалённый от других тел, так что влиянием их электрических полей можно пренебречь.
Рассмотрим, как изменяются напряжённость электрического поля и потенциал уединённого проводника при изменении его заряда. При увеличении заряда в n раз напряжённость поля и потенциал увеличатся также в n раз (см.
ДЕЛЕ 3.2.4).
Электрическая ёмкость уединённого проводника – характеристика проводни-
ка, равная отношению заряда проводника к его потенциалу:
C |
Q |
|
φ |
||
|
||
|
|
, C Ф (фарад).
Ёмкость не зависит от заряда, потенциала и прочих характеристик электрического поля, она зависит от формы и размеров проводника и диэлектрических свойств среды, его окружающей.
ПРИМЕР
Ёмкость шара
Уединённый проводник – металлический шар радиуса R находится в вакууме (РИС. 22.5). Найти ёмкость проводника.
Q
O R
r
A
Рис. 22.5
SМысленно зарядим проводник зарядом Q и рассчитаем потенциал проводника (потенциал отсчитывается от бесконечно удалённой точки).
Сначала найдём напряжённость электрического поля из теоремы Остроградского-Гаусса для E :
|
q |
|
|
|
|
EdS |
|
S |
|
ε |
. |
S |
|
|
0 |
|
Поверхность интегрирования S – сфера радиуса r, где r
– расстояние от центра шара до точки, где измеряется поле, концентричная заряженному шару. Поток E
EdS Er 4πr |
2 |
|
|
S |
|
(см. ПРИМЕР 1) В РАЗДЕЛЕ 3.2.3), охваченный заряд равен заряду шара Q;
E |
4πr |
2 |
|
Q |
|
||||
|
|
|||
r |
|
|
|
ε |
|
|
|
|
|
|
|
|
|
0 |
Er |
Q |
|
|
. |
|
4πε r2 |
||
|
0 |
|
Потенциал шара найдём из интегральной связи напряжённости и потенциала электростатического поля:
R |
|
R |
|
|
|
R |
|
|
|
φ Erdr |
Q |
dr2 |
Q 1 |
|
Q |
. |
|||
|
|
|
|
||||||
4πε |
4πε r |
4πε R |
|||||||
|
|
r |
|
|
|||||
0 |
|
0 |
|
0 |
|
||||

177
По определению ёмкости
C |
Q |
|
φ |
||
|
4πε |
R |
0 |
|
.
3.4.2. Взаимная ёмкость двух проводников |
|
|
|||||
Рассмотрим систему, состоящую из двух проводников, заря- |
|
–q |
|||||
ды которых равны по модулю и противоположны по знаку q |
|||||||
|
|||||||
(РИС. 22.6). Разность потенциалов между проводниками про- |
|
|
|||||
порциональна модулю их заряда: φ+ – φ– ~ q. Отношение |
φ+ |
φ– |
|||||
|
|
|
|
|
|||
|
C |
|
q |
|
|
|
|
|
|
|
|
Рис. 22.6 |
|||
|
φ φ |
|
|
||||
|
|
|
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
– взаимная ёмкость проводников. Эта величина зависит от размеров, формы, взаимного расположения проводников и диэлектрических свойств среды и не зависит от заряда, потенциала и прочих характеристик электрического поля.
3.4.3. Конденсаторы
Конденсатор – система двух проводников, расположенных настолько близко друг к другу, что, если этим проводникам сообщить одинаковые по модулю, но разные по знаку заряды, электрическое поле будет в основном сосредоточено между этими проводниками – обкладками конденсатора. Модуль заряда каждой из обкладок – заряд конденсатора.
Ёмкость конденсатора – характеристика конденсатора, равная отношению заряда конденсатора к модулю разности потенциалов между его обкладками (напряжению на обкладках):
C |
|
Q |
|
|
Q |
|
φ |
|
φ |
U |
|||
|
|
|||||
|
|
|
|
|
|
.
(22.5)
Ёмкость конденсатора зависит от формы и размеров обкладок, их взаимного расположения, диэлектрических свойств среды между обкладками и не зависит от заряда, напряжения и т. п.
Для расчёта ёмкости любого конденсатора нужно мысленно придать ему заряд, найти напряжение между обкладками, а затем ёмкость по определению (22.5).
В ТАБЛИЦЕ 22.1 представлены конденсаторы простейшей формы и стандартные формулы56 для вычисления их ёмкости. Примеры вывода подобных формул даны
НИЖЕ.
56 Эти формулы относятся к конденсаторам, пространство между обкладками которых заполнено однородным диэлектриком с относительной диэлектрической проницаемостью ε. В других случаях формулы для вычисления ёмкости нужно выводить заново, пользуясь определением ёмкости.
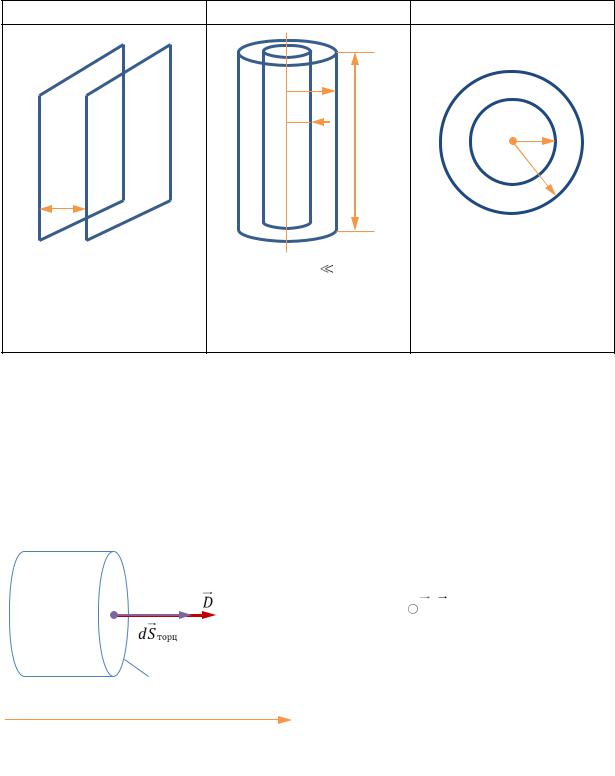
Плоский
ε
S
d
d << размеров пластин
C |
ε εS |
|
0 |
||
|
||
|
d |
ПРИМЕРЫ
178
Конденсаторы
Цилиндрический
R2
εR1
l
R |
R |
l |
2 |
1 |
|
C |
2πε εl |
|
|
0 |
|
|
|
|
|
ln |
R |
|
2 |
|
|
|
|
|
|
R |
|
|
1 |
Таблица 22.1
Сферический
ε O R1
R2
C |
4πε εR |
R |
||
0 |
1 |
2 |
||
|
||||
|
R R |
|
||
|
2 |
1 |
||
1) Расчёт ёмкости плоского конденсатора, заполненного однородным диэлектриком
Имеется плоский конденсатор, площадь обкладок которого равна S, расстояние между обкладками – d, пространство между обкладками заполнено диэлектриком с относительной диэлектрической проницаемостью ε (РИС. 22.7). Найти ёмкость конденсатора.
Q |
ε |
–Q |
|
|
Зарядим обкладки конденсатора заря- |
|||||||
|
|
дом Q. Найдём электрическое смещение |
||||||||||
|
|
|
|
|||||||||
|
|
|
|
|
в пространстве внутри конденсатора с |
|||||||
|
|
|
|
|
помощью |
|
теоремы |
Остроградского- |
||||
|
|
|
|
|
Гаусса |
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
DdS q |
S |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
здесь q |
S |
– сумма свободных зарядов, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
охваченных |
поверхностью S. |
Поверх- |
|||||
|
|
|
|
ность интегрирования S выберем в виде |
||||||||
|
|
|
|
|
||||||||
|
|
d |
|
x |
цилиндра, основания |
которого |
парал- |
|||||
0 |
|
|
лельны обкладкам конденсатора, один |
|||||||||
|
|
|||||||||||
|
|
|
|
|||||||||
Рис. 22.7 |
из торцов располагается вне конденса- |
|
тора (за положительно заряженной об- |
||
|
кладкой), а другой – внутри конденсатора. Вне конденсатора поле отсутствует (это легко показать с помощью принципа суперпозиции полей, воспользовавшись
результатом РАСЧЁТА ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОЙ ПЛОСКОСТИ), внутри конденса-
тора оно однородно;

179
DdS
S
D S |
торц |
x |
,
q |
S |
|
σSторц
,
σ – поверхностная плотность заряда положительно заряженной обкладки,
σQ S
.
Заметим, что легко найти поток D |
мы можем благодаря тому, что пластины счи- |
таются большими, т. е. практически бесконечными – мы пренебрегаем краевыми эффектами. Получим
Dx σ |
Q |
. |
|
S |
|||
|
|
Далее, найдём напряжённость электрического поля через связь
D
и
E
D ε |
εE |
0 |
|
E
x
|
D |
|
Q |
x |
|
||
|
|
|
|
|
ε ε |
|
ε εS |
|
0 |
|
0 |
.
Затем найдём разность потенциалов между обкладками конденсатора, воспользовавшись интегральной связью напряжённости и потенциала электростатического поля:
|
|
φ 0 φ d |
0 |
|
|
0 |
Q |
|
Qd |
|||
|
|
|
x |
dx |
|
dx |
||||||
U φ |
φ |
|
E |
|
ε εS |
ε |
εS |
|||||
|
|
|
|
|
d |
|
|
d |
|
|||
|
|
|
|
|
|
|
0 |
|
0 |
|
||
Наконец, по определению ёмкости (22.5) |
|
|
|
|
|
|
|
|
|
|||
|
|
C |
Q |
|
ε εS |
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
d |
|
|
|
|
|
|
– формула, приведённая в ТАБЛ. 22.1. Демонстрация: Плоский раздвижной конденсатор
.
2) Расчёт ёмкости воздушного коаксиального кабеля (цилиндрического конденсатора)
Имеется воздушный коаксиальный кабель (в пространстве между обкладками ε = 1), радиусы обкладок равны R1 и R2 (РИС. 22.8). Найти ёмкость кабеля, приходящуюся на отрезок единичной длины.
Ход решения будет аналогичен ПРЕДЫДУЩЕМУ ПРИМЕРУ. Зарядим обкладки линей- τ –τ ными плотностями τ (внутреннюю обкладку) и –τ (внешнюю обкладку). Так как между обкладками нет диэлектрика, мож-
h |
r |
но обойтись без |
D |
. Теорема Остроградско- |
|
|
|||||
|
го-Гаусса для E |
|
|
||
|
|
A |
|
|
|
|
|
EdS q S . |
|||
|
|
|
|||
|
|
|
|||
|
|
S |
S |
|
ε0 |
|
|
Поверхность интегрирования S выберем в |
|||
|
|
|
|||
|
|
|
виде цилиндра, коаксиального (соосного) |
||
|
|
Рис. 22.8 |
кабелю, произвольной высоты h, много |
||
|
|
|
меньшей длины кабеля, радиуса r, где r – |
||
расстояние от оси кабеля до точки, в которой измеряется поле. Внутри внутреннего провода (при r < R1) и вне кабеля (при r > R2) поля нет.
