Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Конспект_ИЭЭ_14

.pdf

Скачиваний:

Добавлен:

31.03.2015

Размер:

10.55 Mб

Скачать

☆

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 3919 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

Поток

180

EdS Er 2πrh,

заряд, охваченный поверхностью S, q

τh

(см. ЗАДАЧУ О ПОЛЕ ТОНКОЙ ДЛИННОЙ

НИТИ). Получим

2πrh τh

2πε r

Напряжение на обкладках конденсатора

τ dr

U φ φ φ R1 φ R2 1

Erdr 1

2πε r

2πε

Ёмкость, приходящаяся на отрезок кабеля единичной длины,

C		τ	2πε
C		U		0
				0
	1		ln	R
	1
				2
				2
				R
				1

3) Расчёт ёмкости сферического конденсатора с двухслойным диэлектриком

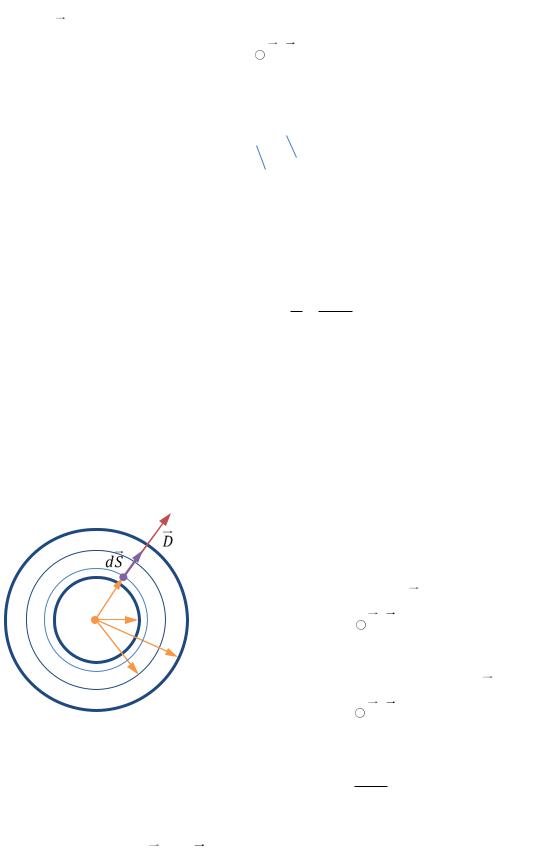
Имеется сферический конденсатор, радиус внутренней обкладки которого равен R1, радиус внешней обкладки – R2, заполненный двумя слоями диэлектрика: диэлектрик с относительной диэлектрической проницаемостью ε1 (область I на РИС. 22.9) примыкает вплотную к внутренней обкладке, диэлектрик с относительной диэлектрической проницаемостью ε2 (область II) – к внешней обкладке, радиус границы разделал диэлектриков равен R0. Найти ёмкость конденсатора.

						Зарядим конденсатор: пусть внутренняя обкладка
						имеет заряд Q, а внешняя обкладка – заряд –Q. Элек-
ε2 ε1					–Q	трическое поле существует только		в пространстве
					–Q	между обкладками (R1 < r < R2). Применим теорему


		r	R1			Остроградского-Гаусса для D
I	Q	O	R1			DdS q .
I				R2		DdS q .
		R0		R2			S
							S
						S
						S
II						Выберем поверхность интегрирования S в виде сферы,
						концентричной конденсатору. Поток		D

Рис. 22.9

	DdS Dr 4πr	2	,
		2

S

охваченный поверхностью S свободный заряд равен Q,

Dr 4πr2 Q

D	Q
		2
r	4πr

Связь между напряжённостью электрического поля и электрическим смещением

D ε εE E		Dr		c , E		Dr		Q		.
0	Ir	ε ε			IIr	ε ε		4πε ε r2
		0	1			0	2	0	2

Напряжение на обкладках конденсатора

181

									R							R						R								R					Q				dr		R	Q		dr
		φ R		φ R					1							0							1								0				Q				dr		1	Q		dr
U φ	φ	φ R		φ R							E		dr				E	IIr	dr					E		Ir	dr													2					2
			1		2							r						IIr								Ir						4πε ε							r	2		4πε ε		r	2
									R							R						R								R		4πε ε							r		R	4πε ε		r
									R							R						R								R						0	2				R	0	1
									2							2							0								2										0
						R						R
				Q	1	0			1				1			Q				1						1				1							1
				Q	1				1							Q				1						1				1							1
			4πε		ε r			ε r							4πε				ε R						ε R				ε R							ε R
			4πε		ε r	2		ε r					0		4πε				ε R						ε R				ε R							ε R
				0	2	2			1				0				0			2	0					2	2		1			1				1		0
				0	2	R			1			R					0			2	0					2	2		1			1				1		0
						Q			ε R R ε R R ε R R ε R R																								.
											1	1		2	1		0	1			2		0			2		2	1		2		.
											1	1		2	1		0	1			2		0			2		2	1		2
						4πε										ε ε R R R
							0										1	2		0	1		2
Ёмкость конденсатора
						Q									4πε0ε1ε2R0R1R2
					C U																													.
					C U					ε R R ε R R ε R R ε R R																								.
											1		1	2		1	0		1		2			0		2		2	1			2

При ε1 = ε2 = ε этот результат переходит в формулу, приведённую в ТАБЛ. 22.1.

182

Лекция 23

3.4.4. Соединения конденсаторов

1. Последовательное соединение

Последовательное соединение конденсаторов – соединение, при котором конденсаторы соединяются разноимённо заряженными обкладками.

На РИС. 23.1 изображена схема батареи из N конденса-

торов, соединённых последовательно. Заряд каждого

конденсатора равен заряду всей батареи, так как все

Рис. 23.1

обкладки кроме крайних (левая обкладка конденсато-

ра С1 и правая обкладка CN на схеме РИС. 23.1) изолированы и сумма их зарядов равна нулю:

Q	Q	Q
1	2	i
Напряжение на i-м конденсаторе

	U	Q
	U	i
		i
	i	C
		C
		i

Напряжение на батарее есть сумма напряжений на каждом из конденсаторов:

U		i					Q
		i					i
			U

							C
							i
Ёмкость батареи
C	Q			1
C	U				1
	U				1
					C
					C
						i

2. Параллельное соединение

Q		1	.
Q	C		.
	C
		i

1		1
C		C
C		C
		i

Рис. 23.2

Параллельное соединение конденсаторов – соединение, при котором конденсаторы соединяются одноимённо заряженными обкладками.

На РИС. 23.2 изображена схема батареи N конденсаторов, соединённых параллельно. Напряжение на каждом из конденсаторов одинаково и равно напряжению на всей батарее:

U1 U2

UN U .

Заряд батареи равен сумме зарядов каждого из конденсаторов:

Q Qi CiUi U Ci .

Ёмкость батареи
	Q	Ci ,
C	Q		C	C	.
			C	C
	U			i
	U

Нужно соблюдать правила построения электрических схем!

183

3.5. Энергия электростатического поля

3.5.1. Энергия заряженного конденсатора

Пусть конденсатор ёмкостью C имеет заряд q. Перенесём положительный малый заряд dq с отрицательно заряженной обкладки на положительно заряженную (РИС. 23.3). При этом внешними силами совершается работа

*	dq φ φ Udq	q	dq .
δA		C

Работа внешних сил по зарядке конденсатора от 0 до Q

		Q	qdq	Q	2
			qdq	Q
A	*			.
	*
		0	C	2C
		0

Так как работа – мера изменения энергии, W = A*,

W	Q	2	CU	2	QU

	2C		2		2

(по определению ёмкости Q = CU). Демонстрация: Энергия конденсатора

q –q dq

Рис. 23.3

3.5.2. Объёмная плотность энергии электрического поля

Q		–Q	Рассмотрим заряженный плоский конденсатор (РИС. 23.4); заряд

			конденсатора равен Q, площадь обкладок – S, расстояние между об-
			кладками – d, конденсатор заполнен диэлектриком с относитель-
			ной диэлектрической проницаемостью ε. Электрическое поле
	d		внутри конденсатора однородно,	его напряжённость равна E . Ём-
			кость этого конденсатора C ε0εS	, а напряжение между обкладка-
Рис. 23.4			кость этого конденсатора C ε0εS	, а напряжение между обкладка-
Рис. 23.4			d

ми (по интегральной связи напряжённости и потенциала) U = Ed. Энергия конденсатора

	CU	2	ε εS			2
W	CU		ε εS	E d	2	ε εE V
W			0	E d		0
			0	2		0
	2		2d			2

где V = Sd – объём конденсатора.

(23.1)

Объёмная плотность энергии электрического поля – энергетическая характеристика поля, равная энергии поля в единичном объёме

	w		W
	w		V
			V
для однородного поля,

	w	dW		;
	w		dV


w			Дж	.
w			3	.
			м

для неоднородного поля.

В изотропной среде с относительной диэлектрической проницаемостью ε

(23.2)

184

w	ε εE	2
	ε εE
	0
	0
	2

Доказательство

Пусть в пространстве существует электростатиче-									φ + dφ
ское поле. Разобьём пространство, на					плоские				φ + dφ
ское поле. Разобьём пространство, на					плоские				φ
конденсаторы: вдоль любой пары близко распо-									φ
конденсаторы: вдоль любой пары близко распо-
ложенных друг к другу эквипотенциальных по-
верхностей можно мысленно разместить тонкие
проводники, которые служат обкладками плоско-
го конденсатора (РИС. 23.5) (при этом поле не ис-
казится, так как проводник в электростатическом
поле эквипотенциален). По формулам					(23.1)			и	Рис. 23.5
(23.2) объёмная плотность энергии									Рис. 23.5
(23.2) объёмная плотность энергии
w	W			ε εE		2
	W			ε εE
				0			, ч. т. д.
				0
	V				2
Так как в изотропной среде D ε0εE ,
w		ε εE E					DE	.
w		0						.
		0
				2			2
Выражение объёмной плотности энергии электрического поля

			w		DE
			w		2
					2

справедливо для любой среды.

Согласно определению объёмной плотности, энергия электрического поля в объёме V

W wdV		DE	dV
W wdV		2	dV
V	V	2
V	V

ПРИМЕР

Энергия электрического поля заряженной сферы

По сфере радиуса R, находящейся в безграничном однородном диэлектрике относительной диэлектрической проницаемостью ε, равномерно распределён заряд Q (РИС. 23.6). Найти энергию электрического поля в сферическом слое, внутренний радиус которого равен r1, а внешний – r2 (r1, r2 > R), концентричном заряженной сфере, и энергию ε электрического поля во всём пространстве.

Сначала нужно найти напряжённость электрического поля. Аналогичная задача (при ε = 1) была решена нами ранее (см. ПРИМЕР 1) В РАЗДЕЛЕ 3.2.3). Воспользовавшись теоремой Остроградского-

Гаусса для D и связью D и E в изотропном диэлектрике, получим, что при r > R (область I на РИС. 23.6)

O R

Рис. 23.6

EIr

при r < R (область II) EIIr = 0.

185

		Q
		4πε εr	2
			2

		0

В области I объёмная плотность энергии электрического поля

w	r	ε εE
w	r	0
		0
I		2
		2

2	ε εQ		2			Q		2
	ε εQ					Q
Ir	0
Ir	0
	2	2		2	4	2	ε εr		4
	2 16π	ε		ε r		32π	ε εr
		0						0

Разобьём пространство вне заряженной сферы на бесконечно тонкие сферические слои, концентричные заряженной сфере. Энергия электрического поля в слое радиуса r и толщины dr

dW w (r)dV	Q2	4πr2dr	Q2dr	.
dW w (r)dV	32π2ε εr4	4πr2dr	8πε εr2	.
I	32π2ε εr4		8πε εr2
	0	2	0
		2

Энергия поля в сферическом слое радиусами r1 и r2

r2	2		Q	2
W	Q dr		Q
W	8πε εr	2	8πε ε
r	8πε εr		8πε ε
r	0			0
1

Энергия поля во всём пространстве

		2
0		Q dr		2
W		8πε	εr
	R	8πε	εr
	R	0

(внутри заряженной сферы поля нет).

1	r2		Q		2	1	1
1			Q			1	1	.
								.
r r			8πε0ε r1				r2
	1
			Q	2
			Q
		8πε εR
		8πε εR
			0

Заметим, что энергия поля всегда положительна вне зависимости от знака заряда.

3.6. Электрический ток

3.6.1. Электрический ток. Сторонние силы

В непостоянном электрическом поле напряжённость поля внутри проводника E 0 и имеет место электрический ток.

Направление тока – направление упорядоченного движения положительно заряженных частиц.

Сила тока57 – скалярная алгебраическая величина – характеристика тока, равная заряду, проходящему через поперечное сечение проводника в единичный промежуток времени:

	I	dq
	I	dt
		dt

ампер – одна из основных единиц СИ.

; [I] = А,

Знак силы тока определяется тем, совпадает ли направление движения положительных зарядов с выбранным положительным направлением обхода проводящего контура (см. НИЖЕ).

Плотность тока – векторная характеристика тока, по модулю равная заряду, проходящему в единичный промежуток времени через единичный участок попе-

57 Эту величину в электротехнике называют током.

186

речного сечения проводника, а по направлению совпадающая с направлением движения положительных зарядов (РИС. 18.1)58:

	dI	n
	dS	n
	dS

мА2

;

Почему возникает электрический ток? На некотором участке проводника происходит разделение зарядов. Такое разделение не может произойти под действием кулоновского (электростатического) поля; под действием кулоновского поля разделение зарядов, наоборот, исчезает. Разделение зарядов происходит под действием электромагнитных (неэлектростатических) полей; эти поля называют

сторонними силами59.

I уравнение Максвелла:

Edl		B	dS
		t
L	S

при		Edl 0
при		Edl 0
	L

Edl A ,

L q0

;

здесь A – работа электрического поля по перемещению пробного заряда q0 по замкнутому контуру L. Представим напряжённость электрического поля в проводнике как

E E	кул	E	стор

(23.3)

– сумму напряжённостей кулоновского и неэлектростатического полей;

Edl E		кул	E	стор	dl
Edl E			E		dl
L	L

E	кул	dl
E		dl
L

E	стор	dl
E		dl
L

	B	dS
	t
S

								0	1 +		– 2
Теперь рассмотрим незамкнутый контур 1-2, лежащий в									1 +		– 2
проводнике (РИС. 23.7). Интеграл по этому контуру										Рис. 23.7
Edl Eкул E		стор dl Eкулdl Eсторdl								Рис. 23.7
2	2	2			2
1	1	1			1
		2	сторdl;
	φ1	φ2 E	сторdl;
		1

					2		стор
				12		E	стор	dl
				12
				E
					1

58РИСУНОК 18.1 следует нарисовать заново.

59Здесь и далее мы сталкиваемся с исторически сложившейся, но не очень удачной терминологией: сторонние силы – это не силы, а поля, т. е. физические объекты; ЭДС – это не силовая, а энерге-

тическая характеристика поля.

187

– электродвижущая сила (ЭДС) – энергетическая характеристика электромагнитного поля (поля сторонних сил), равная работе сторонних сил по перемещению единичного положительного заряда из начала в конец проводника;

3.6.2. Закон Ома

Большинство проводников подчиняется закону Ома. Экспериментальный60 закон

Ома в дифференциальной форме:

j σE

(23.4)

где σ – удельная электропроводность вещества. Закон Ома справедлив для веществ, в которых концентрация носителей заряда остаётся неизменной.

Удельное электрическое сопротивление вещества

	ρ		1	;
	ρ		σ


См		, [ρ] = Ом·м.
м		, [ρ] = Ом·м.
м

Подставим напряжённость электрического поля в виде (23.3) в закон Ома в форме

(23.4), затем умножим скалярно на элемент тока

j σ E	кул	E	стор

					E	кул	dl	E	стор	dl
jdl σE	кул	dl σE	стор	dl	E		dl	E		dl
jdl σE		dl σE		dl		ρ			ρ
						ρ			ρ

Умножим это выражение на ρ и проинтегрируем по контуру 1-2 (РИС. 23.7):

2		2		кул		2		стор
	ρ jdl		E	кул	dl		E	стор	1	2
									1	2
									dl φ	φ
1		1				1

По определению плотности тока

jdl dI ndl dI dl I dl , dS dS S

E12

(23.5)

где S – площадь сечения проводника в направлении, перпендикулярном плотности тока. Подставим это выражение в (23.5) и проинтегрируем по участку 1-2:

2 ρdl

I 1 S φ1 φ2 E12 .

Интеграл в левой части этого равенства – электрическое сопротивление участка цепи 1-2 – характеристика проводника, зависящая от его формы, размеров и материала:

R
12

С учётом определения (23.6) перепишем

2	ρdl
	ρdl	.
	S	.
1	S
1

(23.5) в виде

(23.6)

60 Этот закон для металлических проводников будет выведен в ПАРАГРАФЕ 6.5.

188

IR	φ	φ	E
12	1	2	12

– обобщённый закон Ома для участка цепи. Здесь:

φ1 – φ2 – разность потенциалов на участке 1-2;

E12 – ЭДС на участке 1-2;

	кул	стор
IR12 U12	A	A	– падение напряжения на участке 1-2.
IR12 U12	12	12	– падение напряжения на участке 1-2.
	12	12
	q	q
	0	0

Демонстрации: 1) Падение потенциала вдоль верёвки 2) Усы Курёпина

(23.7)

3.6.3. Соединения проводников

В этом разделе рассматриваются однородные участки цепи, т. е. такие, в которых неэлектростатические поля не совершают работы (E12 = 0). Закон Ома для одно-

родного участка цепи

IR	U	12
12		12

1. Последовательное соединение (РИС. 23.8)

Для N проводников, тельно

I	1	I	2
	1		2

соединённых последова-

IN I ,

Рис. 23.8

проводников в определённый Для однородного участка IiRi =

так как по закону сохранения заряда заряд, проходящий через любое сечение каждого из

промежуток времени, одинаков.

Ui = φ1i – φ2i; общее падение напряжения

U U	U	U
1	2	i

	i
	U

Сопротивление участка цепи, состоящего из N проводников, соединённых последовательно,

R	U	Ui
R	I		I
	I		I
			R
			R

2. Параллельное соединение (РИС. 23.9)

N Ri

i 1

Ui Ii

	i
	R

;

I1 R1

I I2 R2

Ii Ri

IN RN

Рис. 23.9

В этом случае напряжение на всех проводниках одинаково, а токи суммируются:

U1 U2	Ui	UN U ,
I I1 I2	Ii	IN Ii .

Сопротивление участка цепи, состоящего из N проводников, соединённых параллельно,

189

1	N	1
R		R
R	i 1	R
	i 1	i

3.6.4. Правила Кирхгофа

Приведённые ниже два правила являются выражениями физических законов – закона сохранения электрического заряда и закона Ома – и позволяют рассчитать токи и напряжения на любом участке сколь угодно сложной электрической цепи.

1.Алгебраическая сумма токов в узле электрической цепи равна нулю:

				.
I	i	узел	0	.
I			0

Узел электрической цепи – место (точка на электрической схеме), где соединяются два и более проводников (РИС. 23.10). При записи I правила Кирхгофа втекающие в узел токи считаются положительными, вытекающие

– отрицательными.

I правило Кирхгофа следует из закона сохранения электрического заряда.

2.Сумма падений напряжений на замкнутом участке цепи равна сумме ЭДС на этом участке:

I2 Ii IN

Рис. 23.10

i i		i
I R		E

Доказательство

Применим обобщённый закон Ома (23.7) к каждому из N проводников на замкнутом участке цепи:

IiRi φ1i φ2i Ei .

Просуммируем эти выражения по всему замкнутому участку:

IiRi φ1i φ2i E i , ч. т. д.

0, т. к. контур замкнут Для расчёта токов в цепи произвольно выбирают направления токов в каждом

неразветвлённом участке и направления обхода замкнутых контуров. Составляют систему линейных алгебраических уравнений:

N – 1 уравнений по I правилу Кирхгофа (N – число узлов);

k уравнений по II правилу Кирхгофа (k – число независимых замкнутых контуров, т. е. таких контуров, которые нельзя целиком составить из других рассматриваемых контуров).

Эта система уравнений должна иметь одно и только одно решение.

ПРИМЕР
Расчёт токов в разветвлённой цепи		I1	R1		E1
		I1	R1

					I
Электрическая цепь состоит из трёх источников постоянного		I2	R2		I
тока и трёх однородных проводников (схема цепи на	1	I2	R2		E2	2


РИС. 23.11). Параметры E1, E2, E3, R1, R2, R3 известны. Найти токи
		I3	R3	II
в каждой из ветвей цепи.				II
					E3
					E3
Число узлов в цепи N = 2, число независимых контуров k = 2.
Число узлов в цепи N = 2, число независимых контуров k = 2.		Рис. 23.11
		Рис. 23.11

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 3919 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.03.201590.73 Кб23КоммуникацияЛекция.docx
#
31.03.20153.47 Mб19Конс по УП 2013 (12 лекций).pdf
#
31.03.20154.34 Mб306Конспект лекций (Цифровая техника) 2013.doc
#
13.03.20163.73 Mб233Конспект лекций_ФИЗИКА_2сем.pdf
#
31.03.20151.2 Mб690конспект.pdf
#
31.03.201510.55 Mб94Конспект_ИЭЭ_14.pdf
#
31.03.2015289.21 Кб36КОНСТР_ТР_6.docx
#
21.09.2019767.55 Кб5контролинг_итог.docx
#
23.09.201921.23 Кб5Концепция научного менеджмента.docx
#
31.03.20153.97 Mб12КП2.pdf
#
10.11.201934.66 Кб20кПр 2.docx