Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Конспект_ИЭЭ_14

.pdf

Скачиваний:

Добавлен:

31.03.2015

Размер:

10.55 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 3913 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

120

5. Релятивистский закон сложения скоростей

y	t	y′	t′

Пусть материальная точка M движется

со скоростью u		относительно системы

отсчёта K′ (РИС. 15.3). Найдём её скорость в системе отсчёта K.

По определению, проекции скорости в системе отсчёта K′

	K′
O′	x′
K
O	x
O

Рис. 15.3

наты и скорости в системе отсчёта K′:

	dx		dy		dz	;

ux	dt	, uy	dt	, uz	dt

в системе отсчёта K

ux	dx	, uy	dy	, uz	dz	.
	dt		dt		dt

Выразим эти проекции через коорди-

Итак,

dx vdt

, dy dy ,

dz dz ,

;

dx vdt

, uy

, uz

1 v2

, u

Ускорение не является инвариантом преобразований Лоренца. Формулы для преобразования компонент ускорений можно получить аналогичным образом – исходя из определения и преобразований Лоренца:

adux

xdt

	du
	x
, ax	dt

…

1.13. Релятивистская динамика

1.13.1. Релятивистский импульс

Рассмотрим замкнутую механическую систему – два груза одинаковой массы m0, соединённых пружиной (РИС. 15.4). В системе отсчёта K′ центр масс данной механической системы покоится. В начальном состоянии пружина сжата, затем она

разжимается и грузы движутся со скоростями

u	u
1

и u u .

Должен выполняться закон сохранения импульса: импульс данной замкнутой механической системы должен сохраняться в любой инерциальной системе отсчёта.

121

y′

t′

K′

O′

x′

Рис. 15.4

Определим импульс материальной точки, как в классической механике:

p m0u .

Используя РЕЛЯТИВИСТСКИЙ ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ, получим в системе отсчёта K:

проекция начального импульса системы на ось x

P1x 2m0v

проекция конечного импульса

v u

Видно, что P1x ≠ P2x. Получается., что в системе отсчёта K закон сохранения не выполняется, чего не может быть.

Подберём такое выражение для импульса, чтобы py py . (В классической механи-

ке p		m	dy	; так как dy = dy′, а dt = dt′, при таком определении p	p		.) Возьмём в
	y					y
		0	dt	y

качестве элементарного промежутка времени собственное время dτ = dτ′. Тогда

Но

			2
dτ dt	1	u
dτ dt	1	c	2
			2

	dy	m0	dy	py .

py m0	dτ		dτ

, поэтому

p		m dy		m dy
p		0		0
		0		0
	y	dτ			u
						2
			dt	1	c	2
						2

аналогично

m u		y
0		y
			2
			2
1	u
1	c		2
			2

m0ux

, p

m0uz

;

в векторной форме

122

p	m u
p	0
	0
			2
	1	u
	1	c	2
			2

Запишем это определение в виде, аналогичном формуле классической механики:

p здесь m – релятивистская масса:

mu		,
		,
m
0
			2
1	u
1	c		2
			2

1.13.2. Релятивистское уравнение динамики материальной точки

Если материальная точка изолирована, то её импульс

p mu const . Если на точ-

ку действуют другие объекты, то мера взаимодействия – сила F . Запишем уравнение динамики:

		p F			t
или, подставляя выражение для релятивистского импульса,

	d	m u			F
	dt	0	u		F
		0

				2
		1	c	2
				2

– релятивистское уравнение динамики материальной точки.

Так как F f v,t и ни время, ни скорость не являются инвариантами преобразо-

ваний Лоренца, то и сила не является релятивистским инвариантом. Поэтому полученное уравнение динамики малополезно для решения задач.

1.13.3. Энергия в релятивистской механике

Пусть тело движется под воздействием других объектов, которое описывается

силой F , направленной параллельно перемещению				l	(РИС. 15.5). Тело разгоняет-
ся от начальной скорости u0 0	до скорости u .
				x

O
O
t 0			t 0
x 0			x 0
u 0			u 0
Wк 0		Wк 0
	Рис. 15.5
По теореме об изменении кинетической энергии работа силы F
	A	Wк Wк .

123

Найдём работу и, соответственно, кинетическую энергию тела. Элементарная работа на малом перемещении dl (dl = dx)

δA Fdl

Fdxcos0 Fdx

;

так как из релятивистского уравнения динамики

пульс p mu

δA	d mu	dx ud mu .
	dt

Проинтегрируем это выражение:

dp dt

, релятивистский им-

		u	ud mu u mu												u															c	2	u							m				2u du
к																								2						c									m
к																																								0
A W																mudu mu																								0
A W																mudu mu														2											u
		0													0																	0							1			2
		0													0																	0		c		2
																																		c							c	2
																																										2

										u					u														2						u
													2																	1								2
									1				2														c
					m c			2	1				2														c								c			2
			2		m c					c			2					2		m															c					m c			2
			2			0				c								2																									2
	mu															mu
						2			1 2														0												u							0
																														1							2
																														1					c		2
																																					2
															0
															0
					2				m c		2									2
			m u						m c								m u						m c2 mc2 m c2																					,
				0					0									0					m c2 mc2 m c2																					,
						2								2							2								0												0
						2								2							2
			1		u				1	u							1		u
			1		c	2			1		c			2			1			c	2
						2								2							2


										W mc								2	m c							2		.
										W mc									m c
														к								0
При u << c

									1																							2											2
		W m c					2		1						1 m c							2			1					u					1						m u
		W m c													1 m c										1										1							0
																																										0
			к		0					u										0										2c			2									2
										u																				2c												2
									1			2
									1			2
										c		2
										c

– результат классической механики.

Полная энергия

		2
	W mc		.
			.
Представим
2		W m c			2
W mc		W m c
		к		0
При u = 0 W = W0 = m0c2;
	W m c2
	0	0

– энергия покоя.

Энергия покоя может переходить в другие виды энергии.

124

ПРИМЕРЫ

1) Реакция аннигиляции

При взаимодействии частицы и её античастицы они аннигилируют (взаимно уничтожаются) с образованием фотонов. Например, реакция электрона и позитрона

e


e

2γ ,

m0 = 0

γ – фотон рентгеновского излучения. Массы покоя электрона и позитрона одинаковы (m0), а масса покоя фотона равна нулю. Энергия покоя электрона и позитрона переходит в энергию фотона (энергию электромагнитного поля).

2) Дефект масс

Атомные ядра состоят из нуклонов – протонов и нейтронов (см. РАЗДЕЛ 7.1.1). Массы покоя протона и нейтрона в свободном состоянии соответственно равны mp и mn; масса ядра – mя.

Всегда масса ядра меньше суммы масс составляющих его нуклонов:

m Zm A Z
я	p

здесь Z – число протонов в ядре – заряд ядра, нейтронов в ядре. Разность

A –

массовое число, (A – Z) – число

Zm A Z m m
p	n	я

– дефект масс.

Рассмотрим реакцию синтеза атомного ядра (см. РАЗДЕЛ 7.3.5) – реакцию получе-

ния ядра из отдельных нуклонов. Изменение энергии системы нуклонов

к				0
W W			m c
				2
В замкнутой системе W = 0. Поэтому
Wк c	2	m0
Wк c		m0

	W c
			2
	к
m		W
m			к
			к
0		c	2
		c

1.13.4. Вектор энергии-импульса

В 4-пространстве оперируют физическими величинами – 4-векторами.

4-вектор энергии-импульса

	i	W
	i	c



P		px		.
				.
		p
		p	y
			y
		pz
		pz

Найдём модуль вектора энергии-импульса:

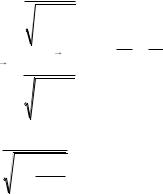
125

W			m c				2
			m c
				0
				0
								2
			1			u
			1				c	2
								2

	p		m u
	p			0
				0
								2
			1			u
			1			c		2
								2

W	m c			2
	m c
		0
		0
	1		c	2	p		2
			c		p
			W			2
						2

p	u		,	u	cp	;
W	c	2		c	W

2	2	2	2	4	inv
W	c p		m c		inv
			0

– модуль вектора энергии-импульса является релятивистским инвариантом.

126

Лекция 16

1.14. Механические колебания40

1.14.1. Виды колебаний

Колебания – периодические изменения какой-либо физической величины во времени. Система тел, в которой происходят колебания, – колебательная си-

стема.

Колебания могут иметь разную физическою природу, но схожее математическое описание. Сейчас мы будем рассматривать механические колебания.

	Колебания
свободные		вынужденные
колебательная система		вынужденные
колебательная система		при периодическом внешнем
предоставлена самой себе		при периодическом внешнем
предоставлена самой себе		воздействии
		воздействии
незатухающие	затухающие
	затухающие

W↓

1.14.2. Свободные незатухающие колебания (собственные колебания)

Рассмотрим свободные колебания пружинного маятника (трения нет) в горизонтальном направлении. Груз – материальная точка массы m – колеблется на пружине жёсткостью k (РИС. 16.1), после того как его вывели из положения равновесия (точка O) и предоставили систему самой себе.

O	x

Запишем II закон Ньютона для груза:	Рис. 16.1
ma Fт N Fупр .

Спроецируем это уравнение на ось x. Так как Fупр x = –kx,

max

По определению, ax d2x2 . Получим дифференциальное уравнение dt

m	d2x	kx 0			d2x
m	dt2	kx 0			dt		2
	dt2				dt		2
Обозначим

			k	ω02		;
			m	ω02		;
			m

		k	x
		m

40 Материал параграфов 1.14 и 1.15 входит в экзаменационную программу II семестра. Материал лекций 16 и 17 может быть, по обстоятельствам, прочитан во II семестре перед темой «ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ» или параллельно материалу этой темы.

127

d	2	x
d		x	2
		2	ω x 0	(16.1)
dt		2	0	(16.1)
dt

– дифференциальное уравнение свободных гармонических колебаний.

Это линейное однородное дифференциальное уравнение второго порядка. Его общее решение41

x t Acos ω0t φ

(16.2)

содержит две произвольные константы A и φ. Данные константы определяются из начальных условий.

Пусть при t = 0 x = x0, vx = 0 (груз оттянули на x0 и отпустили без начальной скорости). Первая производная функции (16.2) – проекция скорости груза на ось x

dx v	x	t Aω sin ω t φ .		(16.3)
dt	x	0	0
dt

Подставим начальные условия в функции (16.2) и (16.3) и найдём константы A и

φ:

x 0			Acosφ,		x	0	Acosφ,
						0
					0		0
							0
v	x	0		Aω sinφ		Aω sin
	x			0

Частное решение дифференциального уравнения условиях



φ

(16.1)

φ 0,
A x	.
0

при данных начальных

x t x	cosω t
0	0
проекции скорости и ускорения на ось x

;

vx t x0ω0 cosω0t , ax t x0ω02 cosω0t .

Графики функций x(t), vx(t), ax(t) представлены на РИС. 16.2. Решение (16.2) – гар-

моническая функция.

В общем решении (16.2):

A – амплитуда колебаний – максимальное отклонение колеблющейся величины от равновесного значения;

ω0 – циклическая частота;

выражение в скобках (аргумент косинуса) – фаза колебаний;

φ – начальная фаза.

Введём другие характеристики гармонических колебаний:

период T – время, за которое колебательная система совершает одно полное колебание;

частота ν – число полных колебаний в единичный промежуток времени;

ω0

2π	,	ν	ω0	1	;
ω	,	ν	2π	T	;
ω			2π	T
0

радс с 1 , ν Гц.

41 Студентам предлагается проверить самостоятельно, является ли формула (16.2) общим решением дифференциального уравнения (16.1).

128

x x0

–x0

x0ω0

–x0ω0

Рис. 16.2

Энергия колебаний (механическая энергия колебательной системы)

W Wк Wп m2v2 kx22 const

(студенты проверяют выполнение этого равенства самостоятельно).

129

Демонстрация: Пружинные маятники

ПРИМЕРЫ

1. Математический маятник

φl

Математический маятник – материальная точка,

подвешенная на невесомой нерастяжимой нити в однородном гравитационном поле.

Найдём период колебаний математического маятника массы m на нити длиной l (РИС. 16.3). Запишем II закон Ньютона:

ma Fт T .

mСпроецируем это уравнение на оси естественной системы координат:

	man T Fт cosφ ,
Рис. 16.3	maτ Fт sinφ .	(16.4)

Груз вращается вокруг оси z по окружности радиуса l. Выразим тангенциальное ускорение маятника через угловое ускорение:

aτ εzl			,
а по определению
ε	z	d2φ .
	z	dt2

Подставим (16.5) и (16.6), а также Fт = mg в уравнение (16.4):

	2
m	d φ			l	mgsinφ
m				l	mgsinφ
	dt		2				,
			2

	2				g
d φ					g	sinφ 0	.
dt		2			l	sinφ 0

При малых углах sin φ ≈ φ и это дифференциальное уравнение примет вид

(16.5)

(16.6)


2	φ
d	φ
dt		2
dt

ω	φ
2
0

– дифференциальное уравнение свободных гармонических колебаний, где

ω0 gl .

Период колебаний математического маятника T 2π ,

ω0

T 2π gl

зависит только от его длины.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 3913 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.03.201590.73 Кб23КоммуникацияЛекция.docx
#
31.03.20153.47 Mб19Конс по УП 2013 (12 лекций).pdf
#
31.03.20154.34 Mб306Конспект лекций (Цифровая техника) 2013.doc
#
13.03.20163.73 Mб233Конспект лекций_ФИЗИКА_2сем.pdf
#
31.03.20151.2 Mб690конспект.pdf
#
31.03.201510.55 Mб94Конспект_ИЭЭ_14.pdf
#
31.03.2015289.21 Кб36КОНСТР_ТР_6.docx
#
21.09.2019767.55 Кб5контролинг_итог.docx
#
23.09.201921.23 Кб5Концепция научного менеджмента.docx
#
31.03.20153.97 Mб12КП2.pdf
#
10.11.201934.66 Кб20кПр 2.docx