Posobie_ch_1

41

для первого варианта перехода в предельное состояние показан на рис. 1.20, б.

Чтобы неизвестное усилие N2 не входило в уравнение, в качестве условия предельного равновесия выберем уравнение "сумма мо-

ментов относительно шарнира A равна нулю" (см. рис. 1.20, б):M A 0 ;

Во втором варианте предельного пластического состояния напряжения в стержнях 2 и 3 равны т, а первый стержень работает в упругой стадии. Планы сил и перемещений показаны на рис. 1.21. За-

Рис. 1.21. Вариант 2 предельного пластического состояния:

а– план перемещений;

б– план сил

Аналогично можно определить предельную нагрузку для третьего варианта, в котором пластически деформироваться будут стержни 1 и 2. Фактической предельной нагрузкой будет минималь-

дает со значением, найденным ранее расчетом по упругопластической стадии.

Надо отметить, что число кинематически возможных вариантов предельного состояния может уменьшиться, если ось какого-либо стержня совпадает с линией действия нагрузки (в этом случае поворота этого стержня не происходит и механизма не образуется).

Допускаемое значение нагрузки определяем как отношение предельного значения нагрузки к коэффициенту запаса прочности n.

IV. Определение остаточных напряжений

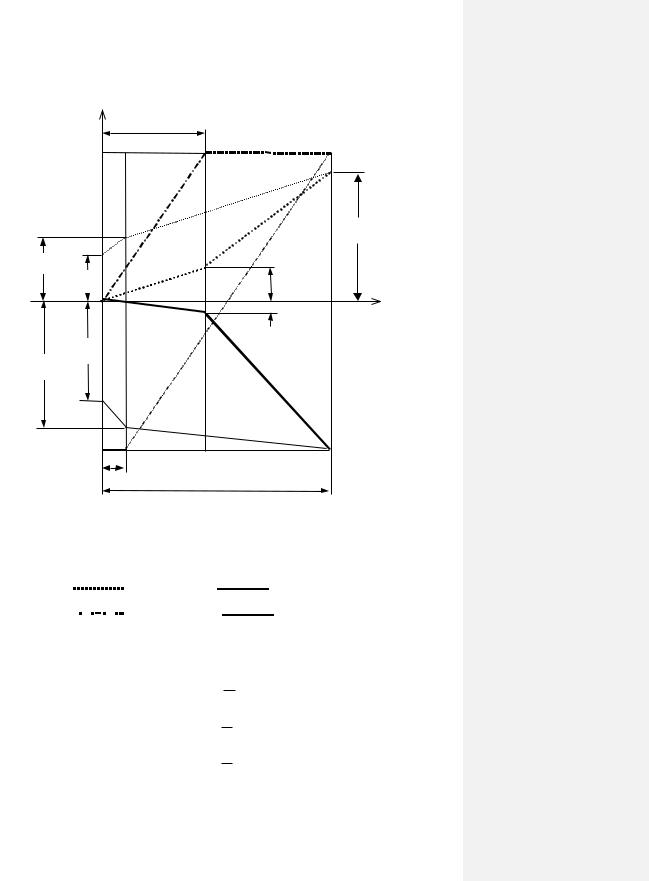
Процесс нагружения конструкции в упругой и упругопластической стадиях, рассмотренный в пп. I и II, можно отобразить на диаграмме в осях F (рис. 1. 22). Характерные точки этой диаграммы получены по соответствующим зависимостям (F ) для трех стержней конструкции.

Рассмотрим процесс полной разгрузки системы из положения предельного равновесия (на диаграмме это соответствует вертикальной прямой с абсцис-

сой Fпплред 1,683 т A). Процесс разгрузки можно трактовать как наложение на

существующие напряжения напряжений от отрицательного приращения нагрузки. Закон изменения последних определяется упругим решением задачи до тех пор, пока величина напряжения в одном из стержней не достигнет т , по-

этому линии разгрузки каждого стержня будут направлены параллельно линиям упругого нагружения (левый участок диаграммы). Если одно из напряжений при разгрузке достигнет величины т (как это имеет место в нашем случае), то

законы изменения напряжений станут соответствовать упругопластической стадии, а их графики будут параллельны соответствующим линиям нагружения (правый участок диаграммы).

Зависимости (F ) можно записать, пользуясь уравнением прямой с известным угловым коэффициентом, проходящей через заданную точку:

0 kA F F0 ,

где k / A угловой коэффициент прямой линии нагружения, параллельной рассматриваемой линии разгрузки; 0 и F0 начальные параметры (напряжение и нагрузка в начале участка). В нашем случае F0 1,683 т A, 0 т для стержней 1 и 3, а для стержня 2 0 0,884 т .

Запишем эти зависимости непосредственно после начала разгрузки:

1 0,101 FA 0,830 т ,

2 0,304 FA 0,372 т ,

3 1,316 FA 1,215 т .

44

Напряжение 3 , как легко вычислить, достигнет значения т при

снижении нагрузки до F 0,163 т A. При этом напряжения в остальных стерж-

нях будут 1 0,846 т , 2 0,422 т .

Пользуясь найденными значениями как начальными параметрами, запишем зависимости для напряжений на втором участке разгрузки, проходящей в упругопластической стадии:

1 FA 0,683 т ,

2 0,707 FA 0,307 т ,

3 т .

При полной разгрузке ( F 0) получаем следующие значения остаточных напряжений: 1 0,683 т , 2 0,307 т , 3 т . В заключение следу-

ет проверить равновесие узла C при полученных значениях остаточных напряжений.

45

2. ИССЛЕДОВАНИЕ ПЛОСКОГО НАПРЯЖЕННОГО СОСТОЯНИЯ. ПРОВЕРКА ПРОЧНОСТИ ДЛЯ СЛОЖНОГО НАПРЯЖЕННОГО СОСТОЯНИЯ

Рекомендуемая литература

Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 13 (§ 13.6).

Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 3 (§ 10, 11), гл. 4 (§ 14, 15, 20).

Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 3 (§ 3.1–3.5, 3.7), гл. 8 (§ 8.1, 8.2).

Основные понятия и формулы

Напряженное состояние в точке тела. Под точкой тела пони-

маем малый объем материала вблизи геометрической точки. Внутри этого объема напряжения изменяются дифференциально мало. На- пряженным состоянием в точке называют совокупность напряжений на всех площадках, проведенных через нее. Напряженное состояние задают три вектора напряжений на трех взаимно перпендикулярных площадках. Эти три площадки выбираются произвольно. Изображают точку в виде параллелепипеда, построенного на указанных трех площадках.

Пусть введена прямоугольная система координат и три площадки, перпендикулярные ее осям x, y, z. Векторы напряжений на этих трех площадках задаются своими проекциями на оси координат и обозначаются соответственно px , p y , p z . Проекции, перпендикуляр-

ные площадкам, называются нормальными напряжениями x , y ,z . Индекс в обозначении указывает направление нормали n к площадке. Проекции, лежащие в плоскостях площадок, называются ка-

сательными напряжениями xy , xz , yx , yz , zx , zy . Первый ин-

декс обозначения определяет площадку, на которой действует напряжение, второй индекс указывает ось, в направлении которой напряжение действует.

Следствием условий равновесия элементарного объема тела яв-

46

ны либо навстречу друг другу, либо в противоположные стороны.

С учетом закона парности касательных напряжений для задания напряженного состояния в точке нужно указать шесть параметров: три нормальных напряжения x , y , z и три касательных напряже-

ния xy , xz , yz .

В точке всегда можно выбрать три взаимно перпендикулярные площадки, на которых действуют только нормальные напряжения, а касательные напряжения равны нулю. Эти площадки называют главными, действующие на них нормальные напряжения – главными на-

пряжениями.

Для главных напряжений, занумерованных по убыванию, используется специальное обозначение: 1, 2 , 3. Обозначение пред-

полагает 1 2 3 (с учетом знака).

Главные напряжения обладают свойством экстремальности: одно из них максимально среди нормальных напряжений на площадках с произвольной нормалью n , другое – минимально. В принятых обозначениях 1 max , 3 min . Пусть pn – вектор напряжения на

площадке с нормалью n , pn – его модуль. Свойство экстремальности означает также следующее: 1 pn 3 .

Главными направлениями напряженного состояния называют направления нормалей к главным площадкам. Эти направления обозначают цифрами 1, 2, 3. Главные площадки обозначают соответст-

венно 1, 2, 3.

Напряженное состояние, при котором ни одно из трех главных напряжений не равно нулю, называется объемным. Если одно из главных напряжений равно нулю, то напряженное состояние называется плоским. При линейном напряженном состоянии отлично от нуля только одно главное напряжение. Далее рассматривается плоское напряженное состояние.

Пусть главная площадка с нулевым главным напряжением расположена перпендикулярно оси y. Тогда при плоском напряженном состоянии отличны от нуля напряжения x , z , xz , zx (рис. 2.1; где

с целью упрощения рисунка напряжения показаны не на всех гранях

47

элементарного параллелепипеда; ненагруженная площадка совпадает с плоскостью чертежа).

Аналитическое исследование плоского напряженного состоя-

ния. Заданы напряжения на взаимно перпендикулярных площадках. Вычисляются напряжения на площадках произвольной ориентации, главные площадки и главные напряжения, площадки, по которым действуют экстремальные касательные напряжения.

Правила знаков для напряжений: нормальное напряжение n

положительно, если направление напряжения совпадает с направлением внешней нормали n (направлено от площадки, растягивающее); касательное напряжение положительно, если в плоскости чертежа оно обходит площадку по часовой стрелке.

На двух взаимно перпендикулярных площадках заданы напря-

zx 0 (обходит площадку против часовой стрелки). При указанном правиле знаков закон парности касательных напряжений имеет вид

Наклонная площадка перпендикулярна чертежу, ее положение определяет угол n между нормалью к ней и осью x (см .рис. 2.2).

Угол n отсчитывается от оси x к нормали n и считается положи-

тельным, если отсчет происходит против часовой стрелки. Нормальное напряжение n и касательное напряжение n на

наклонной площадке определяются формулами

48

нормальное напряжение на площадке, от нормали к которой отсчитан угол n . Касательное напряжение берется с этой же площадки.

Из выражения (2.2а) следует, что сумма нормальных напряжений на двух взаимно перпендикулярных площадках не изменяется

n 90 – нормальное напряжение на площадке, перпендикулярной

площадке с нормалью n.

Когда заданные площадки являются главными, формулы (2.2а) и

Формуле (2.7) отвечает множество углов гл , отличающихся друг от друга на величину, кратную 90 . Разные главные площадки соответ-

ствуют двум из этих углов, которые обозначают , .

гл гл

49

Для определения площадки, на которой действует бóльшее из

напряжений , , нужно вычислить вторую производную

гл гл

– минимальное (с учетом знака) из этих трех напряжений. Максимальное среди касательных напряжений на всевозможных

площадках, проведенных через точку, таково:

1 3 . (2.9)

Это напряжение действует на площадке, одинаково наклоненной к

площадкам 1 и 3. Соответствующее нормальное напряжение

45 1 3 . 2

Касательное напряжение, максимальное по модулю среди напряжений на площадках, перпендикулярных плоскости чертежа, таково:

Графическое исследование плоского напряженного состояния.

Вместо вычислений по приведенным выше формулам можно построить круг напряжений Мора и произвести графические построения. В этом заключается графическое решение задачи (см. примеры).

50

Деформированное состояние в точке. Деформированным со-

стоянием в точке называют совокупность линейных деформаций всевозможных элементарных отрезков, проходящих через точку, и изменений углов между всевозможными парами этих отрезков.

Пусть dx, dy, dz – длины до деформации трех взаимно перпендикулярных элементарных отрезков, расположенных вдоль осей x, y, z . dx , dy , dz – изменения этих длин в результате деформации.

Деформированное состояние в точке определяют шесть пара-

менения прямых углов между отрезками dx, dy, dz .

Через точку всегда можно провести три взаимно перпендикулярных отрезка, углы между которыми не изменятся при деформации. Оси координат, направленные вдоль этих отрезков. называют главными осями деформации.

Связь между напряжениями и деформациями. Для изотропного материала (свойства материала одинаковы во всех направлениях) при не слишком большом уровне напряжений связь напряжений и деформаций описывает обобщенный закон Гука:

Здесь E , G , – упругие характеристики материала. E – модуль Юнга (модуль упругости); – коэффициент Пуассона ( 0 0,5); G – модуль сдвига. Имеет место соотношение G E /[2(1 )] .

Для изотропного материала главные оси деформации и напряженного состояния совпадают, поэтому линейные деформации вдоль