Сферическая функция
В результате
,
(7.24)
.
(7.24а)
Из
(6.120)
следует соотношение между состояниями с противоположными проекциями
.
(7.25)
Используем
,
(1.43)
,
(6.123)
получаем условие ортонормированности
.
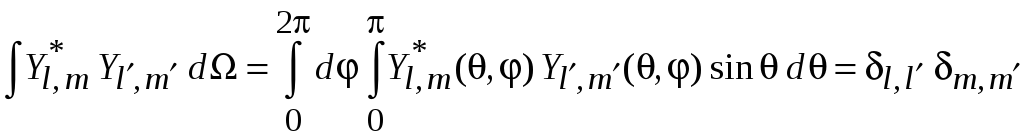(7.27)
Инверсия координат
Заменяем
,
,
,
,
,
,
,
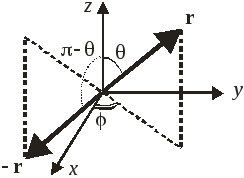
получаем
.
(7.28)
Четность состояния, описываемого сферической функцией, совпадает с четностью орбитального числа l.
Частные выражения
Используем
,
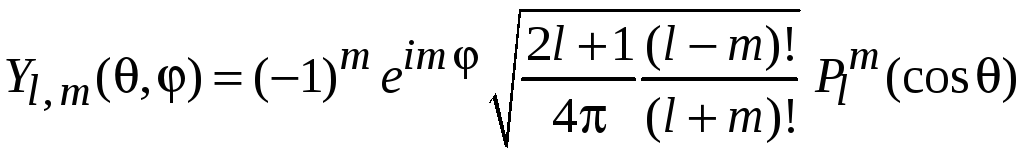(7.24)
и находим
,
,
,
,
,
,
.
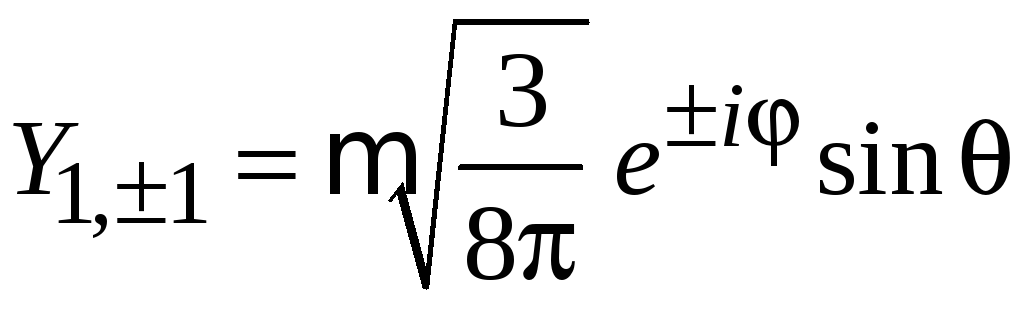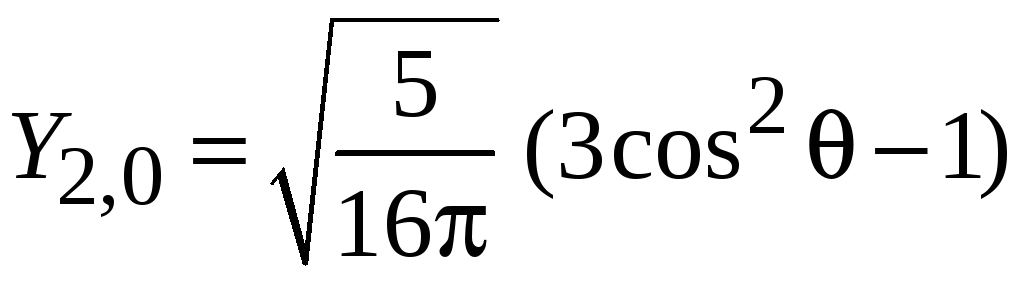(7.29)
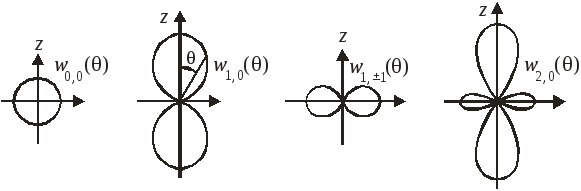
При
нет зависимости от углов –
центрально-симметричное распределение;
При
нет зависимости от угла φ – осесимметричное
распределение.
Плотность вероятности
Вероятность обнаружения состояния в единичном телесном угле
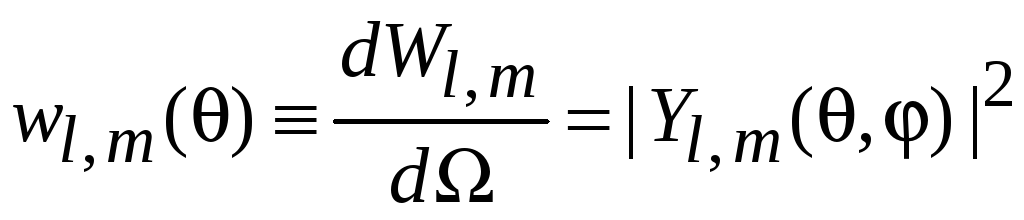
не зависит от φ, т. е. вероятность симметрична при поворотах вокруг оси Оz.
Действие повышающего и понижающего операторов
Используем
,
,
(7.4)
получаем повышающий оператор
.
(7.9)
Действуем им на сферическую функцию
,
(7.22)
получаем
.
С учетом
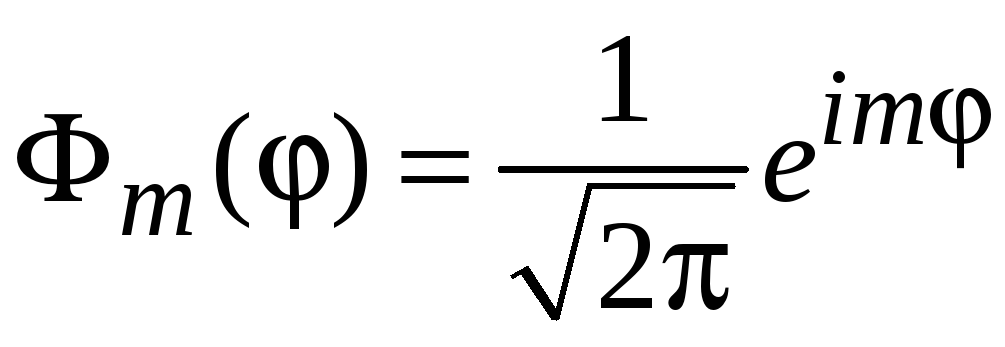
находим
,
.
Используем рекуррентное соотношение
,
(6.141)
тогда
.
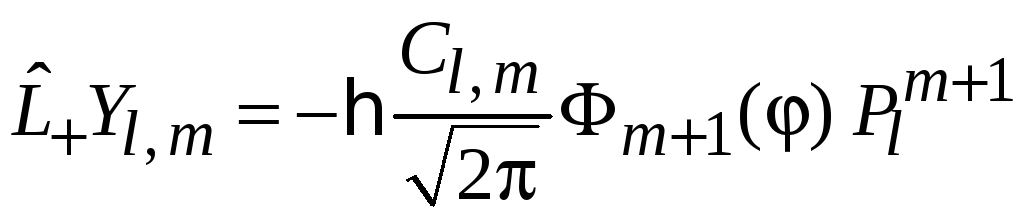Из
.
(7.23)
получаем
.
В результате
.
(7.30)
Также выполняется
.
(7.31)
Доказательство (7.31)
Используем
,
(7.12)
,
,
(7.20)
получаем
.
На
(7.30) действуем оператором
.
Сравниваем правые стороны последних равенств
.
Заменяем
и получаем (7.31).
Рекуррентные соотношения
1. Соотношение
.
(6.127)
умножаем на
,
учитываем
(7.24)
и получаем
.
(7.32)
2.
В (6.125) заменяем
,
тогда
.
Умножаем на
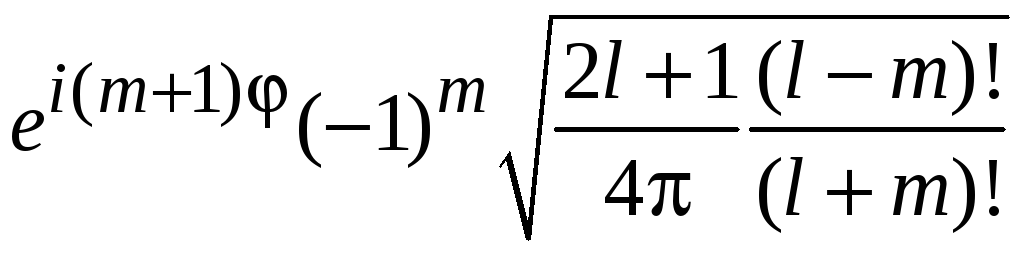
и находим
.
(7.33)
3.
В (7.33) заменяем
,
комплексно
сопрягаем, используем
,
(7.25)
,
получаем
.
(7.34)
Разложение по сферическим функциям
Функцию
на сфере единичного радиуса разлагаем
по базису
.
(7.35)
Для нахождения коэффициентов умножаем разложение (7.35) на
,
интегрируем по углам, используем условие ортонормированности
.
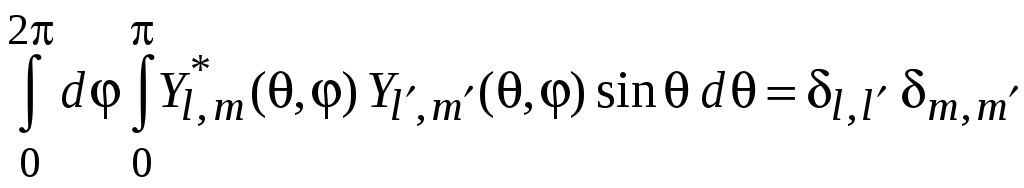(7.27)
Суммы исчезают, находим коэффициент
.
(7.36)
При
осевой симметрии
,
тогда с учетом
.
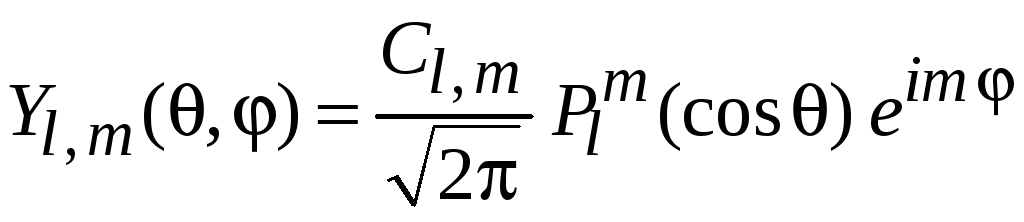(7.22)
из (7.36) получаем
,
где использовано
,
,
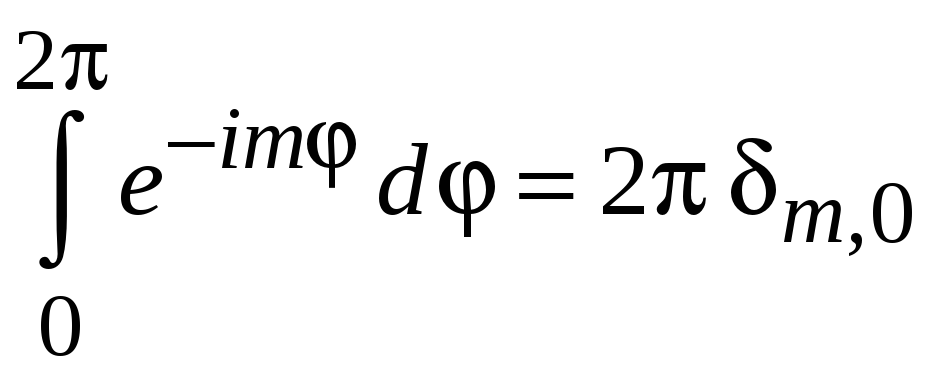тогда
.
Осесимметричная
функция
имеет нулевую проекцию момента импульса,
и разлагается по полиномам Лежандра
,
где
,
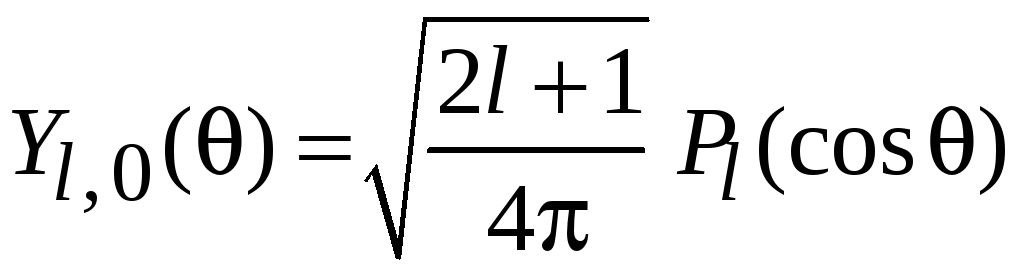(7.24а)
.
Оператор
Лапласа
в цилиндрических координатах
Слагаемые градиента
выражают
быстроту изменения функции, на которую
действует оператор, по направлениям
,
,
.
Элементарные
перемещения при увеличении аргументов
на
равны:
вдоль
получаем
,
вдоль
–
,
вдоль
–
,
тогда
.
Оператор
возводим в квадрат. Используем
,
,
,
,
,
,
и находим
.
Используем
,
,
,
,
и получаем
.
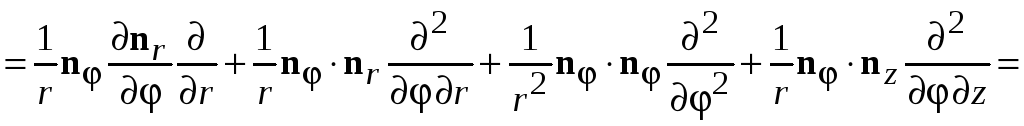
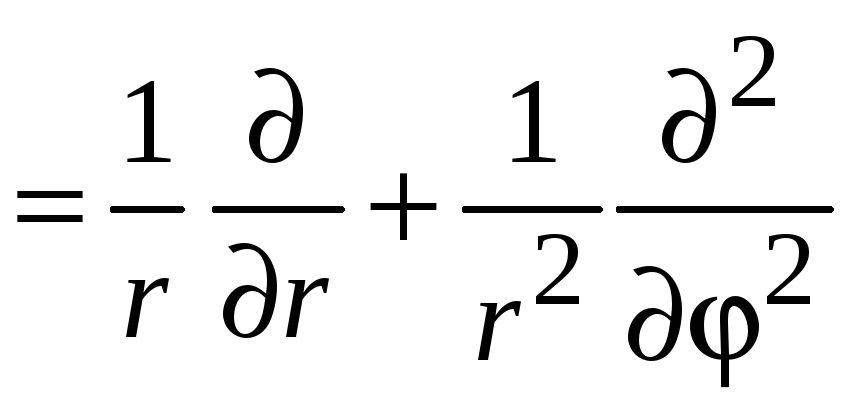Используем
,
,
и находим
.
В результате оператор Лапласа в цилиндрических координатах
.
(П.8.5)
Оператор
Лапласа
в сферических координатах
Элементарные
перемещения при увеличении аргументов
на
:
вдоль
nr
равно
,
вдоль
n
равно
,
вдоль
n
равно
,
тогда
.
(П.8.1)
Возводим (П.8.1) в квадрат.
Первое слагаемое
При изменении радиуса
,
,
,
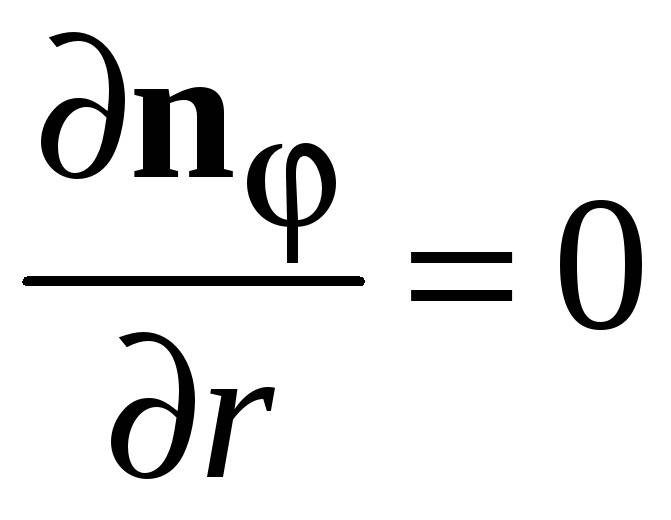тогда
.
Второе слагаемое
При изменении угла θ, аналогично углу φ в полярных координатах:
,
,
,
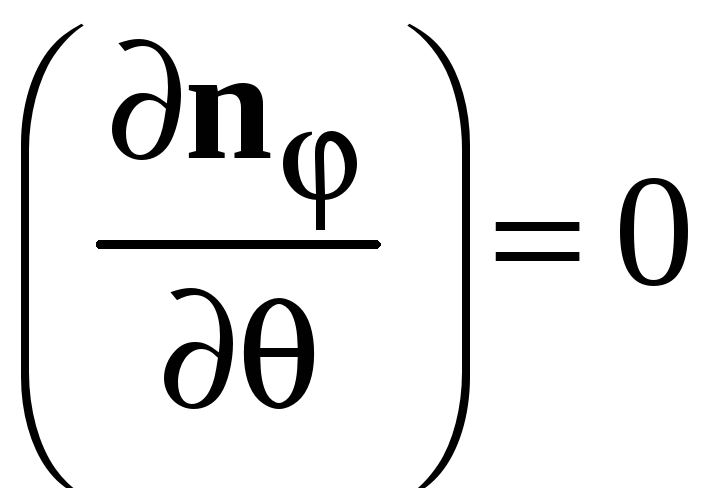тогда
.
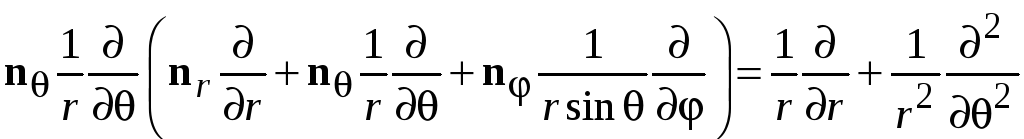Третье слагаемое
При изменении угла φ используем
,
,
,
находим
.
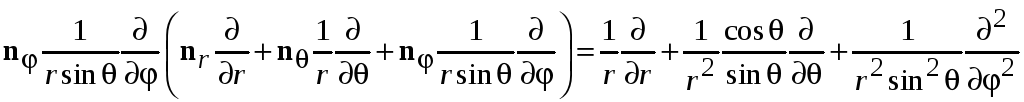В результате оператор Лапласа в сферических координатах
.
(П.8.3)